Wave Frequency And Energy: Exploring The Relationship For Seo

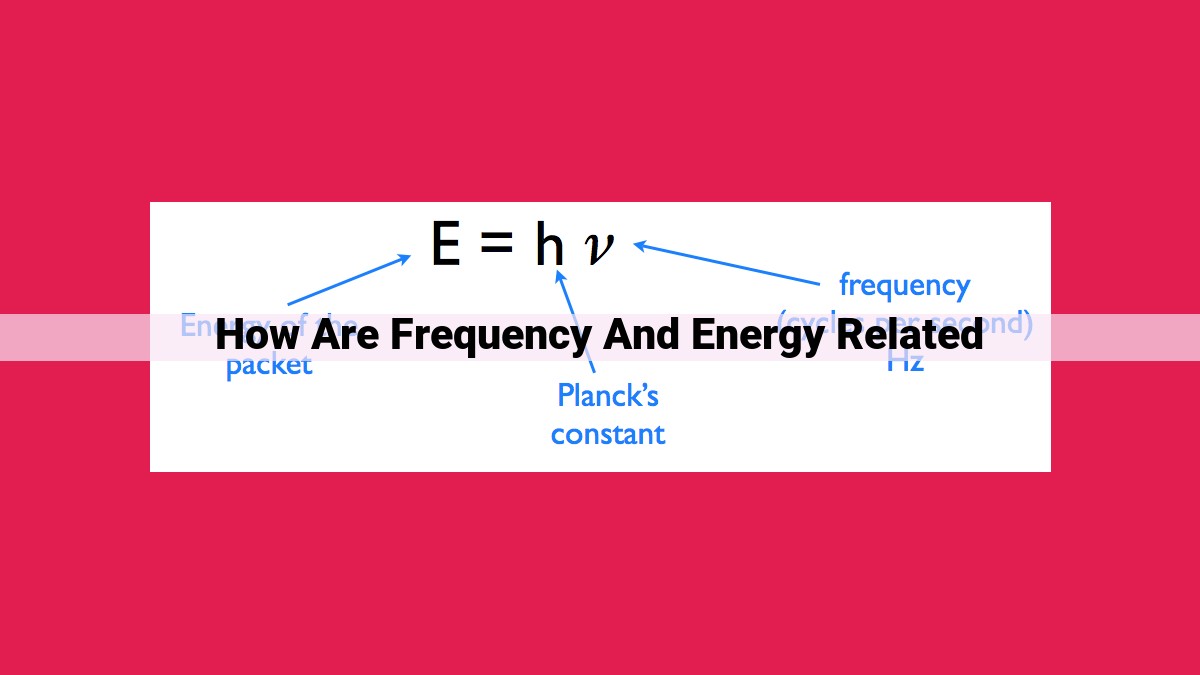
Frequency, measured in Hertz (Hz), represents the number of wave cycles per second. Energy, measured in Joules (J), is the capacity to do work. The frequency and energy of a wave are directly proportional, related by the equation E = hf, where h is Planck’s constant. This means that higher-frequency waves have greater energy, while lower-frequency waves have less energy. Thus, frequency determines the amount of energy carried by a wave, influencing its properties such as wavelength, penetration power, and effect on matter.

Understanding Frequency: The Key to Wave’s Vibrations

In the realm of waves, frequency emerges as a crucial concept, defining the rhythm at which waves dance and oscillate through the expanse. It measures the number of waves that pass a fixed point within a single second. This vibrant dance of waves is measured in units of Hertz (Hz), paying homage to the legendary physicist, Heinrich Hertz, a pioneer in the study of electromagnetic waves.

In this symphony of waves, another two factors emerge—wavelength and amplitude. Wavelength, like a graceful dancer’s stride, denotes the distance between consecutive crests or troughs of a wave. Amplitude, on the other hand, measures the height of a wave’s crest or the depth of its trough, signifying the wave’s energy.

Understanding Energy: The Power Behind Everything

Energy, a concept that permeates our universe, is a fundamental aspect of life. It’s the ability to do work or transfer heat, and it underpins every process that occurs around us.

The unit of energy in the International System of Units (SI) is the Joule (J). Named after the renowned physicist James Prescott Joule, the Joule is used to quantify the amount of work or heat.

Work itself refers to the process of transferring energy from one object to another. Imagine pushing a box across the floor – the effort you put in represents work done. Power, on the other hand, measures the rate at which work is performed, calculated by dividing the amount of work by the time taken.

Unveiling the Harmony of Frequency and Energy

In the realm of physics, understanding the relationship between frequency and energy is crucial for comprehending the intricacies of waves and their behavior in our universe.

Frequency: The Rhythm of Waves

Frequency, denoted by the symbol f, represents the number of oscillations, or cycles, that a wave completes in one second. Measured in Hertz (Hz), which is named after the renowned physicist Heinrich Hertz, frequency quantifies the rate at which these oscillations occur. Frequency is a fundamental characteristic that plays a significant role in defining the properties of waves.

Energy: The Essence of Change

Energy, symbolized by E, is the capacity of a system to perform work or transfer heat. Its unit, the Joule (J), underscores its importance in the context of physics. Energy manifests itself in various forms, including kinetic energy (energy of motion), potential energy (stored energy), and electrical energy.

The Unbreakable Bond: Frequency and Energy

A profound connection exists between frequency and energy. Their relationship is characterized by direct proportionality. This means that as the frequency of a wave increases, its energy also increases. Conversely, a decrease in frequency results in a corresponding decrease in energy. This intricate relationship is aptly expressed by the equation:

E = hf

where h represents Planck’s constant, a fundamental constant in quantum mechanics with the numerical value of 6.626 x 10^-34 J s.

Planck’s Constant: The Quantum Bridge

Planck’s constant serves as a bridge between the macroscopic world of classical physics and the microscopic realm of quantum physics. It acts as a bridge between frequency and energy, and is a fundamental constant of great significance.

This harmonious interplay between frequency and energy is evident in numerous applications. For instance, in the realm of wave properties, frequency dictates the speed, wavelength, and amplitude of waves. High-frequency waves, such as gamma rays and X-rays, possess shorter wavelengths and higher energies compared to low-frequency waves, such as radio waves. This frequency-dependent variation in wave properties has far-reaching implications in fields such as medicine, telecommunications, and astronomy.

Understanding the frequency-energy relationship empowers us to harness the diverse properties of waves for a wide range of applications. From harnessing the energy of high-frequency photons in solar panels to transmitting information via radio waves, the frequency-energy connection plays a pivotal role in shaping our technological advancements.

Planck’s Constant: Unlocking the Secrets of Quantum Mechanics

Imagine yourself as a curious explorer, embarking on a thrilling adventure into the enigmatic realm of quantum mechanics. As you tread through this uncharted territory, you stumble upon a mysterious constant, a guiding light that illuminates the depths of this fascinating world.

This constant, known as Planck’s constant, embodies the essence of quantum mechanics. It represents the cornerstone upon which the entire field rests, providing a profound understanding of the relationship between energy and frequency. Prepare to unravel the secrets of this fundamental constant and its astonishing implications.

Planck’s constant, denoted by the symbol h, is a numerical value that stands at 6.626 x 10^-34 Joule-seconds. This seemingly insignificant number holds the power to unravel the intricate dance between energy and frequency. It defines the relationship between the two quantities, revealing that they are directly proportional.

In the quantum realm, energy comes in discrete packets, known as quanta. The energy of a quantum is directly proportional to its frequency. The higher the frequency, the greater the energy. Planck’s constant represents the conversion factor between these two fundamental properties of light and other quantum particles.

The equation that encapsulates this relationship is E = hf, where E represents energy, h is Planck’s constant, and f is frequency. This equation is a cornerstone of quantum mechanics, providing a pathway to comprehending the enigmatic world of subatomic particles.

Applications: Wave Properties:

• Explain how frequency and energy determine wave properties
• Discuss the relationship between frequency, wavelength, and energy
• Provide examples of different wave properties based on frequency

Applications: Wave Properties

The interplay between frequency and energy doesn’t stop at the theoretical level; it manifests in a myriad of wave properties.

Relationship between Frequency, Wavelength, and Energy

Frequency and wavelength, two fundamental wave characteristics, are inversely proportional. This means that as the frequency increases, the wavelength decreases. Intriguingly, this relationship extends to energy as well. The energy of a wave is directly proportional to its frequency. This can be expressed mathematically as:

E = hf

where E is the energy, h is Planck’s constant, and f is the frequency.

Wave Properties Based on Frequency

The frequency of a wave profoundly influences its properties:

• High-frequency waves, such as X-rays and gamma rays, have shorter wavelengths and higher energies. These waves possess the ability to penetrate matter and are used in medical imaging and cancer treatment.

• Mid-frequency waves, including visible light, have moderate wavelengths and energies. The human eye is sensitive to this range of frequencies, allowing us to perceive colors and shapes.

• Low-frequency waves, such as radio waves, have longer wavelengths and lower energies. They can travel through obstacles and are used in communication and remote sensing.

Understanding the relationship between frequency and energy is essential for comprehending the diverse properties of waves and harnessing their potential in various applications. From medical technology to telecommunications, the frequency of waves plays a critical role in shaping our world.