How To Calculate Voltage Across A Capacitor: A Comprehensive Guide

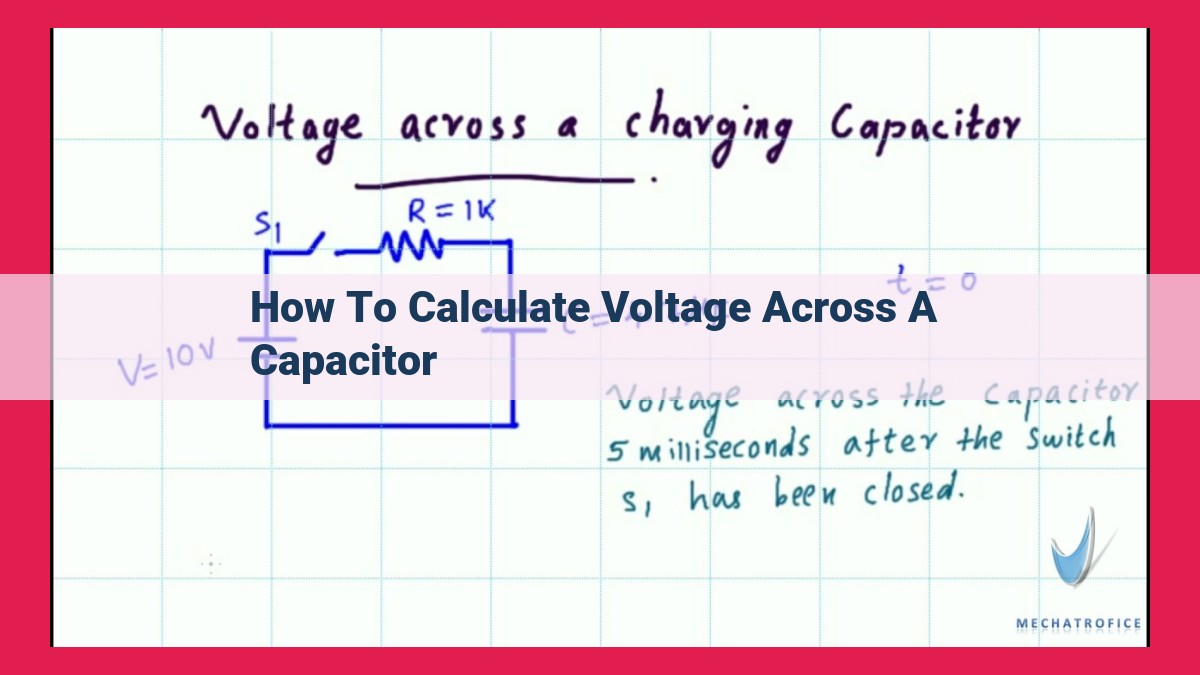
To calculate the voltage across a capacitor, we utilize the formula V = Q/C, where V represents the voltage in volts, Q is the charge stored on the capacitor in coulombs, and C is the capacitance in farads. This equation establishes the relationship between the voltage, charge, and capacitance of the capacitor. By plugging in the known values of charge and capacitance, we can determine the voltage across the capacitor. The SI unit of voltage is the volt (V), charge is the coulomb (C), and capacitance is the farad (F).

Capacitance: The Foundation of Electrical Energy Storage

Imagine electrical energy as a precious treasure that you want to safely store away for future use. Capacitance is the magical property that allows us to do just that. It’s like a tiny vault that can hold onto electrical charge, the fundamental building blocks of electricity.

When a capacitor is connected to a potential difference (voltage), it creates an electric field within its dielectric material. This field acts as a barrier, preventing the charge from escaping. As a result, the charge is stored within the capacitor, like a precious gem tucked away in a secure vault.

The ability of a capacitor to store charge is measured by its capacitance. The higher the capacitance, the more charge it can hold. It’s like having a bigger vault that can accommodate more treasure.

The relationship between capacitance (C), charge (Q), and potential difference (V) is described by the equation:

C = Q / V

This formula tells us that capacitance is directly proportional to charge and inversely proportional to voltage. As you increase the charge, the capacitance increases. However, as you increase the voltage, the capacitance decreases.

Understanding capacitance is crucial for harnessing the power of electricity. It enables us to create energy storage devices like capacitors, which play a vital role in electronic circuits and power systems.

Charge: The Engine Behind Electric Fields

In the realm of electricity, charge plays a pivotal role, acting as the driving force that creates the invisible electric fields that shape the behavior of electrons. Picture a lonely electron floating in space, possessing an inherent negative charge like a tiny magnet. This charge endows the electron with the power to exert an influence on its surroundings, attracting positively charged particles and repelling negatively charged ones.

Imagine a scenario where we gather a multitude of these charged particles and confine them within the confines of a capacitor, a device designed to store electrical energy. Inside this miniature energy vault, a fascinating dance unfolds. Positive and negative charges align themselves on opposite sides of a non-conducting material, creating a potent electrostatic field between them. This field, like an invisible force field, exerts a push-pull effect on other charges in its vicinity, guiding their movement and influencing the flow of electricity.

The magnitude of charge stored on a capacitor’s plates directly governs the strength of the electric field it produces. The greater the charge, the more intense the field becomes, amplifying its ability to influence the behavior of electrons. This fundamental relationship between charge and electric fields is the very essence of capacitor operation, making them indispensable components in a wide range of electronic devices.

Potential Difference: The Driving Force Behind Charge Flow

In the realm of electricity, potential difference reigns supreme as the driving force that propels the flow of charge. Just as a difference in height between two points creates a gravitational force that causes water to flow downhill, a potential difference between two points in an electrical circuit creates an electric field that drives charge carriers to move.

Imagine a capacitor, a deceptively simple device consisting of two conductive plates separated by an insulating material. When we connect a voltage source to the capacitor, a potential difference is established between the plates. This potential difference creates an electric field between the plates, which in turn exerts a force on the charged particles present within the capacitor.

The magnitude of the electric field is directly proportional to the potential difference between the plates. This means that a higher potential difference results in a stronger electric field, which in turn exerts a greater force on the charged particles. Consequently, the charged particles accelerate towards the oppositely charged plate, creating a flow of charge.

The direction of charge flow is determined by the polarity of the potential difference. If the positive plate is at a higher potential than the negative plate, positive charges will flow towards the negative plate, while negative charges will flow towards the positive plate. This flow of charge continues until the potential difference between the plates is neutralized.

Thus, potential difference plays a pivotal role in understanding the behavior of capacitors. It is the driving force behind charge flow, which is essential for the storage and release of electrical energy. Without potential difference, capacitors would be nothing more than inert components, incapable of performing their intended functions in countless electronic circuits.

Capacitor Formula: Unlocking the Voltage

• Present the capacitor formula and its derivation
• Explain how to use the formula to calculate voltage across a capacitor

Capacitor Formula: Unraveling the Voltage Mystery

Capacitors, the unsung heroes of electrical engineering, play a pivotal role in storing electrical energy and influencing the flow of current. Understanding their behavior requires a closer look at the capacitor formula, a key tool for deciphering the electrical realm.

The capacitor formula, V = Q/C, is a straightforward equation that unlocks the secrets of voltage across a capacitor. Voltage (V), measured in volts, represents the electrical potential difference between two points. Charge (Q), measured in coulombs, quantifies the amount of electrical charge stored on the capacitor. Finally, capacitance (C), measured in farads, determines a capacitor’s ability to hold charge.

To derive the capacitor formula, we start with the fundamental definition of capacitance: the ratio of charge stored to the resulting voltage. Rearranging the equation, we get Q = CV. This equation reveals the proportional relationship between charge and voltage. As the voltage across a capacitor increases, the charge stored on it also increases proportionally.

Applying Ohm’s law, which states that voltage is equal to current times resistance, we can modify our equation to Q = V * C, where C is the capacitance. Solving for voltage, we finally arrive at the capacitor formula: V = Q/C.

This formula empowers us to calculate the voltage across a capacitor given its charge and capacitance. For instance, a capacitor with a capacitance of 100 microfarads (μF) and a charge of 0.01 coulombs (C) would have a voltage of 100 volts.

So, the next time you encounter a capacitor in an electrical circuit, remember the capacitor formula as the key to unlocking the voltage mystery. It is a fundamental tool that helps us understand and harness the power of electrical energy.

Units and Consistency: Ensuring Precise Electrical Measurements

When delving into the realm of electrical circuits, it’s imperative to delve into the world of units and consistency, an aspect crucial to ensuring accurate measurements. The International System of Units (SI), a standardized system, plays a pivotal role in this regard, fostering coherence and precision in electrical calculations.

Within the realm of electrical measurements, several fundamental units hold paramount importance:

• Voltage (V): Measured in volts, voltage represents the electrical potential difference between two points, driving the flow of electrons and creating electric fields.

• Charge (C): Measured in coulombs, charge quantifies the amount of electrical charge present, either positive or negative, within a capacitor or any other electrical system.

• Capacitance (F): Measured in farads, capacitance gauges the ability of a capacitor to store electrical charge. It underscores the capacitor’s capacity to accumulate and hold electrical energy.

The formula for capacitance, a cornerstone of electrical calculations, serves as a bridge between these fundamental units:

Capacitance (C) = Charge (Q) / Voltage (V)

This formula provides a direct relationship between the three units, allowing us to determine any one of them given the values of the other two.

Adhering to the SI system ensures consistency in electrical measurements, enabling us to compare and contrast results across different experiments, simulations, and practical applications. Embracing standardized units fosters clarity, precision, and universality in the field of electrical engineering, allowing for effective collaboration and advancement.