Vertex: A Key Feature Distinguishing Cones In Geometry

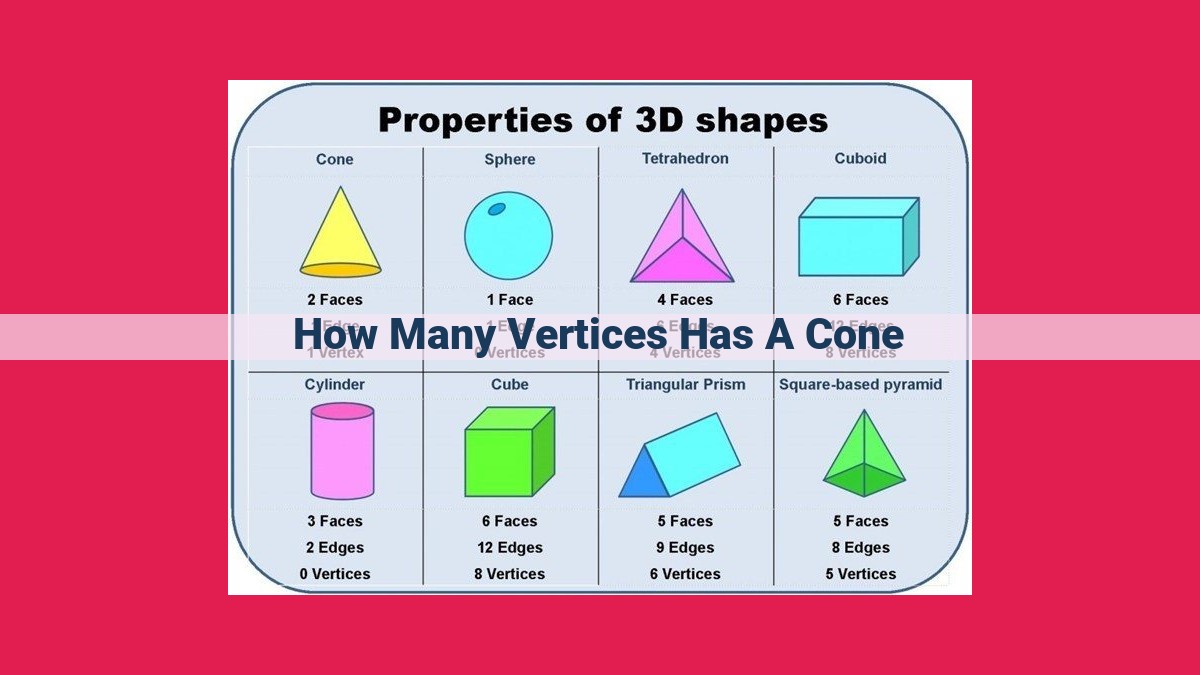
A cone, similar to a pyramid, has only one vertex, which is the point where all the lateral faces converge. This single vertex is a crucial feature that distinguishes a cone from other geometric shapes with multiple vertices, such as cubes or prisms. Understanding the concept of a vertex helps in visualizing and analyzing the cone’s structure and properties.

Understanding the Concept of a Cone

In the realm of geometry, the cone stands as a captivating shape, inviting us to unravel its mysteries. To embark on this journey, let’s begin with a definition of a cone: a three-dimensional figure with a circular base and a single vertex, where its sides taper to a point.

At the heart of a cone lies its key elements. The base forms a circle, characterized by its radius, diameter, and circumference. Extending from the base is the slant height, the distance from the vertex to any point on the edge of the base. This slant height plays a crucial role in determining the height, radius, and lateral surface area of the cone.

The volume of a cone, the amount of space it occupies, is calculated using the formula (1/3)πr²h, where r represents the radius of the base and h represents the height of the cone. Meanwhile, the surface area, which measures the total area of the cone’s surfaces, is computed using the formula πr² + πrs, where s denotes the slant height.

As we delve deeper into the cone’s geometry, we encounter its cross-sections. When a cone is intersected by a plane, the resulting shape can vary depending on the angle of the cut. These cross-sections can take the form of circles, ellipses, parabolas, or even hyperbolas.

The Base of a Cone: Unraveling the Circle Connection

Understanding the Essence of a Cone’s Base

The base of a cone, a pivotal element of this intriguing 3D shape, bears a profound relationship with the concept of a circle. This circular foundation serves as a launchpad for understanding the cone’s other attributes, including its height, volume, and surface area.

Radius, Diameter, and Circumference: A Trio of Measurements

Like a circle, the cone’s base is characterized by a radius, which represents the distance from the center to any point on the base’s circumference. The diameter, twice the radius, measures the length of the base’s longest chord. These measurements establish a baseline for exploring the cone’s dimensions.

Circumference: Encircling the Base

The circumference, a familiar concept from circles, measures the perimeter of the base. It determines the total length around the edge of the circle. This vital parameter reveals the extent of the base’s curvature and its impact on the cone’s overall structure.

Intersecting the Cone: Unveiling Hidden Shapes

When a cone is sliced perpendicularly through its base, the resulting cross-section is a circle. This perfect shape mirrors the base’s circular form, reinforcing the cone’s connection to circles.

The base of a cone, with its inherent circularity, lays the foundation for understanding the cone’s geometry and measurements. Through its radius, diameter, and circumference, the base establishes a framework for unraveling the mysteries of this fascinating shape. Whether it’s calculating volume, surface area, or exploring cross-sections, the base serves as a pivotal reference point, solidifying the cone’s unique characteristics.

Slant Height: The Essential Dimension of a Cone

In the realm of geometry, the cone stands tall as a captivating figure. Its unique shape, characterized by a circular base and a conical surface, has fascinated mathematicians and artists alike for centuries. Among its defining features, the slant height emerges as a crucial component that unveils the cone’s secrets.

What is the Slant Height of a Cone?

The slant height of a cone, often denoted as l, represents the straight-line distance from the vertex (the tip) to any point on the edge of the circular base. This distance plays a pivotal role in defining the cone’s proportions and determining its geometric properties.

Impact on Height, Radius, and Lateral Surface Area

The slant height’s significance extends beyond its mere definition. It establishes an intricate relationship with other key dimensions of the cone:

• Height: The height (h) of a cone is the perpendicular distance from the vertex to the base. It forms a right angle with the radius of the base.
• Radius: The radius (r) of a cone’s base is the distance from the center of the base to any point on its circumference.
• Lateral Surface Area: The lateral surface area (LSA) of a cone is the area of its conical surface, excluding the base.

These three dimensions are interconnected through the slant height:

• The slant height is the hypotenuse of a right triangle formed by the radius, height, and slant height. This relationship is expressed in the Pythagorean theorem: l² = r² + h²
• The lateral surface area of a cone is given by the formula: LSA = πrl

Therefore, the slant height not only measures the distance from the vertex to the base but also serves as a crucial link between the cone’s height, radius, and lateral surface area. Understanding its role is paramount in grasping the geometry of this captivating three-dimensional shape.

Unraveling the Secrets of a Cone: Its Volume Unveiled

In the realm of geometry, we encounter intriguing shapes that captivate our imagination. Among them, the cone stands out with its graceful silhouette and intriguing properties. In this captivating tale, we unravel the mysteries surrounding the volume of a cone, exploring the secrets that lie within its form.

Like a majestic mountain rising from the earth, the cone possesses a circular base, elegantly expanding to form a single vertex. This convergence point, where all the cone’s lines meet, holds the key to unlocking its volume.

To embark on our journey, let us delve into the formula that governs the cone’s volume:

Volume = (1/3)πr²h

In this equation, π (pi) represents the constant value 3.14, r denotes the radius of the cone’s base, and h signifies the height of the cone from its base to the vertex.

The formula suggests that the volume of a cone is directly proportional to the square of its base radius and the height. Simply put, a larger base and a taller height result in an increased volume. This relationship is akin to filling a cone-shaped container with sand or water; more space within the cone leads to a greater amount contained.

Example:

Consider a cone with a base radius of 5 centimeters and a height of 10 centimeters. Plugging these values into the formula, we find the volume:

Volume = (1/3)π × 5² × 10
Volume ≈ 261.80 cubic centimeters

This result reveals that the cone can hold approximately 261.80 cubic centimeters of volume.

Understanding the volume of a cone is not merely an academic exercise. It has far-reaching applications in various fields, such as architecture, engineering, and design. From calculating the capacity of a conical water tank to designing optimal shapes for wind turbines, the concept of cone volume plays a vital role.

Now, with the mystery of cone volume unraveled, we can appreciate the profound impact this geometric wonder has in shaping our world. So, let us venture forth, equipped with this knowledge, and seek out other geometric secrets that await our discovery.

Exploring the Surface Area of a Cone: A Guide for Beginners

In the realm of geometry, the cone stands tall as a fascinating three-dimensional shape with a wealth of intricacies. Among its many attributes, the surface area reigns supreme as a measure of the total area covering its enchanting exterior.

To determine the surface area of a cone, we embark on a mathematical journey involving its radius, height, and the enigmatic constant pi. The formula, a testament to the beauty of geometry, unfurls as:

Surface Area = π * r * (r + l)

Here, the radius r defines the width of the cone’s base, while the height l represents the distance from the base to the tip of the cone. The lateral surface area, a crucial component in this calculation, refers to the area of the cone’s curved surface.

Unraveling the formula, we observe the multiplication of pi by r and the sum of r and l. This intricate interplay highlights the cone’s unique shape, which resembles a pyramid with a circular base. Unlike a pyramid, however, a cone boasts only one vertex, the point where its sloping sides converge.

Understanding the surface area of a cone is a foundational step in the vast world of geometry. This knowledge empowers us to determine the volume of the cone, explore its intersections with other planes, and delve into the fascinating realms of conic sections. As we delve deeper into this geometric wonderland, the surface area of a cone unravels as a gateway to unlocking countless secrets that await our discovery.

Unveiling the Secrets of a Cone: Exploring Its Cross-Sections

When a cone meets a slicing plane, a fascinating dance of geometry unfolds, revealing a kaleidoscope of cross-sectional shapes. Let us embark on a journey to uncover the secrets of these enigmatic intersections.

Circular Cross-Section: A Perfect Alliance

When the slicing plane runs parallel to the base of the cone, a perfect circle emerges. This section captures the essence of the cone’s circular base, mirroring its shape and size. It is a harmonious union, a testament to the cone’s inherent circular symmetry.

Elliptical Cross-Section: An Oval Interplay

As the slicing plane angles away from the parallel, an elliptical cross-section graces our view. This oval-shaped intersection presents a delightful blend of the cone’s base and slant height. Its elongated form eloquently captures the interplay between the cone’s circular base and its rising sides.

Parabolic Cross-Section: A Gateway to Curvature

When the slicing plane strikes the cone obliquely, a captivating parabolic cross-section manifests. This curve, reminiscent of a parabola, embodies the cone’s slant height in its purest form. It showcases the graceful curvature that characterizes the cone’s sides, offering a glimpse into its three-dimensional splendor.

Hyperbolic Cross-Section: Unraveling Infinity

In the realm of geometry, there lies an enigmatic shape known as a hyperbola. When the slicing plane passes through both the vertex and the base of the cone, a hyperbolic cross-section appears. This mesmerizing curve symbolizes infinity, extending indefinitely in both directions. It is a testament to the cone’s ability to transcend the boundaries of conventional geometry.

The cross-sections of a cone are a testament to the captivating interplay of geometry and shape. They unveil the hidden depths of this iconic form, revealing a symphony of circular, elliptical, parabolic, and hyperbolic curves. Whether it be a perfect circle or an enigmatic hyperbola, each cross-section tells a tale of the cone’s inherent geometry and its ability to inspire mathematical marvels.

Comparison to a Pyramid

• Similarities and differences between cones and pyramids, including related geometric shapes

Understanding the Similarities and Differences between Cones and Pyramids

In the realm of geometry, cones and pyramids share certain characteristics, yet they also possess distinct differences. By delving into a comparative analysis, we unravel the intriguing similarities and contrasts that define these two three-dimensional shapes.

Similarities

Cones and pyramids both belong to the family of polyhedra, characterized by their polygonal bases and sloping sides. Their bases are typically square or circular, serving as the foundation upon which these structures are built. Both cones and pyramids possess an apex, the point where their sides converge, forming the shape’s summit.

Differences

The primary distinction lies in the number of sides that connect the base to the apex. A cone has one circular base and a curved surface, reminiscent of a party hat or an ice cream cone. In contrast, a pyramid has a polygonal base with multiple straight edges and a collection of triangular faces that meet at the apex.

Another significant difference is the shape of the cross-section. When a cone is sliced perpendicular to its axis, the resulting cross-section is always a circle. However, the cross-section of a pyramid depends on the orientation of the cut. It can be a triangle, square, or even a more complex polygon.

Related Geometric Shapes

While cones and pyramids share some common features, they also have distinct relationships with other geometric shapes. A cone is closely related to a circle, as its base is a circular region. A pyramid, on the other hand, is associated with triangles, as its sides are triangular faces.

Cones and pyramids, despite their shared classification as three-dimensional polyhedra, exhibit distinct characteristics that set them apart. Their unique base shapes, cross-sectional geometries, and related geometric associations contribute to the fascinating diversity of the geometric landscape. Understanding these differences enables us to appreciate the intricate beauty and versatility of these fundamental geometric forms.

Understanding the Vertex of a Cone

In geometry, understanding the vertices of a cone is crucial. A vertex is the point where multiple edges or faces of a solid figure meet. In the case of a cone, we encounter a unique situation compared to other 3D shapes.

Unlike pyramids, which possess multiple vertices due to their polygonal bases, a cone has only one vertex. This distinctive feature arises from its similarity to a pyramid. Just as a pyramid has a single point of convergence at its apex, so does a cone.

The solitary vertex of a cone resides at the apex of the figure, where the slant height meets the base. This vertex plays a significant role in determining the overall shape and dimensions of the cone. It’s the point from which the lateral surface extends outward, forming the iconic conical shape.

Comprehending the vertex of a cone not only enhances our geometric knowledge but also provides a foundation for exploring more complex concepts in geometry and beyond.