Seo-Optimized Title:unveiling The Secrets Of Velocity-Time Graphs: Understanding Slope And Its Role In Motion Analysis
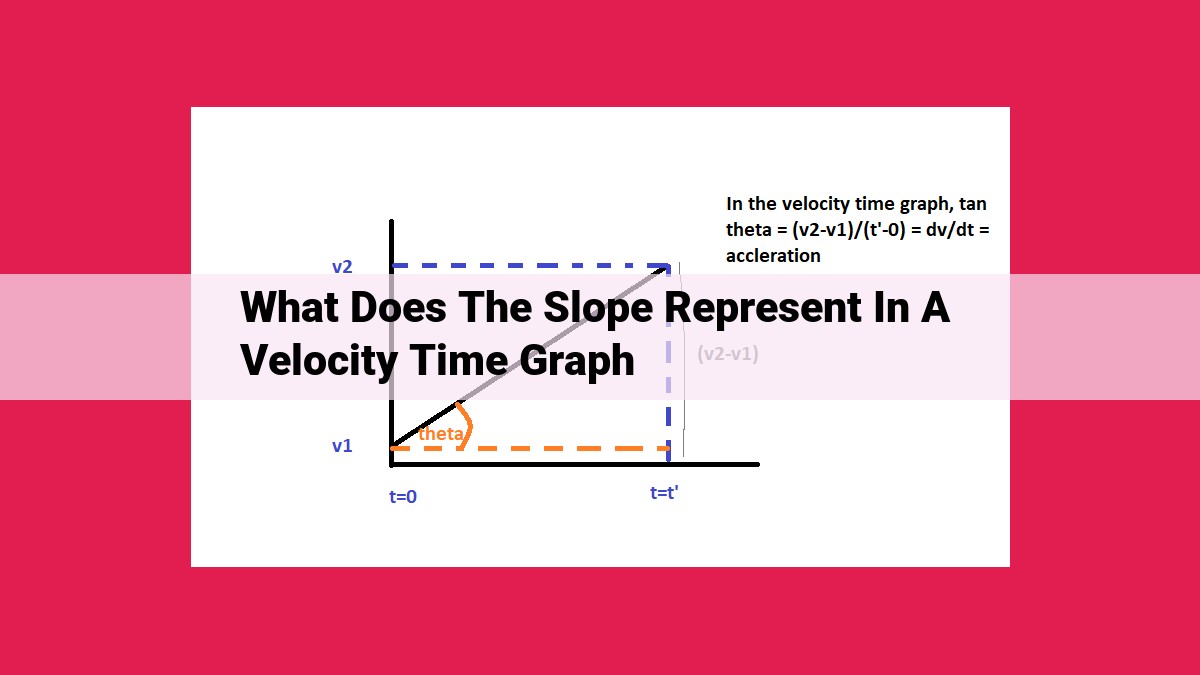
In a velocity-time graph, the slope represents the rate of change of velocity over time, also known as acceleration. The formula for calculating slope is Δv / Δt, where Δv is the change in velocity and Δt is the change in time. The units of slope are typically meters per second per second (m/s^2). A positive slope indicates increasing velocity, a negative slope indicates decreasing velocity, and a slope of zero indicates constant velocity. Zero slope means the object is at rest or moving with constant velocity. The slope of a velocity-time graph can be used to analyze motion, such as determining acceleration, identifying changes in velocity, and calculating displacement.
Understanding Slope: A Guide to Velocity-Time Graphs
In the world of motion, graphs play a crucial role in analyzing how objects move. Among these, velocity-time graphs stand out as invaluable tools for deciphering the changes in speed and velocity of moving objects. The slope of a velocity-time graph is a key element in this analysis, providing a wealth of information about the motion of an object.
What is Slope?
Imagine yourself driving a car at a constant speed on a straight road. As you look at the speedometer, you’ll notice that the needle points to a fixed value, indicating that your *velocity is constant.*
Now, let’s say you decide to accelerate your car. The speedometer needle will start to move, indicating an increase in your velocity. If you were to plot a graph of your velocity against time, you would observe a straight line with an upward slope.
The slope of this line represents the _rate at which your velocity is changing over time_, which is known as *acceleration. The steeper the slope, the greater the acceleration.*
Calculating Slope
To calculate the slope of a velocity-time graph, we use the following formula:
Slope = Δv / Δt
where:
- Δv is the change in velocity (final velocity – initial velocity)
- Δt is the change in time (final time – initial time)
Units of Slope
The units of slope are typically meters per second per second (m/s^2). This unit represents the acceleration of the object, which is the rate at which its velocity changes over time.
Slope Formula
- Provide the formula for calculating slope (Δv / Δt) and explain the meaning of each variable.
Calculating Slope: Unraveling the Secrets of Velocity Change
When it comes to unraveling the dynamics of motion, understanding the concept of slope is crucial. Slope, in the realm of velocity-time graphs, is the keystone to comprehending how objects accelerate or decelerate over time. To unlock this hidden treasure, we delve into the magical formula that quantifies this enigmatic force:
The Enigmatic Slope Formula: A Tale of Velocity and Time
The formula for calculating slope, like a whispered secret, is revealed:
Slope = Δv / Δt
Where:
-
Δv (pronounced “delta v”): This mesmerizing symbol represents the change in velocity, the difference between an object’s initial and final velocities. It’s like the transformation from a caterpillar to a butterfly, a metamorphosis in motion.
-
Δt (pronounced “delta t”): This enchanting variable stands for the change in time, the duration over which the velocity transformation occurs. It’s the journey, not the destination, that matters here.
Delving into the Equation: Unraveling Hidden Relationships
The slope formula is not merely a mathematical equation; it’s a narrative that describes the intricate dance between velocity and time. The slope, measured in units of meters per second per second (m/s²), unveils the rate at which velocity changes with respect to time. It’s the heartbeat of motion, revealing whether an object is accelerating or decelerating.
A positive slope whispers of a positive acceleration, indicating that the object’s velocity is increasing as time progresses. It’s like a rocket soaring upwards, its velocity increasing with each passing second.
Conversely, a negative slope signifies a negative acceleration, a gradual decrease in velocity over time. Imagine a gentle descent, where the object loses speed as it glides towards its destination.
And when the slope vanishes, surrendering to zero, it signifies a state of constant velocity. The object’s velocity remains unchanged, like a steady stream flowing through time.
Understanding the Units of Slope: Meters per Second per Second (m/s²)
The Concept of Slope
In the realm of physics, slope holds a pivotal role in deciphering the dynamics of motion. It represents the rate of change in an object’s velocity over time. Imagine a daring racecar accelerating down a straightaway, with its speedometer needle swiftly climbing. The slope of the velocity-time graph for this car would mirror this increase, revealing the precise rate of acceleration.
The Formula of Slope
To calculate the slope of a velocity-time graph, we employ the formula:
Slope (m) = Change in Velocity (Δv) / Change in Time (Δt)
where Δv signifies the difference between two velocity values and Δt represents the corresponding time interval.
Units of Slope: Meters per Second per Second
The units of slope provide crucial insights into the rate of change being measured. In the context of velocity-time graphs, the units are typically expressed as meters per second per second (m/s²). This unit signifies that for every second that elapses, the velocity of the object changes by a certain number of meters per second.
Importance of Understanding Units
Grasping the units of slope is essential for correctly interpreting velocity-time graphs. For instance, a slope of 5 m/s² indicates that the object’s velocity is increasing by 5 meters per second for every second that passes. Conversely, a slope of -3 m/s² indicates that the object’s velocity is decreasing by 3 meters per second every second.
The units of slope, meters per second per second (m/s²), serve as a critical component in comprehending velocity-time graphs. By deciphering the slope, we gain valuable insights into the rate of change in an object’s motion, empowering us to delve deeper into the fascinating world of physics.
Slope: Understanding the Dynamics of Velocity
In the realm of motion, slope plays a crucial role in unraveling the intricate tapestry of velocity. It embodies the rate of change in velocity over time, providing invaluable insights into the dynamics of an object’s journey.
Positive Slope: A Tale of Accelerating Adventure
When the slope of a velocity-time graph is positive, it signifies an increasing velocity. Picture a car accelerating down a highway, its speedometer steadily climbing. The steeper the upward slope, the greater the acceleration, painting a vivid narrative of growing speed.
Negative Slope: The Gradual Descent of Velocity
Conversely, a negative slope betrays a decreasing velocity. Envision a ball soaring through the air, its upward trajectory gradually succumbing to the relentless pull of gravity. The downward slope portrays the waning speed as the ball gracefully descends.
Zero Slope: A Stasis of Velocity
The enigmatic slope of zero represents a state of constant velocity. Consider a car cruising along a straightaway at a steady pace. Its velocity remains unwavering, frozen in time upon the horizontal plateau of the velocity-time graph. This serene landscape reflects the absence of any velocity change.
Significance of Slope in Motion Analysis
The slope of a velocity-time graph is an invaluable tool for dissecting the intricacies of motion. It enables us to determine acceleration, a measure of how rapidly velocity is changing. A steep positive slope indicates a high acceleration, while a steep negative slope suggests a dramatic deceleration.
Furthermore, slope aids in identifying changes in velocity. Sudden shifts in slope reveal abrupt accelerations or decelerations, painting a clear picture of an object’s velocity variations. By analyzing the slope, we can unravel the story of an object’s velocity profile over time.
Additionally, slope serves as a pivotal factor in calculating displacement, the distance traveled by an object. By integrating the velocity-time graph, we effectively measure the area beneath the curve. The resulting area translates into the object’s displacement, offering a comprehensive understanding of its spatial journey.
Understanding Zero Slope in Velocity-Time Graphs
When analyzing motion using velocity-time graphs, the slope of the line provides valuable insights into the object’s acceleration and changes in velocity. However, a special case arises when the slope is zero.
Zero Slope: A Tale of Constant Velocity or Rest
A zero slope on a velocity-time graph indicates that the velocity of the object is constant or that the object is at rest. In other words, there is no change in velocity over time.
Constant Velocity
If the velocity-time graph is a horizontal line, the slope is zero, which means the velocity is not changing. The object is moving with a constant velocity.
At Rest
If the velocity-time graph is a horizontal line at zero, this indicates that the object is at rest. The object has no velocity, and therefore, the slope is zero.
Implications of Zero Slope
A zero slope on a velocity-time graph has several implications:
- No Acceleration: The object is not accelerating or decelerating because its velocity is not changing.
- Constant Displacement: If the object is not at rest, the constant velocity implies that it is traveling a constant distance in equal intervals of time, resulting in a constant displacement.
- Uniform Motion: The object is in uniform motion, which means it is moving in a straight line with a constant speed.
Understanding zero slope is crucial when analyzing velocity-time graphs to gain insights into an object’s motion. It helps determine whether the object is at rest, moving with constant velocity, or accelerating.
Applications of Slope in Velocity-Time Graphs
Unlocking the secrets of motion with velocity-time graphs, slope emerges as a guiding star, illuminating our understanding of how objects move and interact with the world around us. Embark on a journey through real-world examples, where slope unravels the mysteries of acceleration, velocity changes, and even displacement.
Determining Acceleration:
Imagine a speeding race car zipping across the track. Its velocity-time graph reveals a positive slope, indicating that the car is accelerating. The steeper the slope, the greater the acceleration. Conversely, a negative slope tells us the car is slowing down, or decelerating.
Identifying Velocity Changes:
The velocity-time graph of a bouncing ball illustrates a series of positive and negative slopes. Each change in slope represents a momentary change in velocity. Positive slopes signal increasing velocity as the ball rises, while negative slopes indicate decreasing velocity as it falls.
Calculating Displacement:
The area under a velocity-time graph represents the object’s displacement. Picture a cyclist maintaining a constant velocity for a period of time. The slope of the graph is zero, but the area beneath the line corresponds to the distance traveled by the cyclist.
Slope is an indispensable tool for understanding and interpreting velocity-time graphs. It unlocks the secrets of object motion, from determining acceleration and velocity changes to calculating displacement. Armed with this knowledge, you can now decipher the movements of everything from speedy race cars to bouncing balls, expanding your understanding of the world around you.