Mastering Vector Field Sketching: A Comprehensive Guide

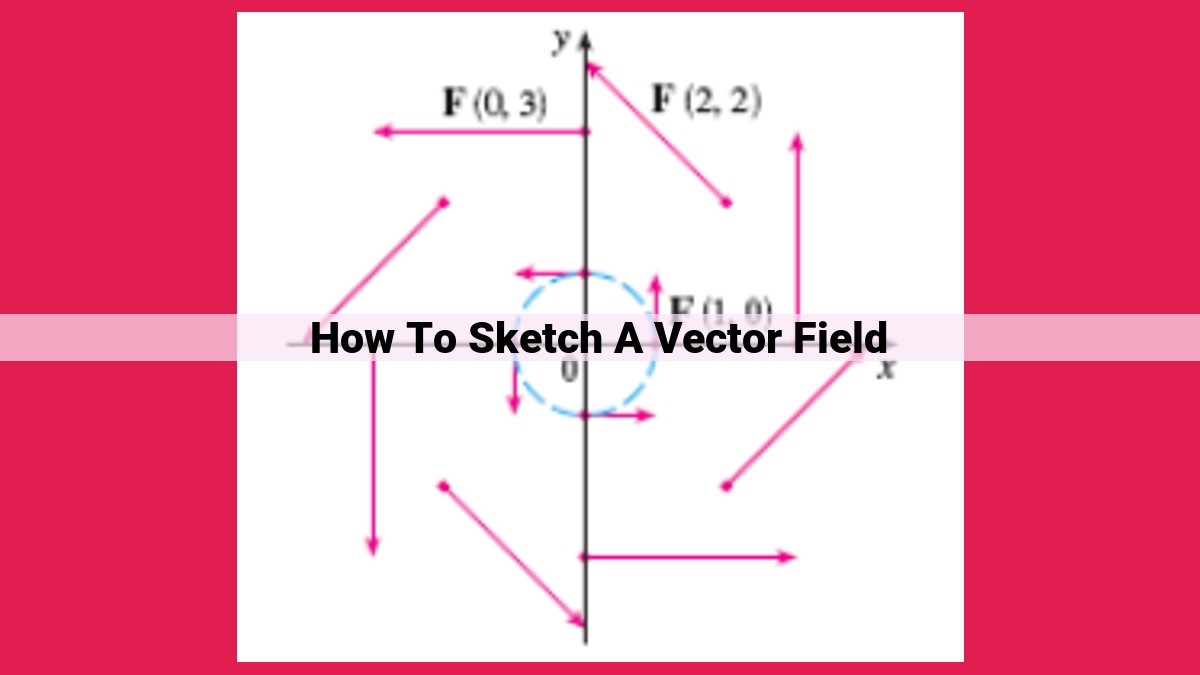
To sketch a vector field, begin by understanding the direction, which indicates the angle of the vector with a reference axis. The magnitude represents the strength or intensity of the quantity. Density indicates the spacing of vectors. Place vectors where the quantity is acting. Scale vectors for easier visualization. Flow lines are curves showing the path of particles moving through the field.

Vector Fields: Unlocking the Secrets of Direction and Magnitude

Step into the fascinating world of vector fields, where quantities are not just numbers but possess both direction and magnitude. These invisible forces shape our surroundings, from the flow of fluids to the movement of celestial bodies. Understanding vector fields empowers us to decipher the hidden patterns and dynamics of our physical world.

What are Vector Fields?

Imagine yourself standing at a busy intersection, surrounded by a swirling vortex of traffic. Each car has its own speed and direction, represented by an arrow. Together, these arrows form a vector field that maps the direction and speed of traffic at every point of the intersection.

Direction: The Pointer’s Guide

The direction of a vector is indicated by its angle with a reference axis. In our traffic intersection example, it’s the alignment of the car with the roads. Vectors can point in any spatial direction, allowing us to represent movements like velocity in two or three dimensions.

Magnitude: Strength Unveiled

In the traffic analogy, the magnitude of a vector corresponds to the speed of the car. It measures the intensity or strength of the quantity being represented. In physics, magnitude is expressed in units like meters per second for velocity and newtons for force.

The Dance of Density

Density in vector fields refers to the spacing between vectors. A dense field indicates a higher concentration of the quantity being represented. Think of a swarm of bees, where each bee represents a vector. A denser swarm indicates a higher concentration of bees in a particular area.

Placement: A Map of Actions

The placement of vectors in a vector field tells us where the quantity is acting. In our traffic intersection, the location of each vector indicates the exact point where a car is moving with a specific speed and direction. This placement allows us to visualize the flow of traffic and identify potential areas of congestion.

Scaling: Making the Invisible Visible

To make vector fields more comprehensible, we often use scaling. This involves adjusting the length of the vectors while maintaining their direction and magnitude. Scaling helps us visualize and compare the relative strengths of different vectors. In the traffic example, longer vectors would represent higher speeds.

Flow Lines: Tracing the Invisible Path

Flow lines are curves that represent the path of particles moving through a vector field. They offer a dynamic representation of how the quantity varies along its trajectory. Think of a river’s current, where each point represents a specific vector and the flow line traces the path of a floating leaf.

Understanding the Direction of Vector Fields

In the realm of physics and mathematics, vector fields play a crucial role in unraveling the intricate patterns of various physical phenomena. They serve as a powerful tool for visualizing the direction and magnitude of quantities that exist in every corner of our universe. In this article, we embark on a captivating journey to explore the fascinating concept of direction in vector fields.

The Compass of Vector Space

At the heart of understanding direction lies the concept of the reference axis. This axis serves as the guiding compass in the realm of vector space, providing a consistent framework for describing the orientation of vectors. The angle formed by a vector with this axis determines its direction.

Navigating the Vector World

In the physical world, countless vector quantities possess a distinct direction. Take, for instance, velocity, a vector that encapsulates both the speed and direction of an object’s motion. Another prime example is force, a vector that embodies the magnitude and direction of an applied force.

Vectors in Action: Velocity and Force

Consider a ball flying through the air. Its velocity vector points in the direction it is moving, providing an immediate grasp of its flight path. Similarly, when you apply a force to an object, the force vector indicates the exact direction in which the force is acting.

In the grand tapestry of nature, countless phenomena are governed by direction. From the flow of water in a river to the electromagnetic forces that shape our universe, understanding direction provides a profound insight into the behavior of the world around us. So, let us continue our exploration of vector fields and uncover the other captivating concepts that lie ahead.

Concept 2: Magnitude

In the realm of vector fields, magnitude is a crucial concept that measures the strength or intensity of the quantity represented by the vector. It’s like a volume knob on a stereo that controls how loud the music plays. Just as a high volume produces a louder sound, a higher magnitude indicates a stronger force, velocity, or other physical quantity.

Imagine a wind blowing across the ocean. The magnitude of the wind vector at a particular location represents the force of the wind pushing against a sailboat’s sail. The higher the magnitude, the stronger the wind and the greater the force applied to the boat.

Another example is the electric field surrounding a charged particle. The magnitude of the electric field at a point away from the particle indicates the strength of the electric force acting on another charged particle placed at that point. The greater the magnitude, the stronger the electric force and the more it affects the other particle.

Understanding the magnitude of a vector field helps us determine the intensity of various physical phenomena. It’s like having a measuring stick that allows us to compare and quantify the strength of different forces, velocities, or other quantities. In essence, the magnitude of a vector provides a numerical value that quantifies the magnitude of the phenomenon it represents.

Concept 3: Density – Unraveling the Spacing of Vectors in a Vector Field

In the realm of vector fields, density emerges as a crucial concept that unveils the distribution of vectors within this vibrant landscape. Think of it as the measure of how tightly packed the vectors are, providing insights into the intensity of the forces they represent.

For instance, in a vector field depicting the concentration of a substance, the density of the vectors indicates the spacing between the molecules or particles. Similarly, in a field representing gravitational field strength, the density of the vectors reflects the closeness of the gravitational forces.

Density thus serves as a bridge between the magnitude of the vectors and their spatial arrangement. It allows us to visualize the strength of a field not only in terms of its individual vectors but also as an overall collective. Imagine a swarm of bees buzzing around a honeycomb, their density revealing not just their individual nectar-collecting abilities but the hive’s overall efficiency.

Understanding vector field density empowers us to decipher the patterns and dynamics of the physical phenomena they represent. It paints a vivid picture of distribution, enabling us to pinpoint areas of high concentration or intensity and visualize the flow and interactions within the field.

Concept 4: Placement

The placement of vectors in a vector field is paramount as it indicates the exact location where the quantity represented by that vector is acting. Imagine a map of wind patterns, where each arrow represents the direction and speed of the wind at a specific point. The placement of these arrows on the map pinpoints the exact location where the wind is blowing in that direction and with that speed.

This concept is closely intertwined with uniformity and the representation of distributions. In a uniform vector field, vectors are equally spaced throughout the field, indicating a consistent quantity across the entire area. Conversely, a non-uniform vector field will have vectors that are unevenly distributed, reflecting variations in the quantity it represents.

For instance, consider a temperature distribution map. The placement of vectors on this map would reveal the exact locations where different temperatures are present. Densely packed vectors indicate high concentrations of a specific temperature, while sparsely placed vectors represent areas with lower concentrations.

By understanding the placement of vectors in a vector field, we not only gain insight into the location of the quantity, but also its distribution pattern. Whether it is a uniform spread or a highly localized concentration, the placement of vectors effectively visualizes the behavior of the quantity across the entire field.

Concept 5: Scaling

• Describe the use of scaling to make vectors easier to visualize and compare.
• Explain how scaling relates to concepts like comparability and visibility.

Concept 5: Scaling

Making vector fields easier to visualize and compare is a key aspect of their analysis. Scaling is a technique that plays a crucial role in this process. Scaling involves adjusting the magnitude of vectors in a field to make them more suitable for visualization and comparison. By scaling, we can ensure that all vectors are within a manageable range of sizes, making them easier to see and compare their relative strengths.

Scaling also relates to concepts like comparability and visibility. When comparing vectors of different magnitudes, scaling allows us to bring them to the same level of visibility. This way, we can easily identify the larger or smaller vectors and make informed comparisons. Moreover, scaling enhances the visibility of vectors, especially when dealing with complex vector fields with vectors of varying sizes. By scaling, we can make the vectors more visually distinct, reducing clutter and improving the overall clarity of the field.

Proper scaling is crucial for effective visualization and comparison of vector fields. It allows us to highlight important details, make comparisons, and draw meaningful conclusions from the data represented by the vectors. Scaling is an essential technique in the analysis of vector fields, ensuring that this complex data is presented in a way that is both informative and visually appealing.

Concept 6: Flow Lines

• Introduce flow lines as curves that represent the path of particles moving through a vector field.
• Discuss related concepts such as streamlines and trajectories.

Concept 6: Flow Lines: Mapping the Motion of Quantities

Vector fields are powerful tools for visualizing the direction and magnitude of physical quantities. One of the most captivating ways to explore these fields is through the concept of flow lines.

The Path of Particles

Imagine a river flowing through a landscape. The water particles dance and move, each following a unique path determined by the contours of the riverbed. Flow lines in a vector field perform a similar dance, tracing the trajectories of particles moving through the field.

Just as the river’s currents determine the direction of water flow, vector fields guide the movement of particles. The direction of flow lines corresponds to the direction of the vectors at each point in the field.

Streamlines and Trajectories

Flow lines are also known as streamlines in fluid dynamics and trajectories in particle physics. These terms all describe the paths that particles take as they move through a vector field. By tracing these flow lines, we can visualize the movement of fluids, particles, or other quantities represented by the vector field.

Unraveling the Mysteries of Vector Fields

Flow lines are invaluable tools for understanding vector fields. They help us:

• Visualize Motion: By tracing flow lines, we can visualize the direction and path of moving particles.
• Identify Patterns: Flow lines can reveal patterns in vector fields, such as eddies, vortices, and convergence zones.
• Understand Complex Phenomena: Flow lines can help us comprehend complex phenomena, such as fluid flow, heat transfer, and particle motion.

Flow lines offer a dynamic and intuitive way to explore the fascinating world of vector fields. By understanding the concept of flow lines, we gain a deeper appreciation for the directional nature of physical quantities and the intricate patterns that they create.