Unlocking Systems Of Equations: Types, Solvability, And Solution Methods

A system of equations consists of two or more equations with the same variables. Consistent systems have at least one solution, while inconsistent systems have no solutions. Solutions to systems can be unique (one solution), infinitely many (all ordered pairs satisfy the system), or no solution (no ordered pair satisfies the system). Consistent systems have consistent solutions, while inconsistent systems have inconsistent solutions. The substitution, elimination, and graphing methods are commonly used to solve systems of equations, each with its advantages and disadvantages.

In the realm of algebra, where numbers dance and equations unravel, we encounter a captivating concept known as a system of equations. A system of equations is a set of equations involving two or more variables. These variables are like enigmatic characters, hiding within the equations, waiting to be uncovered.

A system of equations can be consistent or inconsistent. Consistent systems are those that have at least one solution, where all equations are satisfied simultaneously. Inconsistent systems, on the other hand, have no solutions. They represent situations where the variables cannot fulfill the requirements of all the equations.

Characteristics of Consistent and Inconsistent Systems

Consistent systems typically exhibit one of three scenarios:

• Unique solution: This system has one set of numbers that satisfies all equations.
• Infinitely many solutions: The system has an endless number of solutions, with variables related in a specific way.
• Dependent equations: The equations are not independent; one equation can be derived from the others.

In contrast, inconsistent systems are characterized by:

• No solutions: The equations cannot be satisfied by any set of numbers.
• Contradictions: One equation contradicts the others, making it impossible to find a solution.

Solving Systems of Equations: Unlocking Multiple Solutions

Imagine you’re a detective tasked with solving a mysterious crime. To crack the case, you need to uncover hidden connections and piece together clues from multiple sources. Similarly, in mathematics, solving systems of equations involves finding the missing pieces that link together multiple equations.

The Essence of a Solution

In the world of mathematics, a solution to a system of equations is a set of values that, when plugged into each equation, makes all the equations simultaneously true. It’s like finding the secret combination that unlocks the puzzle box.

Unveiling the Solution Landscape

The solution landscape for systems of equations can vary widely, depending on the nature of the system. Let’s explore the different possibilities:

• Unique Solution: This is the holy grail of equation-solving. When you find a unique solution, it means that there is only one set of values that satisfies all the equations. It’s like finding the missing piece to a jigsaw puzzle.
• Infinitely Many Solutions: Sometimes, multiple sets of values can satisfy a system of equations. In this case, we have an infinite number of solutions, represented by a line or plane that encompasses all the valid combinations. It’s like discovering that there are countless paths leading to the same destination.
• No Solution: Alas, not all puzzles have solutions. When a system of equations is inconsistent, there is no set of values that can simultaneously satisfy all the equations. It’s like trying to force a square peg into a round hole.

Consistent and Inconsistent Systems

In the realm of algebra, systems of equations play a pivotal role in solving real-world problems. Understanding the nature of these systems is crucial for finding solutions that accurately reflect the underlying relationships. When it comes to solving a system of equations, we encounter two distinct possibilities: consistent systems and inconsistent systems.

Consistent Systems

A system of equations is considered consistent if it has at least one solution, meaning there exists a set of values for the variables that satisfy all the equations simultaneously. Consistent systems are further categorized into two types:

• Independent System: A system with one unique solution for the variables.
• Dependent System: A system with infinitely many solutions. In this case, the variables are related linearly, and their values can vary, maintaining a constant relationship.

Inconsistent Systems

On the other hand, an inconsistent system is one that has no solution. This occurs when the equations in the system contradict each other, making it impossible to find a set of values that satisfy all of them.

Identifying Consistent and Inconsistent Systems

To determine whether a system is consistent or inconsistent, we can use various methods:

• Substitution Method: Substitute the solution of one equation into the other to check if the result satisfies both equations.
• Elimination Method: Eliminate one variable by adding the equations multiple times, noting that this preserves consistency.
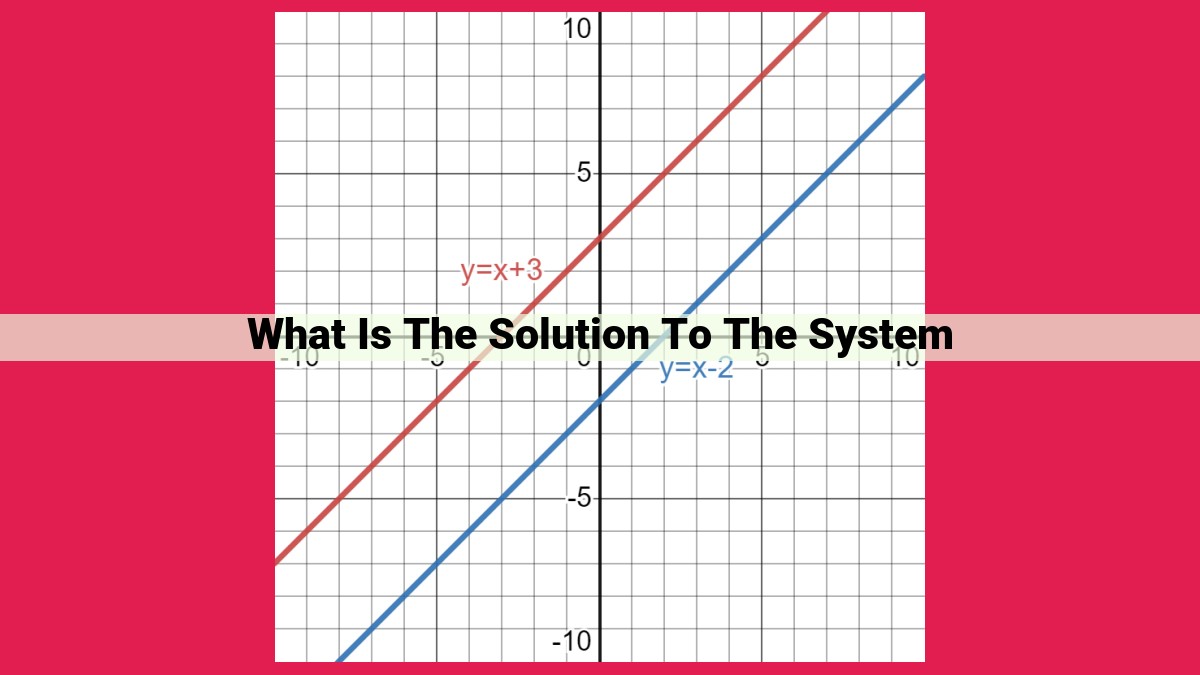
• Graphing Method: Graph both equations on a coordinate plane. A consistent system will have either one point of intersection (unique solution) or infinitely many points of intersection (dependent system). An inconsistent system will have no point of intersection.

Identifying the nature of a system of equations is essential for finding the appropriate solution method. By understanding the properties of consistent and inconsistent systems, we can effectively solve these equations and gain valuable insights into the relationships they represent.

Methods for Solving Systems of Equations

Substitution Method

The substitution method is a straightforward approach that involves solving one equation for one variable and then substituting that expression into the other equation.

Steps:

1. Solve one equation for one variable. Choose the equation that has a variable with the most straightforward coefficient.
2. Substitute the expression for the variable into the other equation. This creates a new equation with only one variable.
3. Solve the new equation. This will give you the value of the remaining variable.
4. Substitute the value of the variable back into the original equation to find the value of the other variable.

Advantages:

• Easy to use
• Suitable for small systems with simple coefficients

Disadvantages:

• Can become messy for large or complex systems
• May lead to fractions or decimals

Elimination Method

The elimination method involves adding or subtracting the equations to eliminate one variable.

Steps:

1. Make the coefficients of one variable the same in both equations. Multiply one or both equations by a number to achieve this.
2. Add or subtract the equations. This will eliminate one variable.
3. Solve the new equation. This will give you the value of the remaining variable.
4. Substitute the value of the variable back into one of the original equations to find the value of the other variable.

Advantages:

• Works well for all types of systems
• Can be used to solve systems with fractions or decimals

Disadvantages:

• Can lead to large coefficients or fractions

Graphing Method

The graphing method is a visual approach that involves graphing both equations on the same coordinate plane.

Steps:

1. Graph each equation on the coordinate plane.
2. The point where the lines intersect is the solution to the system of equations.

Advantages:

• Provides a clear visual representation of the solution
• Useful for systems that are difficult to solve algebraically

Disadvantages:

• Not as precise as algebraic methods
• May not be suitable for all systems (e.g., systems with no solution or infinitely many solutions)