Units Of Slope: Essential Metrics For Inclined Surfaces In Engineering And Beyond

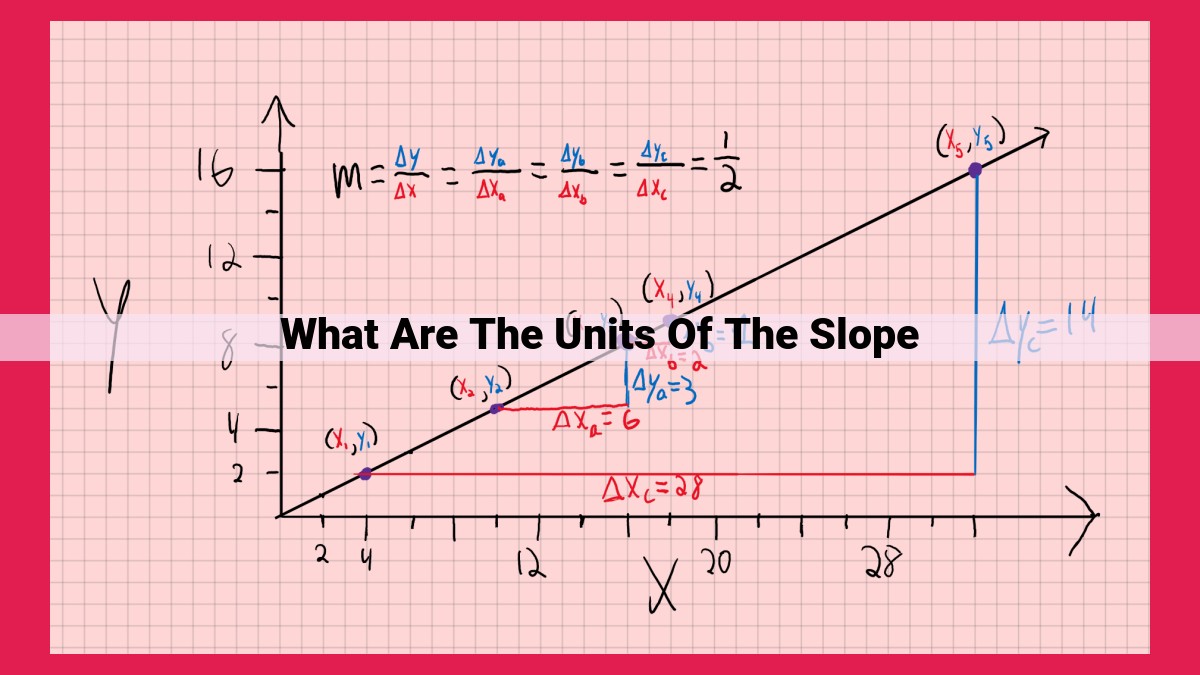
The units of slope, expressing the steepness of a line or surface, vary depending on the context. The basic unit is run over rise, representing the ratio of horizontal distance (run) to vertical distance (rise), resulting in units like meters per meter or feet per foot. Percent slope expresses the slope as a percentage of rise over run, while degrees measure the angle of inclination with respect to the horizontal, using trigonometric functions for conversion between units. Understanding these units is crucial in engineering, construction, geography, and everyday situations involving inclined surfaces.

• Definition and significance of slope
• Overview of related concepts such as rise, run, and gradient

Understanding Slope: A Beginner’s Guide to Inclination

In the world around us, slope plays a crucial role, describing the steepness or inclination of surfaces. From the gentle slopes of rolling hills to the towering mountains that reach towards the heavens, slope is an integral part of our landscape and has a wide range of applications in engineering, science, and everyday life.

Defining Slope

Slope is a measure of the vertical change in elevation over the horizontal distance along a line. It is expressed as the ratio of rise (the vertical change) to run (the horizontal change). The rise is the difference in height between two points, while the run is the distance between these points along the horizontal axis.

Related Concepts: Rise, Run, and Gradient

To understand slope, it’s important to familiarize yourself with related concepts like rise, run, and gradient. Rise measures the vertical distance covered, run measures the horizontal distance covered, and gradient is another term for slope. These terms are often used interchangeably, but slope specifically refers to the numerical value that describes the steepness of a line.

Calculating Slope

Calculating slope is straightforward using the formula:

Slope = Rise / Run

For example, if a line rises 5 units vertically and runs 10 units horizontally, its slope would be 5/10, which simplifies to 1/2. This means that for every 2 units of horizontal distance, the line rises 1 unit vertically.

Applications of Slope

Slope has numerous applications in various fields, including:

• Engineering and Construction: Determining the steepness of roads, bridges, and other structures to ensure safety and stability.
• Science: Modeling geometric relationships, calculating forces on inclined surfaces, and analyzing motion along slopes.
• Everyday Life: Assessing the steepness of hills or roofs, planning walking or cycling routes, and understanding geographical features.

Slope is a fundamental concept that describes the inclination or steepness of surfaces. It is calculated as the ratio of rise to run and has a wide range of applications across multiple disciplines. Understanding slope is essential for anyone interested in engineering, science, or simply navigating the world around them.

Calculating Slope: Unveiling the Rise Over Run Formula

In the realm of mathematics and geometry, the concept of slope plays a crucial role in describing the steepness or gradient of a line. When traversing a slope, we encounter two key components: the rise and the run. The rise represents the vertical change, while the run signifies the horizontal change. To determine the slope of a line, we employ a fundamental formula: rise over run.

Imagine yourself navigating a mountain trail, ascending and descending its rugged slopes. As you climb, you gain altitude, which represents the rise. The distance you cover along the trail, on the other hand, is the run. The slope of the trail, therefore, is calculated by dividing the rise by the run, giving you a numerical value that quantifies the trail’s steepness.

To visualize this concept, consider the slope triangle, a right-angled triangle formed by the rise, run, and the hypotenuse. The angle opposite the rise is known as the angle of inclination. By measuring the rise and run, or by determining the angle of inclination, we can calculate the slope using trigonometric functions.

The slope triangle provides a geometric representation of the rise over run formula. It illustrates how the slope can be determined from the dimensions of the triangle, making it a valuable tool for understanding and calculating slope in various applications.

Units of Slope: Unraveling the Significance

In describing the inclination of surfaces, expressing their slope accurately is paramount. Slope, defined as the ratio of vertical height (rise) to horizontal distance (run), can be expressed in various units, each with its own advantages and applications.

Run over Rise: A Builder’s Measure

In engineering and construction, the most common unit for slope is the run over rise. This ratio, often denoted as a fraction, or “X:Y” format, represents the number of horizontal units covered for every vertical unit ascended. For instance, a slope of “1:5” indicates that for every unit of vertical rise, five units of horizontal distance are covered. This unit is particularly useful for determining the feasibility of structures, such as ramps and stairs, ensuring the slope is accessible and compliant with building codes.

Percent Slope: Expressing Steepness Conveniently

Many prefer to express slope as a percent, calculating it as the rise divided by the run, multiplied by 100. For example, a slope of 1:10 would equate to a 10% slope. The simplicity of this unit makes it highly effective for describing the steepness of slopes, especially in contexts where precise measurements are not required, such as when discussing the grade of roads or hills.

Degrees: A Geographic and Navigational Tool

In geography and navigation, degrees are often used to measure slope. Calculated as the angle formed between the slope and the horizontal plane, degrees provide a direct indication of the steepness. Slopes with steeper angles have a higher degree value, while those with gentler slopes have a lower value. This unit is particularly useful in cartography, where contour lines on maps depict areas of equal slope using degree values.

Knowing the appropriate units for slope is crucial for effective communication and accuracy in various fields. Understanding their unique advantages empowers you to choose the unit that best suits your needs, ensuring clarity and precision in describing the inclination of surfaces, from the slopes of roads to the contours of mountains.

Other Related Concepts

• Distance: path length along the slope
• Angle of Inclination: slope steepness measure

Other Related Concepts

Beyond slope, two other essential concepts come into play: distance and angle of inclination.

Distance refers to the path length traveled along the slope, typically measured in units of meters, feet, or miles. This represents the actual length of the sloping surface you’re dealing with.

Angle of inclination, on the other hand, quantifies the steepness of the slope. It’s the angle formed between the slope and a horizontal line, typically expressed in degrees. This measurement helps us visualize and compare the steepness of different slopes.

Conversion Between Slope Units: Simplifying Slopes

In the world of slopes, navigating between different units can be a slippery slope. But with the right trigonometric tools, we can convert between run-over-rise, percent slope, and degrees effortlessly.

Unveiling the Secrets of Trigonometric Conversion

The key to unlocking the conversion code lies in understanding the geometric relationship between these slope units. We can visualize the slope as a triangle, where the rise (vertical change) is adjacent to the run (horizontal change), forming an angle known as the angle of inclination.

Armed with this knowledge, we can use trigonometric functions to establish the following conversion equations:

• Percent slope to degrees: percent slope = tan(angle of inclination) x 100
• Degrees to percent slope: angle of inclination = arctan(percent slope/100)
• Run-over-rise to degrees: angle of inclination = arctan(rise/run)
• Degrees to run-over-rise: rise/run = tan(angle of inclination)

With these equations in hand, converting between units becomes a breeze. By substituting values and applying the appropriate trigonometric function, we can determine the desired slope unit with ease.

Applications of Slope: Beyond Mathematics

Slope, a fundamental concept in geometry, extends its reach far beyond academic calculations. In everyday life, from the roads we drive on to the roofs over our heads, slope plays a crucial role in engineering, science, and our physical environment.

Determining Steepness

The steepness of a surface is directly related to its slope. Road engineers carefully consider slope when designing highways to ensure safe and efficient travel. Hillside communities must contend with varying slopes, determining the appropriate level of incline for roads and structures. Even the angle of your roof affects factors such as water drainage and snow accumulation.

Calculating Forces and Torque

When an object rests on an inclined surface, gravity exerts a force parallel to the slope. The slope determines the magnitude of this tangential force. Engineers factor slope into designs of conveyors, inclined planes, and ramps to calculate the force required for movement. Similarly, the slope of a surface influences the torque required to rotate objects, such as screws, nuts, and pulleys.

Modeling Geometric Relationships

Slope can be used to model geometric relationships and solve complex problems. In architecture, the slope of a roof truss determines the distribution of weight and stress. In physics, scientists use slope to represent the linear equations of motion. By understanding the slope of a line, engineers, designers, and researchers can predict behavior, analyze data, and make informed decisions.

In the realm of everyday life, slope has a tangible impact on our interactions with the built environment. From determining the ease of rolling a lawn to choosing a suitable bike path, the slope of surfaces shapes our experiences and influences our choices.