Understanding The Vertex Of An Absolute Value Function: A Comprehensive Guide
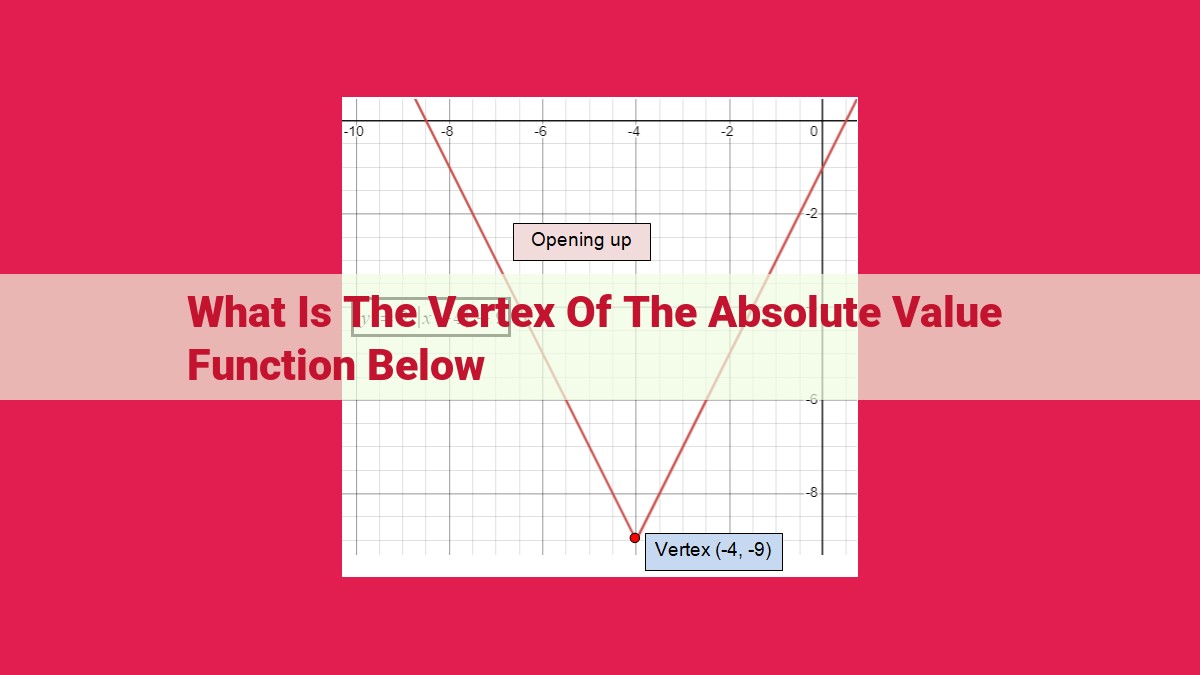
The vertex of an absolute value function f(x) = |x – h| + k is the point (h, k) where the graph changes direction and the parabola is symmetrical. It is the lowest point if h > 0, indicating a minimum value of f(h) = k, or the highest point if h < 0, representing a maximum value of f(h) = k. The vertex divides the parabola into two parts, where f(x) = x – h for x ≥ h and f(x) = -x + h for x < h.
Understanding the Vertex of an Absolute Value Function
In the realm of mathematics, functions play a pivotal role in describing the relationship between variables. One such function, the absolute value function, exhibits a unique characteristic known as its vertex. To delve into the significance of this vertex, we must first establish a clear understanding of the absolute value function and the fundamental concept of the vertex of a parabola.
The Absolute Value Function
The absolute value function, denoted by |x|, transforms any real number x into its non-negative equivalent. This function is defined as:
|x| = x if x ≥ 0
|x| = -x if x < 0
Graphically, the absolute value function resembles a V-shaped curve. The graph consists of two linear segments that meet at a point called the vertex.
The Vertex of a Parabola
In the context of parabolas, the vertex represents the point where the parabola changes direction. It serves as the axis of symmetry, which is a vertical line that divides the parabola into two congruent halves. The y-intercept of the parabola, where it intersects the y-axis, provides additional insight into the function’s behavior.
The Vertex of an Absolute Value Function
The vertex of an absolute value function assumes special importance. It reveals whether the function exhibits a minimum or a maximum value.
- Minimum Value: If
his positive (h > 0), the vertex is a point of minimum value. In this case, the function has a minimum value off(h) = k. - Maximum Value: If
his negative (h < 0), the vertex is a point of maximum value. The function then has a maximum value off(h) = k.
Furthermore, the vertex plays a crucial role in determining the range of the function. The range represents the set of all possible output values that the function can produce. For an absolute value function, the range is determined by the vertex: it is the set of all values greater than or equal to |k|.
The vertex of an absolute value function provides invaluable insights into the behavior of the function. By understanding its properties and significance, we can effectively analyze and interpret the function’s characteristics. Whether it represents a minimum or maximum value, the vertex serves as a critical point of reference for comprehending the function’s overall behavior.
Unveiling the Vertex of an Absolute Value Function
In the realm of mathematics, absolute value functions are a cornerstone of various mathematical concepts. They possess a unique characteristic known as the vertex, which plays a pivotal role in understanding their behavior and properties.
The equation for an absolute value function is given by:
f(x) = |x - h| + k
where h represents the horizontal shift and k represents the vertical shift. Graphically, absolute value functions exhibit a distinctive V-shape, with the vertex at the point (h, k).
To comprehend the nature of this vertex, we delve into the function’s piecewise definition:
f(x) = x - h if x ≥ h
f(x) = -x + h if x < h
This definition illustrates that the function behaves differently for values greater than or less than h, the value of the horizontal shift.
The vertex of an absolute value function marks the point where the function changes direction. It lies on the axis of symmetry, which is a vertical line passing through the vertex. The vertex also corresponds to the y-intercept of the function, where it intersects the y-axis.
The vertex’s location determines whether the function has a minimum or maximum value. If h is positive, the vertex is a minimum point, indicating the lowest value the function can attain. Conversely, if h is negative, the vertex is a maximum point, signifying the highest value the function can reach.
Understanding the vertex of an absolute value function is vital for analyzing its behavior. It provides insights into the function’s range, symmetry, and overall shape. Through its unique properties, the vertex serves as a cornerstone in comprehending the intricate nature of absolute value functions.
Unveiling the Vertex of an Absolute Value Function: A Guide to Its Significance
In the realm of mathematical functions, the absolute value function stands out with its distinctive V-shaped graph. At the heart of this intriguing curve lies a pivotal point known as the vertex. It is here that the parabola abruptly changes direction, giving rise to a treasure trove of insights into the function’s behavior.
The vertex, the point where the parabola reverses course, marks the axis of symmetry, an imaginary vertical line that bisects the parabola into two perfectly mirrored halves. It is at the vertex that we encounter the y-intercept, the point where the parabola intersects the y-axis, representing the function’s starting value.
These three elements—vertex, axis of symmetry, and y-intercept—form the fundamental scaffolding of an absolute value function. They provide a roadmap for understanding the function’s shape, its range, and its overall characteristics.
The vertex’s unique position also determines whether the function has a minimum or maximum value. If the value of h in the function’s equation, f(x) = |x – h| + k, is positive, the vertex represents a minimum point. In this scenario, the function’s lowest point is located at the y-coordinate of the vertex, f(h) = k.
Conversely, if h is negative, the vertex becomes a maximum point. Here, the function reaches its highest point at f(h) = k. This delicate balance between h and the vertex’s nature underscores the profound impact the vertex has on the function’s behavior.
In summary, the vertex of an absolute value function is a nodal point that encapsulates the function’s key characteristics. It reveals the function’s axis of symmetry, its y-intercept, and whether the function exhibits a minimum or maximum value. Understanding the vertex is akin to unlocking the secrets of the absolute value function, enabling us to decipher its shape, range, and behavior with effortless grace.
Understanding the Vertex of an Absolute Value Function
When exploring absolute value functions, the concept of the vertex holds immense significance. The vertex serves as the turning point of the function’s parabolic shape, influencing its behavior and determining its key characteristics.
Vertex: The Turning Point
Imagine a V-shaped graph, a staple feature of absolute value functions. The vertex is the pivotal point where the parabola changes direction, transitioning from an upward to a downward curve or vice versa. In this regard, the vertex signifies the point of minimum or maximum for the function.
Minimum or Maximum Value
The nature of the vertex, whether it indicates a minimum or maximum value, hinges on the value of h. When h is positive, the vertex marks the minimum point of the function. This implies that the function assumes its smallest value at this point, which is given by f(h) = k.
Conversely, when h is negative, the vertex transforms into the function’s maximum point. At this juncture, the function reaches its highest value, denoted by f(h) = k.
Range: The Function’s Bounds
The vertex plays a crucial role in defining the range of the absolute value function. The range encompasses the entire set of values that the function can assume. In the case of an absolute value function, the range is bounded below by its minimum value or above by its maximum value. Therefore, understanding the vertex becomes essential to ascertain the range of the function.
In essence, the vertex of an absolute value function stands as a critical point that governs the function’s behavior. Its identification enables us to decipher the function’s minimum or maximum value and subsequently determine the range of values it can attain.