Understanding Slope: A Guide To Data Analysis And Interpretation
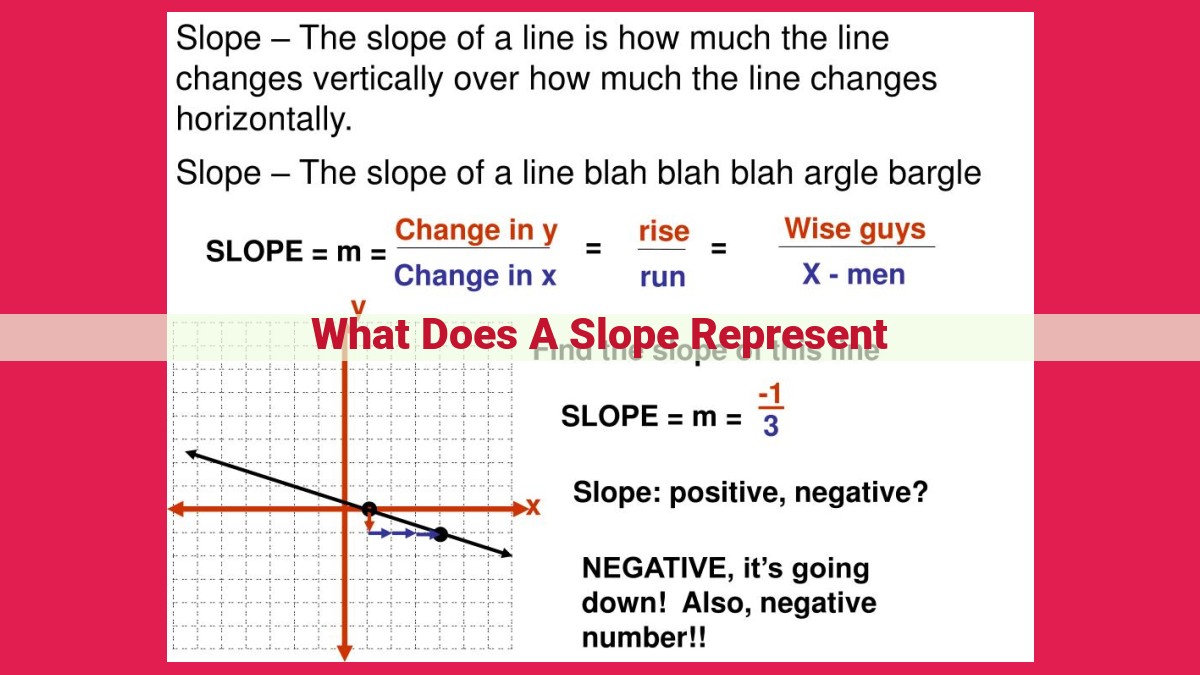
What Does a Slope Represent?
The slope measures the steepness of a line or curve, indicating the rate of change or how quickly a variable changes. It is the ratio of vertical change (rise) to horizontal change (run) of the line. Slope represents the gradient, inclination, or angle between the line and the horizontal axis, and is essential in understanding relationships between variables, predicting outcomes, and analyzing graphs in various fields such as economics, physics, and engineering.
What Does a Slope Represent?
A Glimpse of Steepness
Imagine a treacherous mountain path winding its way upwards, its incline testing the limits of your endurance. The slope of this path, a measure of its steepness, quantifies the arduous journey ahead. Likewise, in the realm of mathematics, slope plays a pivotal role in describing the behavior of lines and curves.
Unveiling the Slope
Simply put, slope measures the rate of change in a line or curve. It represents the ratio of vertical change (or rise) to horizontal change (or run). Consider a straight line on a graph. The slope of this line tells us how much the line rises or falls for every unit of horizontal distance traveled.
In essence, slope serves as a numerical descriptor of steepness. A positive slope indicates a line that slopes upwards, while a negative slope signifies a downward-sloping line. The greater the absolute value of the slope, the steeper the line.
What Does a Slope Represent?
Imagine yourself standing on the side of a hill, looking up at its incline. That incline is what we call a slope, and it provides us with a numerical measure of how steep the hill is.
To calculate the slope, we need to know two things: the vertical change and the horizontal change. The vertical change is how much the hill rises over a certain distance, and the horizontal change is how far the hill stretches out horizontally. The slope is then calculated as the ratio of the vertical change to the horizontal change, expressed as rise over run.
For example, if the hill rises 100 meters over a distance of 200 meters, its slope would be 100/200, which simplifies to 0.5. This tells us that the hill rises 0.5 meters for every meter it stretches out horizontally.
The concept of slope is closely related to several other terms:
- Rate of Change: The slope of a line or curve describes how quickly a variable changes over time or distance.
- Steepness: The greater the slope, the steeper the line or curve appears.
- Gradient: Another term for slope, calculated as the ratio of vertical to horizontal change.
- Inclination: The angle between the line and the horizontal axis.
- Rise Over Run: The ratio of vertical to horizontal change, used interchangeably with slope.
- Tangent of Angle of Elevation: The ratio of vertical to horizontal change, also related to slope.
Rate of Change: How quickly a variable changes over time.
What Does a Slope Represent?
Understanding the Concept of Slope
In mathematics, a slope is a fundamental concept that describes the inclination or steepness of a line or curve. It measures the rate of change in the vertical direction relative to the horizontal direction.
Unveiling the Essence of Rate of Change
Imagine driving your car up a hill. The rate of change in elevation, measured by the slope of the road, determines how quickly you gain altitude. A steep slope indicates a rapid increase in elevation, while a gentler slope signifies a more gradual ascent.
Slope is crucial in understanding the behavior of variables over time. It provides insights into the direction and magnitude of change. A positive slope indicates an increase with time, while a negative slope suggests a decrease. The steeper the slope, the more dramatic the change.
Related Concepts that Illuminate Slope
The concept of slope is intertwined with several related terms:
- Steepness: A measure of the inclination of a slope, expressed as an angle between the line and the horizontal axis.
- Gradient: Synonymous with slope, it represents the ratio between vertical and horizontal changes.
- Rise Over Run: Another expression for slope, referring to the fraction of vertical rise to horizontal distance.
- Tangent of Angle of Elevation: In the context of trigonometry, the ratio of vertical change to horizontal change determines the tangent of the elevation angle.
What Does a Slope Represent?
Understanding the Concept of Slope
Slope, in mathematical terms, signifies the steepness or inclination of a line or curve. It serves as a crucial measure of how vertically a variable changes in relation to its horizontal movements. The concept of slope finds widespread applications in various fields, including engineering, economics, and physics.
Unveiling the Interconnected Terms
Closely associated with slope are a plethora of terms that shed light on its multifaceted nature:
-
Rate of Change: This encapsulates the velocity at which a variable transforms over time. Slope serves as a direct reflection of this rate of change.
-
Gradient: This term is synonymous with slope, denoting the extent of vertical change relative to horizontal change.
-
Inclination: This property measures the angle formed between a line and the horizontal axis, effectively conveying the degree of slope.
-
Rise Over Run: Another expression for slope, it signifies the ratio of vertical change to horizontal change.
-
Tangent of Angle of Elevation: This advanced concept expresses slope as the ratio of vertical change to horizontal change, pertaining specifically to the angle of elevation of a line.
Steepness: A Tale of Angles
Steepness, a cornerstone of slope’s essence, gauges the inclination of a line or curve. It conveys the extent of vertical change over a given horizontal distance. A steeper slope corresponds to a larger angle of inclination, indicating a more rapid rate of vertical change. Conversely, a gentler slope translates to a smaller angle of inclination, suggesting a more gradual rate of vertical change.
In practical applications, understanding steepness is paramount. For instance, in civil engineering, the steepness of a road influences the safety and efficiency of travel. Similarly, in economics, the steepness of a demand curve dictates the responsiveness of consumers to price changes. By grasping the intricate relationship between slope and steepness, we gain valuable insights into the intricacies of our world.
What Does a Slope Represent: A Visual Journey
In our daily lives, we encounter countless lines and curves that describe everything from the trajectory of a thrown object to the shape of a roller coaster. Understanding the steepness of these lines and curves is crucial for making sense of the world around us. Enter slope, the mathematical tool that measures this steepness.
Slope: The Measure of Steepness
Slope, in essence, quantifies how rapidly a line ascends or descends. It is calculated as the ratio of vertical change (rise) to horizontal change (run). For instance, a line that rises 2 units for every 3 units it moves horizontally has a slope of 2/3.
Related Concepts: A Dizzying Gradient
Slope is intertwined with several related concepts:
- Rate of Change: Slope measures the rate at which a variable changes over time or distance.
- Steepness: Slope directly corresponds to steepness, with a larger slope indicating a steeper line.
- Gradient: This term is synonymous with slope and is also calculated as the ratio of vertical to horizontal change.
- Inclination: Inclination describes the angle between a line and the horizontal axis, which is closely related to slope.
Rise Over Run: A Familiar Notion
The concept of slope can be easily understood through the phrase “rise over run.” This simply means the ratio of the vertical distance (rise) to the horizontal distance (run) covered by a line or curve.
Tangent of Angle of Elevation: A Trigonometric Perspective
Another way to conceptualize slope is through trigonometry. The slope of a line is equal to the tangent of the angle of elevation, which is the angle formed between the line and the horizontal axis.
In conclusion, slope is a versatile mathematical tool that provides insights into the steepness and behavior of lines and curves. By understanding slope, we gain a deeper appreciation of the world’s intricate patterns and dynamics.
What Does a Slope Represent?
Definition of Slope
A slope is a mathematical concept that quantifies the steepness of a line or curve. It represents the rate of change or how quickly a variable changes relative to another. More specifically, it is defined as the ratio of vertical change (also known as “rise”) to horizontal change (also known as “run”).
Related Concepts to Slope
-
Steepness: This is a qualitative term used to describe how inclined or steep a slope is. A steep slope has a higher ratio of vertical change to horizontal change, while a less steep slope has a lower ratio.
-
Gradient: This is another term for slope, calculated as the ratio of vertical to horizontal change, just like slope.
-
Inclination: This is the angle between a line and the horizontal axis. It is related to slope in that a greater slope corresponds to a larger inclination.
What Does a Slope Represent?
In the realm of mathematics, a slope wields the power to unravel the secrets of lines and curves, revealing their hidden characteristics. It’s like the key that unlocks the door to understanding their steepness and rate of change. Imagine a line dancing across a graph, its path defined by its unique slope.
Rise Over Run: The Building Blocks of Slope
At the heart of slope lies the concept of rise over run. It’s a simple yet profound ratio that captures the essence of a line’s inclination. Rise represents the vertical change, the distance the line travels up or down. Run, on the other hand, embodies the horizontal change, the distance it moves left or right. When these two values dance together, they form the slope, a measure of the line’s steepness.
Think of a mountain trail winding its way up a hillside. The slope of the trail tells you how steep it is, how much effort it will take to climb. A steeper trail has a larger slope, meaning it rises more sharply for each step you take. Conversely, a gentler trail has a smaller slope, indicating a more leisurely ascent.
In mathematics, slope serves as the universal language for describing the steepness of lines and curves. It’s a powerful tool that unlocks a wealth of information about the behavior of these enigmatic shapes. So, the next time you encounter a line or curve, remember the power of slope. It’s the key to unlocking its hidden mysteries.
What Does a Slope Represent?
Definition of Slope
Imagine you’re hiking up a mountain. The steepness of the trail, that’s slope. Mathematically, slope is the ratio of your vertical climb (how much you go up) to your horizontal distance (how far you walk along the trail).
Related Concepts to Slope
Slope has other cool names:
- Rate of Change: How fast things change over time.
- Steepness: How inclined a line is.
- Gradient: Another word for slope.
- Inclination: The angle between a line and the horizontal.
- Rise Over Run: The ratio of vertical to horizontal change.
One fascinating concept is the Tangent of the Angle of Elevation. It’s the ratio of the vertical height of an object (like that mountain you’re climbing) to its horizontal distance from you. This ratio gives you a precise measurement of how steep the object appears to be.
Slope and Everyday Life
Slope is everywhere! It helps us understand:
- Roof pitch: How steep your roof is influences drainage and energy efficiency.
- Road grades: The slope of a road affects vehicle speed and safety.
- Water flow: Slope determines the direction and speed of water, shaping rivers and landscapes.
- Stock market trends: The slope of a stock’s price line indicates whether it’s rising or falling.
- Heart rate: The slope of the line on a heart rate monitor shows how quickly your heart is beating.
Understanding slope is a valuable tool for navigating our world, from hiking trails to financial markets. By grasping this concept, you can better appreciate the complexity of the world around you.
Ratio of Vertical Change to Horizontal Change: Another term for slope.
What Does a Slope Represent?
In the vast tapestry of mathematics, slopes play a pivotal role in unraveling the mysteries of graphs and the world around us. They measure the steepness of lines and curves, providing insights into rates of change and the relationships between variables.
Understanding Slope: Rise Over Run
At its core, a slope is a measure of how quickly a quantity changes in relation to another. In the case of a line, it represents the ratio of the vertical change (the difference in y-coordinates) to the horizontal change (the difference in x-coordinates). This ratio is commonly referred to as rise over run or vertical change to horizontal change.
In the context of a hilly road, for instance, the slope would indicate how steeply the road ascends or descends. A steep slope, characterized by a large rise over run, would result in a more challenging climb, while a gentle slope, with a smaller rise over run, would be easier to traverse.
Related Concepts to Slope
The concept of slope is intricately intertwined with several other mathematical terms:
- Rate of Change: The rate at which a variable changes over time.
- Steepness: A measure of how inclined a slope is.
- Gradient: Synonymous with slope, expressing the ratio of vertical to horizontal change.
- Inclination: The angle between a line and the horizontal axis.
- Tangent of Angle of Elevation: Another term for slope, calculated as the ratio of vertical to horizontal change.
Applications of Slope
Slopes have far-reaching applications in various fields, including:
- Analyzing the movement of objects in physics
- Determining the efficiency of machines in engineering
- Forecasting financial trends in economics
- Predicting weather patterns in meteorology
By understanding the concept of slope, we gain a deeper appreciation for the intricacies of our world and equip ourselves with a powerful tool for problem-solving and analysis.