Understanding Radius: Its Significance In Geometry And Practical Applications
Radius is a crucial aspect of geometry. It defines the distance from the center to any point on a circle’s edge, influencing its size and shape. Related concepts include diameter (twice the radius) and circumference (related by the formula C = 2πr). Understanding radius is essential for architecture, engineering, science, and art. It enables the calculation of distances, design of circular structures, and creation of symmetrical compositions. In real-world applications, knowing the radius helps us analyze object motion in circular paths and design objects with specific dimensions.
Delving into the World of Circles: Understanding Radius
In the realm of geometry, circles hold a prominent place. These enchanting shapes, defined by their closed, curving perimeter, captivate our imagination with their mesmerizing symmetry. At the heart of every circle lies a pivotal element known as the radius, a concept that unlocks a treasure trove of mathematical mysteries.
The radius of a circle is the distance from its center to any point on its circumference. It serves as a lifeline, connecting the circle’s core to its outer boundaries. This fundamental measurement plays a crucial role in unraveling the secrets that lie within circles, enabling us to decode their properties and unravel their geometric tapestry.
The importance of the radius in geometry cannot be overstated. It forms the basis for calculating other essential circle characteristics, such as diameter and circumference. The diameter, spanning the circle’s widest point, is simply twice the radius. Likewise, the circumference, the distance around the circle’s edge, is elegantly expressed as a multiple of the radius. These relationships underscore the radius’s significance in characterizing circles and unraveling their geometric puzzles.
Concepts Related to Circles:
In the realm of geometry, circles hold a special significance, with their defining feature being their radius. This fundamental concept helps unravel the secrets of these captivating shapes and unlocks a world of mathematical relationships.
Diameter: The Double of Radius
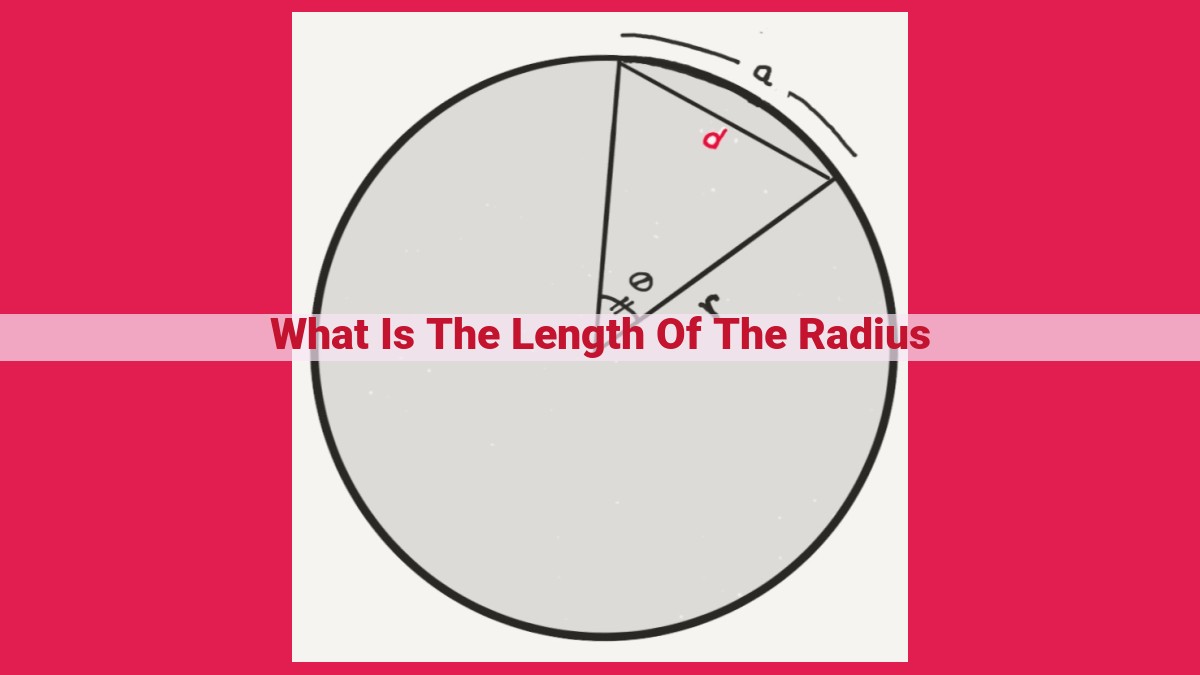
Imagine a line segment that passes through the center of a circle and connects two points on its circumference. This is the diameter, and it bears a special kinship with the radius. The diameter, denoted by d, is always twice the length of the radius, r. In other words, d = 2r.
Circumference: The Circle’s Perimeter
Another key concept linked to radius is the circumference, the distance around the circle’s perimeter. This measurement is expressed using the mathematical constant π (pi), approximately equal to 3.14. The circumference, C, has a profound connection with the radius: C = 2πr. This formula reveals that the circumference is directly proportional to the radius, meaning that as the radius increases, the circumference also increases, and vice versa.
Calculating the Elusive Radius: Unlocking the Secrets of Circles
In the world of geometry, circles reign supreme as symbols of symmetry and harmony. At the heart of every circle lies the enigmatic radius, a length that holds the key to understanding these captivating shapes.
A Formulaic Adventure:
Seeking the radius of a circle is no ordinary quest. It requires the mastery of two powerful formulas that will illuminate the path to this geometric treasure.
- Radius from Circumference:
Like a wizard’s incantation, the formula r = C / 2π emerges, where C represents the circumference, the magical boundary that encircles the circle. Divide the circumference by 2π, the mathematical constant that governs circles, and behold, the radius emerges from the depths of unknown.
- Radius from Diameter:
Another path to the radius awaits through the diameter, a chord that valiantly spans the circle’s heart. The formula r = d / 2 beckons, where d represents the diameter’s grandeur. By halving this majestic length, the radius gracefully reveals itself.
Harnessing the Power of Formulas:
To wield these formulas, envision a circle with a circumference of 30 units. Using the first formula, we embark on a mathematical journey:
- r = C / 2π
- r = 30 / 2π
- r ≈ 4.77 units
Eureka! The radius of this circle is approximately 4.77 units.
Similarly, if we encounter a circle with a diameter of 10 units, the second formula guides us:
- r = d / 2
- r = 10 / 2
- r = 5 units
With precision, we uncover the radius of this circle to be 5 units.
The formulas for calculating radius provide indispensable tools for navigating the world of circles. Whether it’s unraveling the mysteries of architecture, understanding the trajectory of objects in motion, or simply appreciating the beauty of symmetry, the radius remains an essential ally. May these formulas empower you in your geometric explorations, unlocking the secrets of circles that await your discovery.
Practical Applications of Radius: Where Understanding Geometry Empowers Us
In our world brimming with circular forms, the radius, a seemingly simple concept, plays a pivotal role. It’s not just a mathematical abstraction; it’s an indispensable tool in various fields, guiding our creations and understanding the world around us.
Architecture and Engineering
From soaring domes to intricate columns, circular structures abound in architecture. Understanding the radius is paramount for designing these structures, ensuring their strength, stability, and aesthetics. Architects and engineers rely on it to determine the curvature of domes, calculate the load-bearing capacity of columns, and craft aesthetically pleasing circular spaces.
Science and Technology
In the realm of science and technology, radius guides our understanding of motion. When objects move in a circular path, their distance from the center—their radius—determines their speed, acceleration, and trajectory. This knowledge is crucial in fields ranging from celestial mechanics to particle accelerators, helping us understand the complexities of motion.
Art and Design
Circles and their radii have captivated artists for centuries. In painting, photography, and graphic design, the radius dictates the curvature of lines, the symmetry of compositions, and the focal point of the artwork. Understanding this concept empowers artists to create visually engaging and harmonious designs that evoke emotions and convey ideas.
Whether it’s the grand arches of ancient Roman aqueducts, the mesmerizing trajectories of celestial bodies, or the intricate patterns in nature, the radius is a ubiquitous and essential element in our world. Its understanding empowers us to shape our surroundings, unravel the mysteries of the universe, and create beauty. So, the next time you encounter a circle, remember the profound role that its radius plays in our lives.