Understanding The Inverse Relationship Between Period And Frequency: Essential For Physics, Audio, And Music

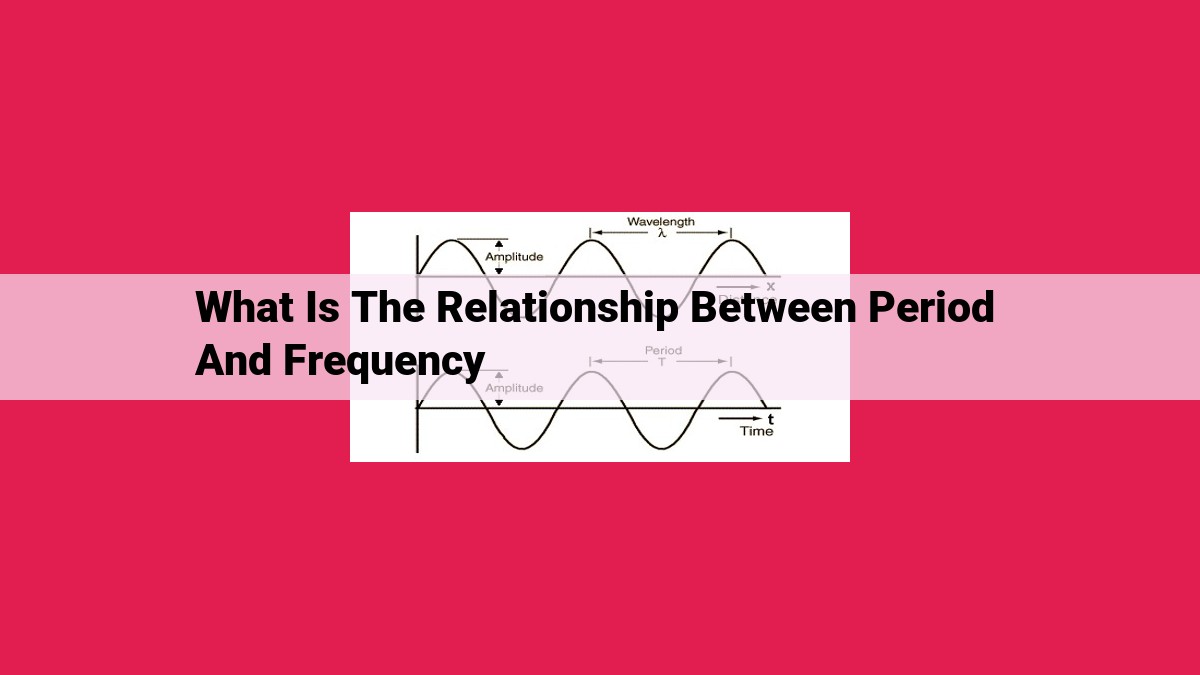
Period, the duration of a complete oscillation, and frequency, the rate of oscillations, have an inverse relationship: as period increases, frequency decreases, and vice versa. This is expressed mathematically as Period = 1 / Frequency. Period and frequency are essential measures in fields like physics, audio engineering, and music, helping quantify the rhythmic behavior of oscillating systems like pendulums, sound waves, and musical notes.

Understanding Period and Frequency: The Rhythm of Oscillations

Imagine yourself swinging on a playground swing, moving rhythmically back and forth. This rhythmic motion is a prime example of oscillation, a repetitive back-and-forth or up-and-down motion that repeats itself over time. To quantify this oscillation, we use two fundamental concepts: period and frequency.

Period measures the duration of one complete oscillation, the time it takes for the swing to move from one extreme point to the other and back again. Frequency, on the other hand, measures the rate of oscillations, or how many times the swing completes a cycle within a given time interval. Understanding period and frequency is crucial in various fields, including physics, engineering, and audio engineering.

Period: The Measure of a Complete Cycle

In the world of oscillations, understanding the concept of period is crucial. Period refers to the time duration required for a complete cycle—a full swing, rotation, or vibration. It’s the temporal measure of an oscillation’s journey from its starting point back to the same point.

Period is closely intertwined with both time and oscillations. Each oscillation, whether it’s the swing of a pendulum or the pulsation of a sound wave, represents a specific time interval. By studying period, we gain insights into the frequency and patterns of these rhythmic movements.

Measuring period involves different units, with seconds being the most common. However, another prevalent unit is Hertz (Hz), which is the inverse of period. One Hertz represents one oscillation per second. By converting period to Hertz, we can conveniently express the frequency of oscillations, or how many times an oscillation occurs within a given time frame.

Frequency: The Pulse of Oscillations

Imagine a rhythmic swing, its arc tracing a graceful path through the air. As the swing moves back and forth, we can count the number of times it completes a full cycle within a given time span. This number, dear reader, is what we call frequency.

Frequency measures the rate at which oscillations occur—the number of cycles completed in a specified time interval. It’s a crucial concept not only in physics but also in fields like engineering, audio, and music.

Every time the swing reaches its highest or lowest point, it completes one oscillation. The more frequent the oscillations, the faster the swing moves. Cycles per second (Hertz) is the common unit for expressing frequency.

In the realm of sound, frequency determines the pitch of musical notes. High-frequency sounds, measured in kilohertz (kHz), are perceived as higher-pitched, while low-frequency sounds, measured in hertz (Hz), are perceived as lower-pitched.

The Inverse Relationship: A Balancing Act

In the realm of oscillations, period and frequency dance in an intricate tango, mirroring each other’s movements in an inverse rhythm. As one expands, the other gracefully contracts, creating a harmonious balance. Let’s unravel this captivating relationship and explore how they interplay in the real world.

Visualize a swinging pendulum, its rhythmic arc a testament to the interplay of period and frequency. Period, measured in seconds, represents the time it takes for the pendulum to complete one full swing, from its highest point to its lowest and back again. Frequency, on the other hand, is the number of swings it makes in a specific time interval, measured in Hertz (cycles per second).

As the pendulum swings slower, its period increases. In this graceful ballet, as the arc widens, the time it takes to complete a single swing elongates. Conversely, as the pendulum’s tempo accelerates, its frequency rises. With each swift swing, it completes more cycles within the same time frame.

This inverse relationship extends beyond the pendulum’s rhythmic sway. It governs all oscillations, from the vibrations of sound waves to the electrical currents in a circuit. In physics, a longer period corresponds to a lower frequency, as seen in the rhythmic motion of springs and oscillating objects. In audio and music, the pitch of a note is determined by its frequency; the higher the frequency, the higher the pitch.

Understanding this inverse relationship is crucial for grasping the rhythmic patterns that shape our world. It empowers us to analyze and predict oscillations in various fields, from engineering and signal processing to the captivating rhythms of music.

The Mathematical Connection: Period and Frequency, Unveiled

In the realm of oscillations, the concepts of period and frequency dance in an elegant interplay. Period, measured in units of time, captures the duration of a single, complete oscillation. Imagine a pendulum swinging back and forth, its period being the time it takes to complete one full cycle.

Meanwhile, frequency, measured in Hertz (Hz), embodies the rate at which oscillations occur. It conveys the number of oscillations completed within a specified time interval. Think of a musical note; its frequency determines its pitch, with higher frequencies corresponding to higher-pitched notes.

The formula that connects these two concepts is a testament to their inverse relationship:

Period (T) = 1 / Frequency (f)

This formula highlights the reciprocal nature of period and frequency. As period increases, frequency decreases, and vice versa. It’s like a seesaw; when one goes up, the other goes down.

Calculating period and frequency using this formula is straightforward. To find the period, simply divide 1 by the frequency. Conversely, to determine the frequency, divide 1 by the period.

This mathematical connection is a powerful tool in understanding oscillations and cyclical phenomena. It enables scientists, engineers, and musicians alike to analyze and manipulate periodic events effectively. From the rhythmic beating of a heart to the vibrations of a guitar string, the formula for period and frequency unlocks a deeper comprehension of the world around us.

The Practical Roles of Period and Frequency

Beyond theoretical definitions, period and frequency play crucial roles in diverse fields:

Physics

In physics, period and frequency govern various phenomena:
– The period of a pendulum’s swing determines its rhythm, while the frequency of a sound wave determines its pitch.
– In electronics, frequency measures the oscillation rate of alternating current.
– In signal processing, period and frequency help analyze and manipulate waveforms.

Engineering

Period and frequency are vital in engineering applications:
– Frequency determines the resonance of structures and bridges, ensuring their stability.
– Period is crucial in control systems for maintaining stability and preventing oscillations.

Audio and Music

In audio engineering and music, period and frequency are fundamental:
– The period of a musical note corresponds to its duration, while the frequency determines its pitch.
– Tuning instruments involves adjusting frequency to achieve harmonious intervals.