Understanding The Normal Distribution: Essential For Statistical Analysis And Hypothesis Testing

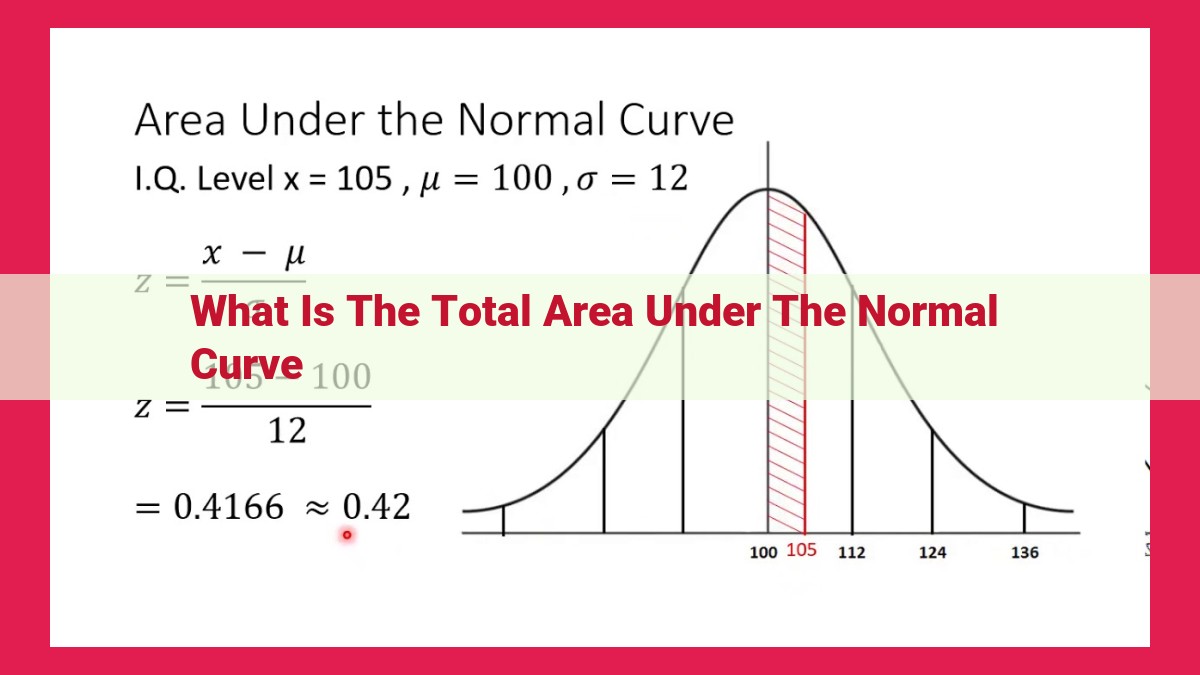
The normal distribution, a bell-shaped curve, is a cornerstone of statistics. The total area under this curve is 1, representing the entire data range. Understanding this area helps determine probabilities of events, make inferences from data, and conduct hypothesis tests. The normal distribution is characterized by its mean, median, mode, standard deviation, and variance, which dictate its spread and shape. Z-scores standardize data, allowing for easy comparisons. Applications span various fields, including probability calculations, sample inferences, and confidence interval determinations. The total area under the normal curve is a crucial concept for comprehending probability and its statistical applications.

The Secrets of the Normal Curve: Unveiling the Total Area

In the realm of statistics, the normal distribution, also known as the Gaussian distribution, reigns supreme. This bell-shaped curve is not just an abstract concept but a fundamental tool that underpins countless statistical analyses. Its importance stems from the fact that it models a wide range of natural phenomena, from heights of individuals to stock market fluctuations.

One crucial aspect of the normal curve is its total area. Understanding this area is like holding the key to unlock the secrets of probability and statistical inference. This blog post embarks on a journey to explore the total area under the normal curve, unraveling its significance and applications.

Understanding Total Area:

• Explain the concept of area under a curve and its significance in the normal distribution.
• Discuss the relationship between the total area and the probability distribution of the normal curve.

Understanding Total Area: The Significance of the Normal Curve

In the realm of statistics, the normal distribution holds a pivotal position. Its bell-shaped curve gracefully depicts a symmetrical distribution, where data points dance around a central mean value. This curve’s underbelly conceals a profound secret: it holds the key to understanding probability in the normal distribution.

The concept of area under a curve is paramount. Imagine this curve as a landscape, with each point on the curve rising above the x-axis like a mountain peak. The area beneath the curve, like a vast valley, represents the likelihood of a data point falling within a particular range.

The total area under the normal curve is always 1, a numerical constant that echoes the total probability of an event occurring. This area is continuous, stretching from -∞ to +∞. As we venture along the curve, the probability gradually shifts from low in the tails to high near the mean.

This integral relationship between area and probability empowers us to predict the likelihood of specific events. By slicing the curve into smaller regions, we can calculate the probability of a data point falling within each fragment. This knowledge unlocks the door to making inferences about our data, whether it’s estimating the probability of a certain outcome or testing hypotheses.

In essence, understanding the total area under the normal curve is akin to deciphering the secret language of probability. It empowers us to unravel the mysteries of data and make informed decisions based on statistical evidence.

Related Concepts: Unveiling the Secrets of the Normal Curve

Beyond the basic understanding of the normal distribution, it’s essential to explore the concepts that play a vital role in unraveling its intricate nature.

Standard Deviation and Variance: Guardians of Data’s Spread

Standard deviation and variance are two inseparable measures that quantify the variability or spread of data points within a normal distribution. Standard deviation represents the average distance of data points from the mean, like a measure of how far the data “deviates” from the center. Variance, on the other hand, is the square of the standard deviation, providing a numerical representation of data’s dispersion.

Mean, Median, and Mode: Statistical Trio for Location

The normal distribution is characterized by three key statistics that pinpoint its central tendencies:

• Mean: The average value of all data points, providing a precise measure of its central location.
• Median: The middle value when data points are arranged in ascending order, representing the point where half the data lies above and half below.
• Mode: The value that occurs most frequently, offering an indication of the most common observation.

In a normal distribution, the mean, median, and mode typically coincide, indicating a symmetrical distribution around the central value.

Probability and Likelihood: The Pillars of Understanding the Normal Curve

Probability and likelihood are fundamental concepts that play a crucial role in comprehending the total area under the normal curve. Probability quantifies the likelihood of an event occurring, expressed as a value between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. Likelihood, on the other hand, refers to the degree of support for a particular hypothesis or event based on available evidence.

The total area under the normal curve represents the probability of all possible outcomes within a given range. By dividing this area into smaller sections, we can determine the probability of an observation falling within specific intervals. For instance, the area to the left of a particular data point corresponds to the probability of observing values less than that point.

Relative frequency is a related concept that describes the proportion of times an event occurs in a large number of independent trials. As the number of trials increases, the relative frequency approaches the theoretical probability of the event. For the normal distribution, the total area under the curve represents the theoretical probability, and the relative frequency of observations within specific intervals converges to this probability as the sample size increases.

By leveraging these concepts, we can use the normal curve to make inferences about the likelihood of events and the distribution of data. This understanding is essential for various statistical applications, including calculating probabilities, drawing conclusions from samples, and testing hypotheses.

Z-Scores: Standardizing Data from the Normal Distribution

In the realm of statistics, the normal distribution reigns supreme. It’s a bell-shaped curve that governs the behavior of countless natural phenomena, from heights and weights to exam scores and financial fluctuations. One fundamental concept in understanding this distribution is the total area under the curve.

Enter the Z-score, a powerful tool for standardizing data from the normal distribution. A Z-score measures how many standard deviations a particular data point is above or below the mean (average) of the distribution. This transformation allows us to compare data from different distributions on a common scale.

But what are standard deviations and percentiles? Standard deviation is a measure of how spread out the data is. A smaller standard deviation indicates data that clusters closely around the mean, while a larger standard deviation indicates more dispersion. Percentile, on the other hand, divides the distribution into equal parts. For example, the 25th percentile (also known as the first quartile) represents the data point at which 25% of the data falls below.

Z-scores are closely related to percentiles. A Z-score of 0 corresponds to the mean, or 50th percentile. A Z-score of 1 corresponds to the data point that is one standard deviation above the mean, which is also the 84th percentile. Conversely, a Z-score of -2 corresponds to the data point that is two standard deviations below the mean, or the 2nd percentile.

Understanding Z-scores empowers us to make inferences about the probability of events. For instance, if a student’s Z-score on a standardized test is 1.5, we know that approximately 93% of the population would score lower than them on that test. This information allows us to quantify the likelihood of outcomes and make informed decisions.

Applications of the Total Area Under the Normal Curve

The total area under the normal curve plays a pivotal role in numerous statistical applications, enabling us to unlock hidden insights from data. These applications span a wide range of disciplines, empowering researchers, analysts, and decision-makers alike.

Calculating Probabilities of Events

One of the most fundamental applications of the normal curve is calculating the probability of events occurring within a given range of values. This is achieved by determining the area under the curve between two specific data points. For instance, suppose we know that the average height of adults follows a normal distribution with a mean of 68 inches and a standard deviation of 2.5 inches. Using the total area under the curve, we can calculate the probability of randomly selecting an adult whose height falls within the range of 65 to 70 inches.

Making Inferences from Sample Data

Statistical inference allows us to make educated guesses about a larger population based on a smaller sample size. The normal distribution provides a framework for making such inferences. By analyzing the distribution of sample data, we can estimate the probability distribution of the population from which the sample was drawn and draw conclusions about its characteristics. This is essential for making decisions based on limited data.

Determining Confidence Intervals

Confidence intervals are ranges of values within which we can be confident that a population parameter, such as the mean or the variance, will fall. Using the total area under the normal curve, we can calculate the probability that a sample statistic will lie within a certain range of values around the true population parameter. This helps us make informed decisions and quantify the uncertainty associated with our estimates.

Hypothesis Testing

Hypothesis testing is a statistical method used to determine whether there is sufficient evidence to reject a null hypothesis, which assumes that there is no significant difference between two populations. The total area under the normal curve is used to determine the probability of obtaining a sample result that is as extreme or more extreme than the one observed, assuming the null hypothesis is true. If this probability is sufficiently low, we reject the null hypothesis and conclude that there is a statistically significant difference between the populations.