Understanding Inertia: How Mass And Density Impact Resistance To Motion

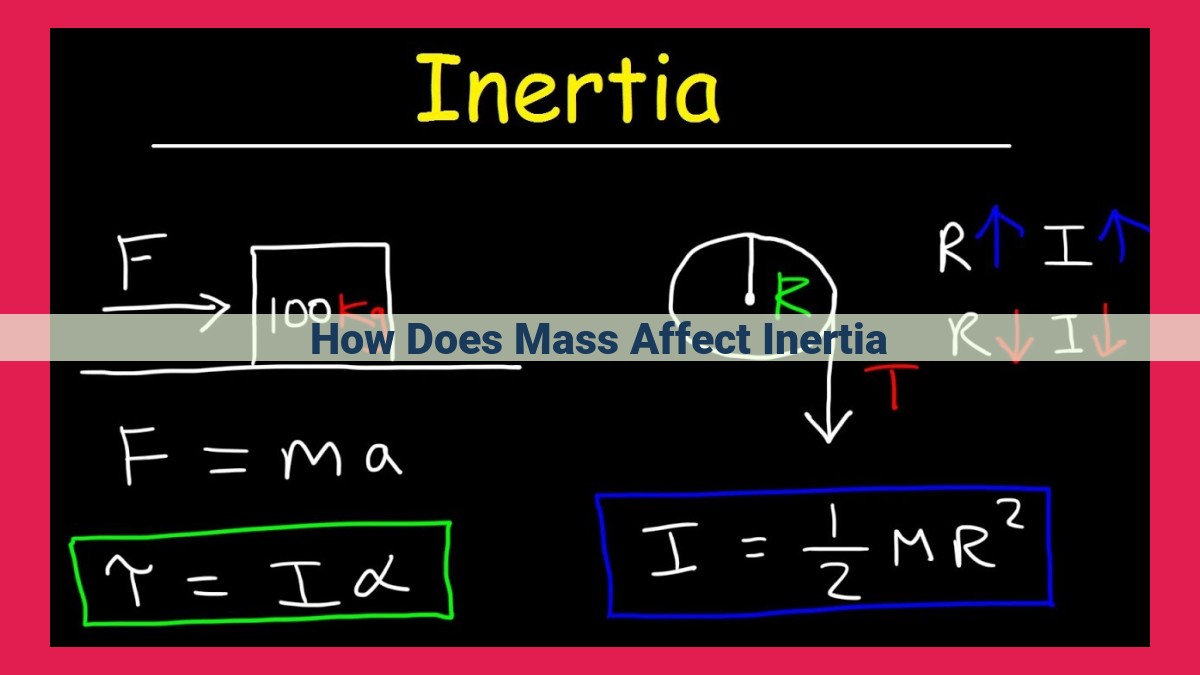
Mass significantly influences inertia, the resistance to changes in motion. According to Newton’s second law, force equals mass times acceleration (F = ma). This implies that an object with greater mass requires a greater force to accelerate or decelerate. Similarly, density, which is mass per unit volume, also affects inertia. Objects with higher density are more resistant to changes in motion due to their tightly packed molecules. By contrast, objects with lower density, like gases, have less inertia and are more easily accelerated.

Inertia and Momentum:

• Definition of inertia and its relation to momentum.

Inertia and the Unstoppable Force of Momentum

In the realm of physics, there exists a fascinating concept known as inertia, a property inherent to all matter. It is the reluctance of an object to change its state of motion, whether it’s at rest or moving. Inertia is directly related to momentum, a measure of an object’s motion that considers both its mass and velocity.

Imagine a bowling ball sitting still on the ground. Due to its inertia, it shows no intention of moving until an external force, such as a bowling ball launcher, acts upon it. This is where momentum comes into play. The launcher imparts momentum to the ball, causing it to accelerate and roll down the lane.

Inertia and momentum are like two sides of the same coin. Inertia is the resistance to change, while momentum is the force that overcomes that resistance. A more massive object possesses greater inertia, thus requiring a stronger force to alter its motion. Consider a large truck compared to a small car: the truck’s higher mass gives it more inertia, making it harder to accelerate or stop.

Understanding these concepts is crucial in explaining everyday phenomena. For instance, when you suddenly brake while driving, your body experiences a forward jolt due to inertia. The car’s mass wants to continue moving, but the brakes apply a force that opposes this motion, causing a change in momentum.

Inertia also plays a vital role in space exploration. It’s the reason why rockets need an immense amount of thrust to overcome the inertia of their massive payloads. Conversely, when astronauts return to Earth, they experience a gradual decrease in velocity as their spacecraft descends through the atmosphere. This is due to the air molecules exerting a force that opposes their motion, gradually reducing their momentum.

In summary, inertia is the property of matter that resists changes in motion, while momentum represents the combined effect of mass and velocity. Understanding these concepts provides invaluable insights into the behavior of objects in our physical world, from bowling balls rolling down lanes to rockets soaring through space.

Mass and Density: The Heavyweights of Inertia

In the realm of physics, the concepts of inertia and momentum reign supreme. Inertia, the resistance of an object to changes in its motion, is directly influenced by the object’s mass and density. In this section, we’ll delve into the fascinating relationship between mass, density, and the stubbornness of objects to either stay put or keep moving.

Mass: The Inertia Heavyweight

Mass, measured in kilograms, measures an object’s resistance to acceleration. The more massive an object, the more difficult it is to set it in motion or bring it to a stop. Think of a bowling ball versus a ping-pong ball. The bowling ball’s hefty mass means it requires a substantial force to get it rolling, and once it’s in motion, it’s hard to slow it down.

Density: The Density Advantage

Density, measured in kilograms per cubic meter, describes how tightly packed an object’s matter is. A dense object has more mass crammed into a smaller volume. For instance, a lead brick has a higher density than a wooden brick of the same size. This means that a lead brick has more inertia per unit volume, making it harder to accelerate or decelerate.

Inertia’s Direct Connection

Inertia is directly proportional to both mass and density. So, an object with both a large mass and high density will have the highest inertia. Imagine a massive piece of granite. Its high mass and density make it extremely difficult to move. In contrast, a large, fluffy cotton ball has low mass and low density, so it has very little inertia.

Consequences of Inertia

The inertia of an object has significant implications in the physical world. For example, it determines an object’s resistance to:

• Stopping: Cars with greater mass and density require longer stopping distances.
• Starting: Objects with higher inertia require more force to accelerate.
• Changing Direction: Objects with high inertia are more difficult to turn or maneuver.

Mass and density are crucial factors in understanding inertia. The more massive and dense an object, the greater its resistance to changes in motion. This knowledge is essential in various fields, from engineering and automotive design to sports science and even understanding the behavior of celestial bodies. By comprehending the principles of mass and density, we gain a deeper appreciation for the intricate workings of our physical world.

Newton’s First and Second Laws: Inertia and the Maintenance of Motion

Inertia: The Tendency to Resist Change

Imagine a bowling ball sitting motionless on the lane. It’s not moving because an invisible force called inertia is holding it back. Inertia is the property of matter that resists any change in its motion, whether it’s stationary or moving. A stationary object wants to stay still, and a moving object wants to keep moving at the same speed and direction.

Newton’s First Law: The Law of Inertia

This principle was first formulated by Sir Isaac Newton in his First Law of Motion, also known as the Law of Inertia. It states that an object at rest stays at rest, and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force.

Newton’s Second Law: The Law of Acceleration

However, if an unbalanced force is applied to an object, it will accelerate. Newton’s Second Law of Motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This means that the greater the force applied, the greater the acceleration; and the more massive the object, the less the acceleration.

Overcoming Inertia

To overcome inertia, the net force acting on an object must be greater than zero. This can be achieved by applying a force in the desired direction of motion, such as pushing a bowling ball down the lane. The greater the force applied, the greater the acceleration imparted to the object, and the more quickly it will overcome its inertia and start moving.

Maintaining Motion

Once the object is moving, inertia will continue to resist any changes in its motion. If no external force is applied, it will continue moving at the same speed and in the same direction indefinitely. This is known as the law of conservation of momentum.

Practical Applications

Newton’s First and Second Laws have countless practical applications in everyday life and engineering. From the motion of vehicles to the design of spacecraft, understanding the role of inertia and acceleration is crucial for understanding and predicting the behavior of objects in motion.

Law of Conservation of Momentum: Where Motion and Inertia Dance

In the fascinating world of physics, momentum reigns supreme, governing the movement and interaction of objects. Imagine a lively dance floor where colliding dancers represent objects in motion. Each dancer possesses a unique momentum, a combination of their mass and velocity.

As the dancers twirl and glide across the floor, the Law of Conservation of Momentum dictates that the total momentum of the system remains constant. This means that when dancers collide, their combined momentum is not lost or gained but simply transferred.

This transfer of momentum translates into changes in the dancers’ inertia. Inertia is the property of an object that resists changes in its motion. The more massive an object, the greater its inertia and the harder it is to stop or accelerate.

When dancers collide, the dancer with greater inertia will have a smaller change in velocity, while the dancer with less inertia will experience a greater change, such that the total momentum remains the same.

This principle is not limited to the dance floor. It governs all collisions in the universe, from microscopic interactions to cosmic events. In car accidents, for instance, the total momentum of the vehicles remains constant before, during, and after the collision. This helps explain the severity of the impact and the forces involved.

By understanding the Law of Conservation of Momentum, we gain a deeper appreciation for the intricate mechanics of motion and the dance-like nature of the physical world. It reminds us that even in the most chaotic of collisions, the total momentum is preserved, a testament to the underlying order and balance that govern our universe.

Force and Impulse: Shaping Inertia’s Fate

Force: The Invisible Hand that Pushes and Pulls

Force, a ubiquitous entity in our world, is the catalyst that alters the destiny of inertia. It’s the invisible hand that pushes and pulls objects, setting them in motion or bringing them to a standstill. From the gentle breeze rustling leaves to the colossal impact of a meteor, force governs the dance of objects.

Impulse: A Transient Surge of Force

Impulse is force’s transient accomplice, delivering a concentrated burst of energy that modifies an object’s inertia. Think of it as a sudden jolt that, like a lightning strike, can drastically alter an object’s momentum. Collision, for instance, is a vivid showcase of impulse in action, where two objects collide, exchanging a surge of force that changes their respective states of motion.

Modifying Inertia: A Dynamic Dance

Force and impulse, like skilled choreographers, orchestrate the graceful ballet of inertia. Force, with its relentless push or pull, imparts momentum to objects, setting them into motion. Conversely, impulse delivers a concentrated burst of force, abruptly altering an object’s momentum, causing it to speed up, slow down, or change direction. In the realm of physics, this interplay between force, impulse, and inertia is a captivating tango that governs the motion of everything around us.

Acceleration and Velocity: A Dance of Mass and Inertia

Inertia, that stubborn resistance to change, finds its dance partner in velocity, the measure of motion’s speed and direction. Together, they waltz through the realm of physics, with mass as their choreographer.

Mass, the quantity of matter in an object, is like a hefty dance partner. The more mass an object has, the more reluctant it is to accelerate. Picture a massive boulder being pushed along a path. Its inertia resists the force, making it seem to move sluggishly, like a reluctant dancer.

Acceleration, the rate at which velocity changes, is the force that tries to change inertia’s sway. It’s like a persistent suitor, nudging the object to move faster or slower, change direction, or even come to a halt.

The interplay between mass and acceleration reminds us of Newton’s second law of motion: force equals mass times acceleration. As force, the external push or pull on an object, increases, so too does acceleration. This is why a heavier object requires more force to accelerate at the same rate as a lighter one.

Velocity, the object’s speed and direction, is a direct consequence of acceleration. As acceleration pushes the object along, its velocity changes accordingly. Imagine a spinning top. As it accelerates, its speed increases, and its direction of spin changes.

Momentum, the product of mass and velocity, keeps track of the dance’s intensity. It’s like a measure of how much the object wants to keep moving. A change in momentum means either mass or velocity has changed, which can be caused by an outside force.

So, there we have it: inertia’s resistance, acceleration’s push, mass’s weightiness, and velocity’s direction intertwine in a captivating dance. Understanding this interplay is crucial for grasping the movement of objects in our universe.