Exterior Angle Theorem: Understanding Same-Side Exterior Angles And Their Significance
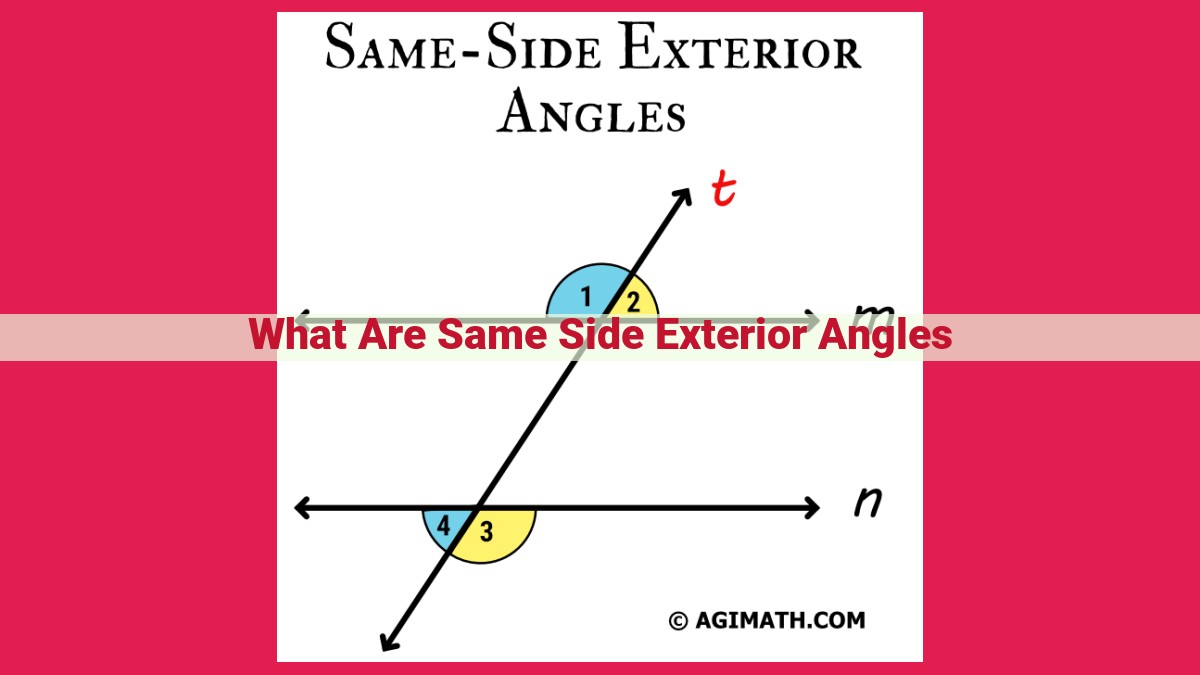
Same side exterior angles are formed when a transversal intersects two lines, forming angles outside the lines on the same side. These angles are related to the interior angles and are significant in geometry. They have a special relationship with consecutive interior angles, where the exterior angle is equal to the sum of the non-adjacent interior angles. This is known as the Exterior Angle Theorem. Same side exterior angles are crucial for understanding relationships between angles and lines, and have practical applications in fields such as architecture and surveying.
Same Side Exterior Angles: A Comprehensive Guide
In the realm of geometry, angles play a vital role in understanding shapes and relationships. Among these angles, same side exterior angles hold a special place, offering insights into the dynamics of intersecting lines. Let’s embark on a journey to unravel their definition and significance.
Defining Same Side Exterior Angles
Imagine two lines, l and m, intersecting at a point, O. When a third line, t, known as the transversal, intersects both l and m on the same side, the angles formed are known as same side exterior angles. These angles are named according to their relationship with the intersecting sides and the transversal.
Relationship to Adjacent Sides and the Transversal
Angle 1 lies in the exterior of angle 4, adjacent to side l, and on the same side of the transversal t. Similarly, angle 3 lies in the exterior of angle 2, adjacent to side m, on the same side of t.
These angles play a crucial role in understanding the relationship between the intersecting lines and the transversal. By analyzing their measurements and properties, we can gain insights into the geometry of the figure as a whole.
Consecutive Interior and Exterior Angles:
- Explore the connection between consecutive interior angles and the exterior angle on the same side of the transversal.
Consecutive Interior and Exterior Angles: A Tango on a Transversal
Imagine a transversal, like a mischievous dance partner, intersecting two parallel lines. This encounter creates a captivating interplay of angles, where consecutive interior angles and the exterior angle on the same side of the transversal share a secret connection.
Let’s picture this dance floor. The transversal plays the role of the divider, cleaving a path through the parallel lines. On one side, we have two interior angles, nestled next to each other like inseparable friends. These consecutive interior angles are formed by the parallel lines and the transversal.
On the other side of the transversal, like an enigmatic loner, stands the exterior angle. This angle is formed outside the parallel lines and the transversal. It’s like the rebellious cousin of the interior angles, daring to break away from the norm.
The Intimate Connection
The connection between consecutive interior angles and the exterior angle is like a secret pact, a whispered understanding. This pact is known as the Exterior Angle Theorem. It states that the exterior angle is equal to the sum of the opposite, non-adjacent interior angles.
In other words, the exterior angle is a generous soul, sharing its angular wealth with the interior angles on the opposite side of the transversal. This theorem is like a dance step, a harmonious exchange between these seemingly disparate angles.
A Real-Life Analogy
Imagine a construction worker measuring the angles of a rectangular building. To measure the exterior angle, they wouldn’t need a separate measurement. Instead, they could simply add the two opposite interior angles. This is because of the Exterior Angle Theorem, the secret pact between consecutive interior angles and the exterior angle.
The connection between consecutive interior angles and the exterior angle is like a guiding star for understanding angles on a transversal. It’s a testament to the hidden harmonies and relationships that exist within the world of geometry. By embracing this concept, we unlock a deeper appreciation for the intricate and elegant dance of angles on a transversal.
Relationship Between Exterior and Interior Angles: Unveiling the Mathematical Connection
Imagine you’re strolling through a beautiful park, captivated by the intricate patterns formed by the crisscrossing paths. Each path intersects with another, creating a fascinating interplay of angles. Among these angles, a special type stands out—the same side exterior angle.
An exterior angle is formed when two lines intersect, and the angle is located outside the intersecting lines. A same side exterior angle occurs when two lines intersect and the exterior angle lies on the same side as an interior angle.
To understand the connection between same side exterior angles and interior angles, let’s delve into the Exterior Angle Theorem. This theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles.
Let’s clarify this theorem with a triangle ABC. The exterior angle ∠BCD is formed when line segment BC intersects transversal BD. The remote interior angles are ∠ABC and ∠BCA. According to the Exterior Angle Theorem, we have:
∠BCD = ∠ABC + ∠BCA
This formula reveals the mathematical relationship between exterior angles and interior angles. It establishes that an exterior angle is equal to the sum of the two non-adjacent interior angles on the same side of the transversal.
This connection is fundamental in geometry. It allows us to solve various angle measurement problems and understand the properties of triangles. So, next time you’re admiring the geometric beauty of your surroundings, remember the Exterior Angle Theorem—a key to unlocking the secrets of angle relationships.
Identifying Same Side Exterior Angles in Diagrams
Same side exterior angles are fascinating mathematical concepts that hold the key to understanding various angle relationships. Visualizing these angles can be tricky at first, but with a step-by-step guide and diagrams, you’ll find it a piece of cake.
Step 1: Locate the Transversal
Imagine a straight line, called a transversal, intersecting two other straight lines, forming four angles.
Step 2: Identify the Exterior Angle
An exterior angle is the angle outside the two lines formed by the transversal. In this case, look for the angle that is outside the two intersected lines.
Step 3: Choose a Non-Adjacent Interior Angle
From the two angles formed inside the intersected lines, choose one that is not adjacent to the exterior angle. This is the non-adjacent interior angle.
Step 4: Verify the Same Side
Ensure that the exterior angle and the non-adjacent interior angle are on the same side of the transversal. If they are, you have found a pair of same side exterior angles.
Example Diagram:
[Diagram of two lines intersected by a transversal, showing exterior angle and non-adjacent interior angle on same side]
In the diagram, ∠EDC is the exterior angle and ∠BCA is the non-adjacent interior angle. They are on the same side of the transversal, making them a pair of same side exterior angles.
Same Side Exterior Angles: Real-World Examples
Understanding same side exterior angles is not just limited to textbook diagrams. Let’s explore a few captivating real-world examples that will solidify your comprehension of this geometrical concept.
First, let’s revisit the definition. Same side exterior angles are those formed when a transversal (a line that intersects two other lines) passes through the exterior of two lines, on the same side. Imagine a railroad track where two lines intersect, forming an “X”. The four angles outside the intersection are same side exterior angles.
To differentiate them from other angles, remember that same side exterior angles always share the same vertex. For instance, in our railroad analogy, the angles at the top and bottom points of the “X” are same side exterior angles. They share the vertex at the intersection point.
Consider this example: A farmer measures the angle between two adjacent fences (let’s call them line 1 and line 2) to be 100 degrees. A road (transversal) crosses both fences at the same point. The angle formed outside line 1 and opposite to the 100-degree angle (let’s call it angle A) is a same side exterior angle. The angle formed outside line 2 and opposite to angle A (angle B) is also a same side exterior angle.
Here’s where it gets interesting: The sum of angles A and B is 180 degrees. This is known as the Exterior Angle Theorem. It’s a handy rule that helps us find the measure of same side exterior angles.
In our farmer’s example, since the interior angle is 100 degrees, each same side exterior angle (angle A and angle B) would be (180 – 100) / 2 = 40 degrees.
These real-world examples not only strengthen your understanding of same side exterior angles but also provide a glimpse into the practical applications of geometry in various fields, such as architecture and surveying.
Theorems on Same Side Exterior Angles: Unveiling the Relationship between Exterior and Interior Angles
In the realm of geometry, angles play a pivotal role in understanding the properties and relationships of shapes. Same side exterior angles, in particular, hold a special significance in this geometric landscape. These angles are formed when two parallel lines are intersected by a transversal, and understanding the theorems associated with them deepens our grasp of angle relationships.
One of the most fundamental theorems governing same side exterior angles is the Exterior Angle Theorem. This theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles on the same side of the transversal. In other words, if an exterior angle is formed by extending one side of a triangle, it will be equal to the sum of the angles opposite the other two sides of the triangle.
This theorem has profound implications in various geometric constructions and proofs. For instance, it can be used to find the measure of an unknown interior angle of a triangle if the measures of the other two interior angles and the exterior angle are known. Additionally, the Exterior Angle Theorem is crucial in proving theorems related to parallel lines and transversals, such as the Same Side Interior Angle Theorem and the Alternate Interior Angle Theorem.
Another significant theorem associated with same side exterior angles is the Angle Addition Postulate. This postulate states that the sum of the measures of the three angles in a triangle is always equal to 180 degrees. By combining this postulate with the Exterior Angle Theorem, we can derive a powerful formula that relates an exterior angle to a non-adjacent same side interior angle. The formula states that the measure of an exterior angle is equal to 180 degrees minus the measure of the non-adjacent interior angle.
These theorems provide a solid foundation for understanding the intricate relationships between exterior and interior angles in geometric figures. They serve as essential tools for solving geometric problems, constructing proofs, and unraveling the mysteries of the geometric world.
Applications of Same Side Exterior Angles
Understanding same side exterior angles finds its way into various practical applications. Let’s explore how this concept aids professionals in the field:
Architecture and Design:
In architecture, precision and accuracy are paramount. Same side exterior angles play a crucial role in determining the angles of walls, roofs, and other structural elements. By measuring and calculating these angles, architects can ensure that buildings are structurally sound and aesthetically pleasing.
Surveying and Mapping:
Surveyors rely on same side exterior angles to determine the shape and size of land parcels and geographical features. Using a transit or theodolite, they measure the angles between different points and use the properties of same side exterior angles to calculate the distances and areas of the surveyed area. This information is essential for land ownership, boundary disputes, and planning purposes.
Construction and Engineering:
In construction and engineering, it’s essential to align structural components accurately. Same side exterior angles provide a precise method for measuring and setting the angles of beams, columns, and other elements. This ensures proper alignment, structural stability, and optimal performance of the entire structure.