Understanding Cosine Wave Period: The Ultimate Guide
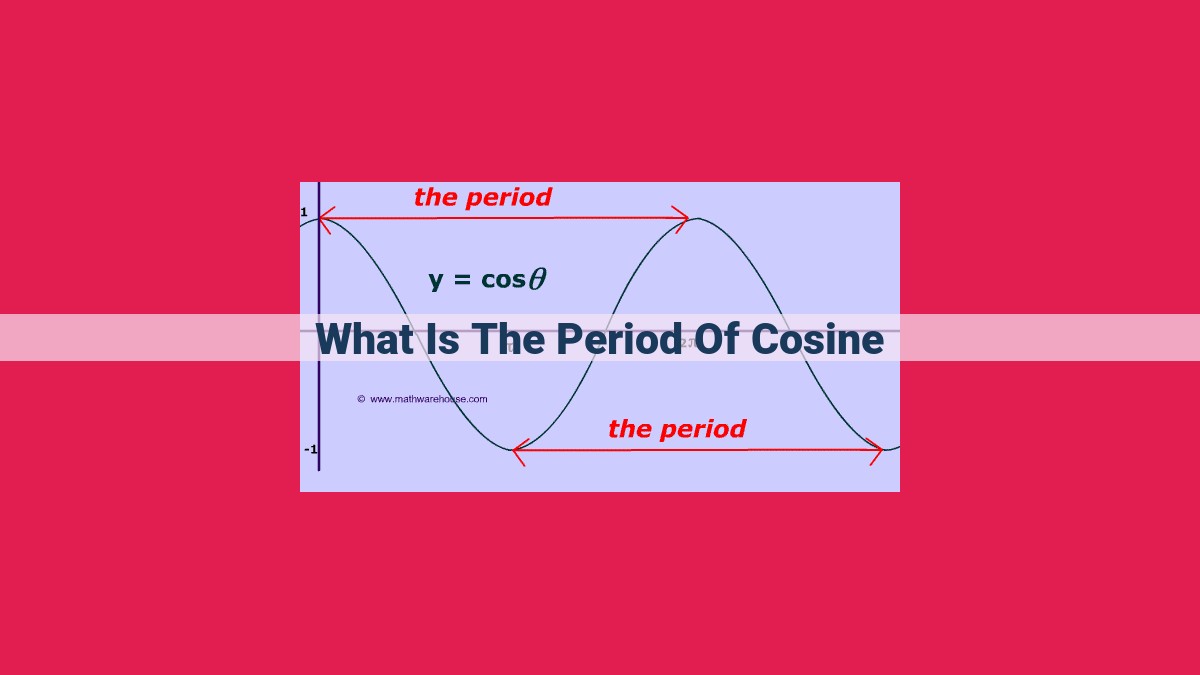
The period of a cosine wave is the time it takes for one complete cycle, from the maximum positive value to the minimum negative value and back to the maximum positive value. It is measured in seconds. The period of a cosine wave is inversely proportional to its frequency, which is the number of cycles per second. The period is also directly proportional to the wavelength, which is the distance between two consecutive crests or troughs of the wave.
Delving into the Heart of a Cosine Wave: Understanding Its Period
In the realm of waves, the period holds immense significance. It’s the temporal rhythm that dictates how often a wave’s pattern repeats itself. Think of it as the heartbeat of the wave, determining its distinctive characteristics. Delving into the concept of a cosine wave’s period will unveil the secrets behind its rhythmic nature.
A cosine wave is a graceful undulation that traces a sinusoidal pattern, smoothly oscillating around its mean position. Its period, denoted by the letter T, measures the time it takes for the wave to complete one full cycle—from its peak, through its trough, and back to its peak again. This fundamental property defines the wave’s characteristic frequency, which is expressed in units of cycles per second, or Hertz (Hz).
Comprehending the period of a cosine wave gives us a window into understanding the wave’s overall behavior. It reveals the rate at which the wave oscillates and provides valuable insights into its dynamics. Equipped with this knowledge, we can analyze and interpret various wave phenomena, from the rhythmic swaying of a pendulum to the propagation of sound waves through the air.
Frequency and Wavelength: The Heartbeat of a Cosine Wave
Picture a glistening lake on a calm evening. As the sun begins its descent, gentle ripples dance across the water’s surface. These ripples embody the essence of a cosine wave, an oscillating pattern that governs countless phenomena in our world.
Central to a cosine wave is its frequency, measured in hertz (Hz). Frequency refers to the number of cycles – complete up-and-down oscillations – that the wave completes per second. A high-frequency wave oscillates rapidly, like the rapid vibrations of a guitar string. Conversely, a low-frequency wave moves more leisurely, similar to the gentle undulations of a flag in the breeze.
Intertwined with frequency is wavelength, denoted in meters (m). Wavelength represents the distance between two consecutive peaks (crests) or troughs of the wave. A short wavelength indicates that the wave’s peaks and valleys are packed close together, like the ripples on a choppy sea. In contrast, a long wavelength means that the wave has more space between its peaks and troughs, akin to the stately swells of the ocean.
In the tapestry of a cosine wave, frequency and wavelength dance in perfect harmony. A high-frequency wave invariably has a short wavelength, while a low-frequency wave pairs with a long wavelength. This interconnected relationship forms the backbone of wave propagation.
Unveiling the Interplay of Period, Frequency, and Wavelength in a Cosine Wave
In the tapestry of waves, the cosine wave stands out, its rhythmic oscillations providing a foundation for understanding wave phenomena. Among its defining characteristics, period, frequency, and wavelength form an intricate dance, each influencing the other in a harmonious resonance.
Period (T): The period of a wave is the duration of one complete oscillation, from one peak (crest) to the next or one trough to the next. It is measured in seconds. The period dictates how slowly or quickly the wave repeats itself.
Frequency (f): Frequency measures how often a wave repeats itself within a given time frame. It is expressed in cycles per second, also known as Hertz (Hz). A higher frequency corresponds to more oscillations per unit time, resulting in a faster-varying wave.
Wavelength (λ): The wavelength represents distance between two consecutive crests or troughs of a wave. It is measured in meters. A larger wavelength indicates a longer distance between wave undulations, resulting in a more spread-out wave.
The relationship between period, frequency, and wavelength is elegantly captured by the equation T = 1/f = λ/v, where v is the wave velocity. This equation reveals that period, frequency, and wavelength are inversely proportional.
T = 1/f: As the frequency increases, the period decreases. This means that a faster-repeating wave (higher frequency) has a shorter duration between oscillations.
T = λ/v: Period is also directly proportional to wavelength. A longer wavelength corresponds to a larger distance between crests or troughs, leading to a longer duration of one oscillation.
By understanding the interplay between period, frequency, and wavelength, we unlock the key to interpreting and analyzing cosine waves. This knowledge empowers us to unravel the mysteries of wave phenomena across various disciplines, from acoustics and engineering to medicine.
Amplitude and Phase Shift: The Heart of Cosine Wave Characteristics
In the world of cosine waves, amplitude and phase shift play pivotal roles in shaping their unique behaviors. Amplitude, measured in meters, represents the wave’s maximum displacement from its mean position. It determines the wave’s height and intensity.
Phase shift, on the other hand, refers to the horizontal displacement of a wave from a reference wave. It indicates the starting point of the wave’s oscillation relative to the reference. Visualize it as a slight shift to the right or left, like a dancer starting their performance off-beat.
Unveiling Phase Shift: Initial Phase and Delay
Phase shift is often characterized by two key parameters: initial phase and delay. Initial phase defines the wave’s position at the instant of measurement, while delay indicates the wave’s tardiness compared to the reference wave. A positive initial phase implies an early start, while a negative phase signifies a late arrival.
Practical Applications: Cosine Waves in the Real World
The understanding of amplitude and phase shift extends beyond theoretical concepts. These characteristics find practical applications in diverse fields. In acoustics, they shape the timbre of musical instruments. In engineering, they optimize signal processing and communication systems. Even in medicine, cosine waves play a role in analyzing brain activity through electroencephalography (EEG).
By delving into the intricacies of amplitude and phase shift, we uncover the hidden language of cosine waves. These parameters orchestrate the wave’s behavior, enabling us to harness their power in a myriad of applications that enhance our understanding of the world around us.
Interpretation of Phase Shift: Unveiling the Secrets of Time and Space
In the realm of waves, the phase shift is a crucial concept that unlocks the secrets of time and space. It represents the initial phase of a wave, which determines its starting point in its cyclical journey. Phase shift can manifest as a delay or a shift in the wave’s movement, creating distinctive patterns that reveal important information about the wave’s behavior.
Understanding Initial Phase
Every wave possesses an initial phase, which defines the starting point of its cycle. This phase angle is measured in degrees or radians and establishes the wave’s position relative to a reference point. It determines the timing of the wave’s motion, influencing when crests and troughs appear.
Delay and Shift: A Tale of Time
Phase shift can manifest as a delay or a shift in the wave’s movement. A positive phase shift indicates that the wave has been delayed compared to a reference wave, while a negative phase shift suggests that the wave has shifted earlier. These delays and shifts provide valuable insights into the time relationships between different waves or between different points on a single wave.
Unlocking the Secrets of Space
Phase shift also unveils the mysteries of space. By comparing the phase shift between two waves, we can determine the distance between two points on the wave. This principle finds application in techniques such as holography and interferometry, where phase shift analysis reveals the depths and shapes of objects.
The interpretation of phase shift empowers us to decipher the intricate dance of waves. By understanding the initial phase, delay, and shift, we unravel the secrets of time and space, gaining deeper insights into the behavior and applications of waves in diverse fields such as acoustics, engineering, and medicine.
Applications of the Cosine Wave:
- Examples of the practical applications of cosine waves in various fields (e.g., acoustics, engineering, medicine).
Applications of the Cosine Wave
Cosine waves, characterized by their smooth, periodic oscillations, find wide-ranging applications across various fields. These include:
Acoustics:
Cosine waves form the basis of sound waves, which are longitudinal disturbances that travel through a medium. The frequency of a cosine wave corresponds to the pitch of the sound, while its amplitude determines the loudness.
Engineering:
In engineering, cosine waves are used for signal processing, control systems, and vibration analysis. For example, in signal processing, cosine waves are employed as carrier signals for data transmission.
Medicine:
In medicine, cosine waves are used in electrocardiograms (ECGs), which measure the electrical activity of the heart. The shape and frequency of the cosine waves in an ECG can indicate various heart conditions.
Other Applications:
Beyond these major fields, cosine waves also have applications in:
- Radio communications: As modulating waves for transmitting data
- Computer science: For data compression and image processing
- Finance: For modeling financial time series and forecasting trends
The versatility of cosine waves stems from their ability to represent periodic phenomena. By understanding the period, frequency, wavelength, amplitude, and phase shift of a cosine wave, scientists and engineers can harness its power for a variety of practical applications.