Uncover The Essence Of Amplitude: Understanding Its Impact On Function Graphs

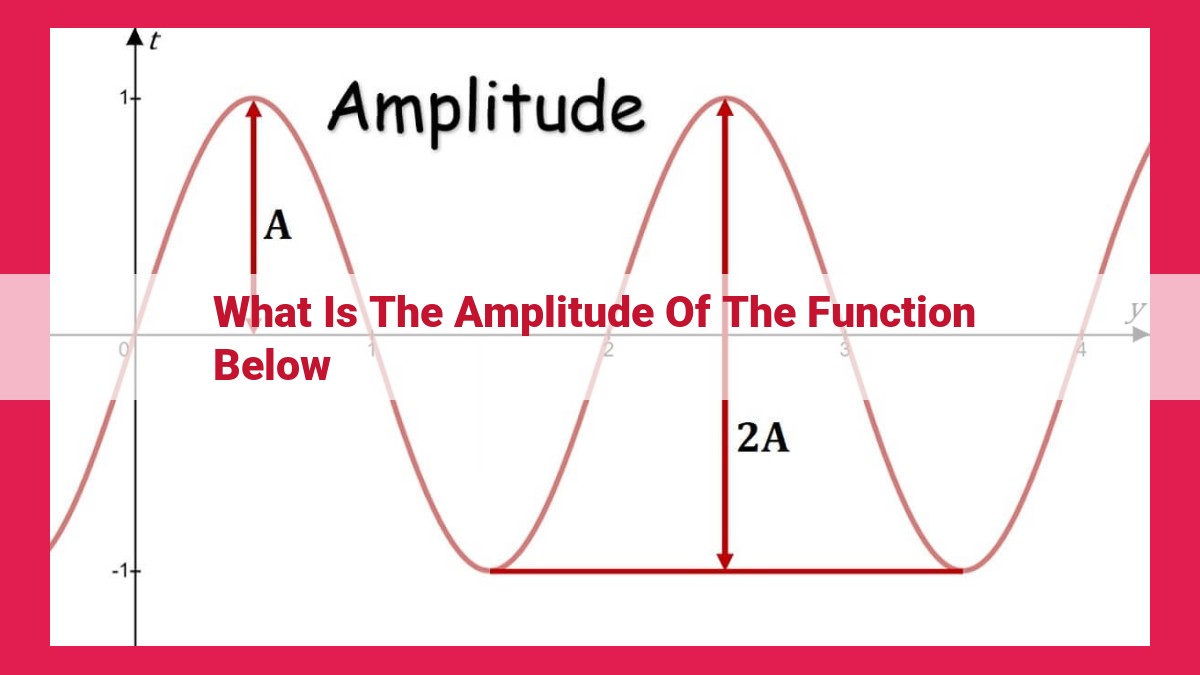
Amplitude, in the context of functions, represents the distance from the midline (a horizontal axis representing the average value) to the maximum or minimum value of the function. It signifies the extent of the oscillation or variation in the function’s graph. Amplitude is related to the distance from the midline to the absolute maximum (highest point) or absolute minimum (lowest point). It is influenced by the function’s period (frequency of oscillations), and its value is often indicated in the function’s equation. Vertical translations affect the position of the midline but preserve the amplitude, as the distance from the new midline to maximum and minimum values remains constant. Analyzing amplitude provides insights into the behavior and characteristics of functions.

Amplitude: The Pulse of Functions

Amplitude, like the heartbeat of a function, plays a vital role in understanding its behavior. It measures the extent or magnitude of the function’s oscillations.

Imagine a swing set in motion. The height of the swing at its highest point represents the maximum value of the function, while the lowest point represents the minimum value. Amplitude is the distance from the midline (the horizontal axis of symmetry) to either the maximum or minimum point. Understanding amplitude helps us analyze functions and appreciate their unique characteristics.

Amplitude and Related Concepts: Unraveling the Symphony of Functions

In the world of functions, understanding amplitude is akin to grasping the heartbeat that animates their ebb and flow. Amplitude embodies the magnitude of change from the midline, the axis around which functions oscillate.

Maximum and Minimum Values: The Crest and Trough of Peaks and Valleys

Maximum and minimum values represent the highest and lowest points a function can reach, respectively. The distance between these points and the midline determines the amplitude. This distance embodies the range of oscillations, a measure of how extreme the function’s variations can be. Furthermore, functions may possess absolute maximum and absolute minimum values, representing their overall highest and lowest points within a specified domain.

Period: The Tempo of Oscillations

Period measures the repetition length of a function’s oscillations. It dictates the frequency of these oscillations, influencing how many times a function completes a cycle within a given interval. The higher the period, the slower the oscillations and the lower the frequency. Conversely, a shorter period implies a higher frequency, resulting in more frequent oscillations.

Midline: The Center of the Stage

The midline serves as the reference point for amplitude measurements. It represents the horizontal line about which a function oscillates. Vertical shifts of a function translate the entire graph up or down, effectively altering the midline’s position but preserving the amplitude.

Function Notation: Decoding the Amplitude in Algebraic Shorthand

Amplitude is often denoted by the letter “A” in a function’s equation. For instance, in the equation f(x) = A * sin(x), the value of “A” represents the amplitude of the sine function. Understanding how amplitude is expressed in function notation allows for quick interpretation of its value.

Vertical Translation and Amplitude: The Interplay of Ups and Downs

In the world of functions, amplitude plays a pivotal role in shaping the ups and downs of our mathematical landscapes. Just as in music, where amplitude determines the volume of a sound, in functions, it dictates the vertical extent of oscillations. But when we introduce vertical translation, the interplay between these concepts becomes even more fascinating.

Preserving Amplitude: A Vertical Shift with No Distortion

Think of vertical translation as a shift that moves the entire function up or down, like shifting a graph vertically on a coordinate plane. Remarkably, this translation preserves the amplitude of the function. The distance between the maximum and minimum values of the function remains unchanged, ensuring that the shape and size of its oscillations are unaffected.

Why Preserved Amplitude Matters

Understanding the preservation of amplitude is crucial because it allows us to interpret functions even after they have been translated vertically. Whether a function is shifted up or down, its amplitude retains its original value, giving us insights into the underlying characteristics of the function.

Visualizing Vertical Translation

Imagine a sinusoidal function, a graceful wave-like curve. When we translate it vertically upward, the entire curve moves upward, maintaining its shape and amplitude. Similarly, a downward translation shifts the curve downward, preserving its amplitude. It’s like taking a mold of the original function and placing it at a different height without altering its dimensions.

Practical Applications

The interplay between vertical translation and amplitude has real-world applications in various fields. In engineering, it helps us understand the vibration patterns of structures. In medicine, it aids in analyzing heart rate variability and other physiological signals. By comprehending the preservation of amplitude, we gain deeper insights into these complex systems.

Amplitude: The Foundation for Function Analysis

Understanding Amplitude: The Rise and Fall of Functions

Amplitude is the key to unraveling the secrets of functions. Like a heartbeat or the ebb and flow of the tides, amplitude measures the distance from the midline to the maximum or minimum values of a function. It quantifies the height of the function’s peaks and the depth of its valleys, revealing the function’s rhythm and pattern.

Related Concepts: A Symphony of Mathematical Measures

Amplitude doesn’t exist in isolation. It intertwines with other concepts to paint a comprehensive picture of a function’s behavior.

• Period: The period determines how often the function’s pattern repeats itself, influencing the amplitude’s frequency.
• Midline: The midline represents the center point around which the function oscillates, affecting the amplitude’s vertical position.
• Function Notation: Amplitude is often symbolized by the letter “A” in function equations, signifying its importance.

Vertical Translation and Amplitude: A Delicate Dance

When a function is vertically translated, its amplitude remains unchanged. Vertical shifts only move the function up or down, preserving the distance between the midline and the maximum or minimum values.

Example: Unraveling Amplitude in the Wild

Consider the function f(x) = 2sin(x) – 1.

• Amplitude: 2
• Period: 2π
• Midline: y = -1

The amplitude of 2 indicates that the function oscillates 2 units above and below its midline, creating a wave pattern with a maximum value of 1 and a minimum value of -3.

Amplitude is the compass by which we navigate the complexities of functions. By understanding amplitude and its interconnected concepts, we gain a deeper insight into the functions that shape our world. Whether it’s modeling the rhythmic cycles of nature or analyzing the behavior of complex systems, amplitude empowers us to unlock the secrets of mathematics and make sense of the world around us.