Understanding Acute Triangles: Properties And Characteristics

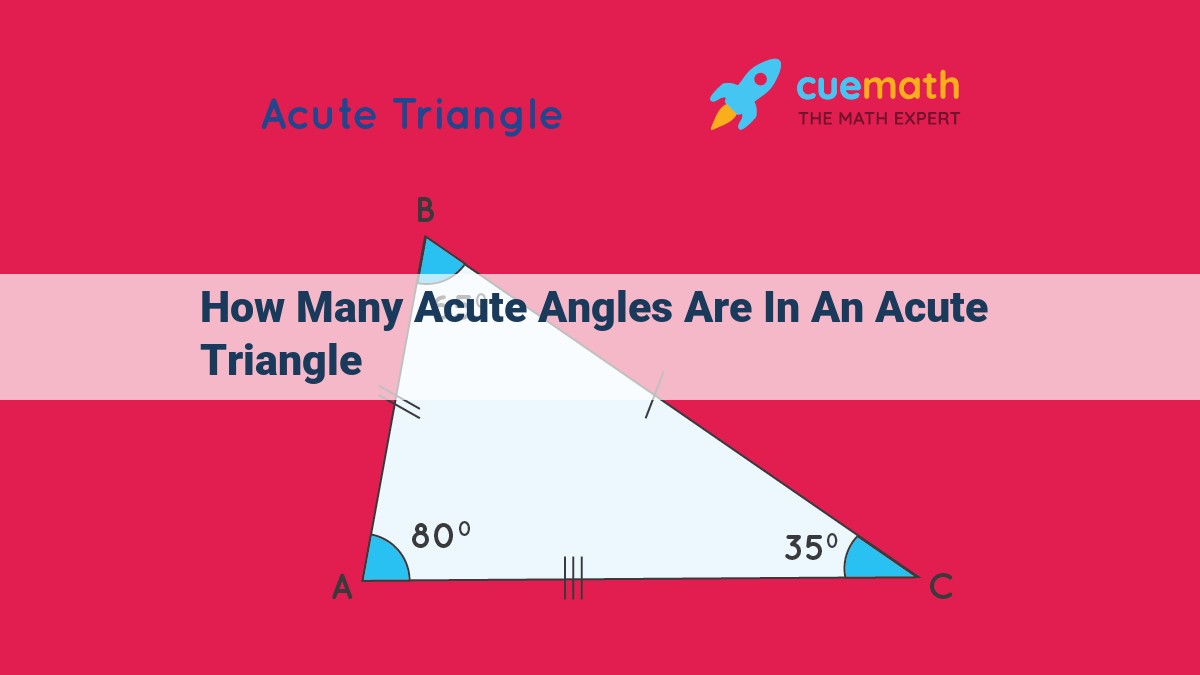
An acute triangle, defined by its three interior angles being all less than 90 degrees, possesses three acute angles. This is because the sum of the interior angles of any triangle equals 180 degrees, and since an acute angle is less than 90 degrees, the remaining two angles must also be acute to maintain the 180-degree sum.

• Define an acute triangle and its characteristics.
• State the purpose of the blog post: to determine the number of acute angles in an acute triangle.

Acute Triangles: Unveiling the Secrets of their Angles

In the realm of geometry, triangles take center stage as fascinating shapes with a captivating array of properties. Among these triangles, acute triangles stand out for their unique characteristic: all three interior angles are acute. But hold on a moment, what exactly are acute angles, and how many do acute triangles possess? Join us on this mathematical adventure as we delve into the world of acute triangles to uncover the secrets behind their angular treasures.

Unveiling the Essence of Acute Angles

Before we delve into the world of acute triangles, let’s first unpack the concept of an acute angle. An acute angle, my dear reader, is an angle less than 90 degrees. These angles are often depicted as sharp and narrow, distinct from their wider counterparts, right angles, and even more expansive obtuse angles.

Defining Acute Triangles: A Geometric Masterpiece

Now, let’s turn our attention to the enigmatic acute triangle. An acute triangle is a triangle in which all three interior angles are acute. In other words, each angle measures less than 90 degrees. This geometric marvel stands in contrast to its counterparts, right triangles and obtuse triangles, which possess one or more angles measuring exactly 90 degrees or greater than 90 degrees, respectively.

Unveiling the Number of Acute Angles in an Acute Triangle

So, here’s the million-dollar question: How many acute angles does an acute triangle harbor? The answer, my fellow geometry enthusiasts, is three. That’s right, every single interior angle in an acute triangle is acute. Why is that? Well, the sum of the interior angles of any triangle is always 180 degrees. Since acute triangles only have acute angles, each angle must measure less than 180 degrees. And since there are three angles, they must all be less than 90 degrees, making them all acute.

To summarize our thrilling expedition into the world of acute triangles, we have discovered that these captivating geometric shapes possess three acute angles, each measuring less than 90 degrees. This unique characteristic sets them apart from other triangle types and plays a crucial role in their properties and characteristics. Understanding the number of acute angles in an acute triangle is essential for unlocking a deeper comprehension of these mathematical wonders and their intriguing behaviors.

Concept 1: Acute Angle

Angle: A Dancer’s Twist and Turn

Imagine a dancer twirling on stage, her graceful movements creating arcs in the air. These arcs divide space into different sections, and just as dancers have a range of twirls and turns, so too do these arcs form angles of varying sizes.

Acute Angle: The Dancer’s Petite Step

Amongst the plethora of angles, the acute angle is the dancer’s petite step, a modest turn that measures less than 90 degrees. Like a ballerina’s delicate plie, an acute angle is a gentle bend, a mere whisper of a twirl.

Protractor: The Angle Ruler

To measure these angles, we call upon the protractor, a trusty tool that resembles a dancer’s outstretched arms. Its graduated markings precisely determine the angle’s degree, the amount of bend or twist in our dancer’s graceful arc.

Degrees: The Language of Angles

The unit of measurement for angles is the degree, a dancer’s eloquent language that precisely describes the extent of her turn. With 360 degrees marking a full circle, the acute angle occupies less than half of this circle, its gentle bend measured in degrees below 90.

Triangle: A Geometric Marvel

In the realm of geometry, triangles reign supreme as one of the fundamental building blocks. Let’s delve into the fascinating world of triangles and unravel their intriguing properties.

A triangle can be defined as a closed two-dimensional figure formed by three straight lines that meet and intersect at three distinct points, called vertices. These lines are known as sides, and the points where they meet are known as angles.

Triangles come in various shapes and sizes, and they can be classified based on the lengths of their sides and the measures of their angles. Let’s explore the different types of triangles:

Equilateral Triangles

Equilateral triangles are the most symmetrical and regular type of triangle. All three of their sides are congruent, meaning they have equal lengths. As a result, all three angles are also congruent and measure 120 degrees.

Isosceles Triangles

Isosceles triangles have two congruent sides and two congruent angles. The base angle, which is the angle opposite the non-congruent side, is equal to the other two “base angles”.

Scalene Triangles

Scalene triangles have no congruent sides and no congruent angles. They are the most diverse type of triangle, as their sides and angles can vary greatly in size and measure.

Understanding the different types of triangles is essential for comprehending their unique properties and relationships. They play a significant role in the broader field of geometry and have numerous applications in architecture, engineering, and real-world scenarios.

Concept 3: Interior Angles of a Triangle

When we venture into the world of triangles, we encounter a fascinating mathematical property. Every triangle, no matter its shape or size, holds a secret harmony within its angles.

The sum of the interior angles of any triangle is always 180 degrees. This unwavering rule governs all triangles, creating a delicate balance between their angles. It’s like a magical equation that holds the triangle together, keeping it in perfect equilibrium.

Now, let’s think about acute triangles. These triangles are special because all three of their angles are less than 90 degrees. How does this fact connect to the sum of interior angles?

Well, since the sum of the interior angles is always 180 degrees, and all three angles of an acute triangle are less than 90 degrees, it means that each angle must be smaller than 60 degrees. This is because if one angle were 90 degrees or more, the sum of the angles would be greater than 180 degrees, which is impossible.

So, there you have it. An acute triangle can have only acute angles because the sum of its interior angles must be 180 degrees. It’s a mathematical dance where the angles gracefully complement each other, keeping the triangle’s balance intact.