A Comprehensive Guide To Understanding Absolute Value: Notation, Properties, And Applications

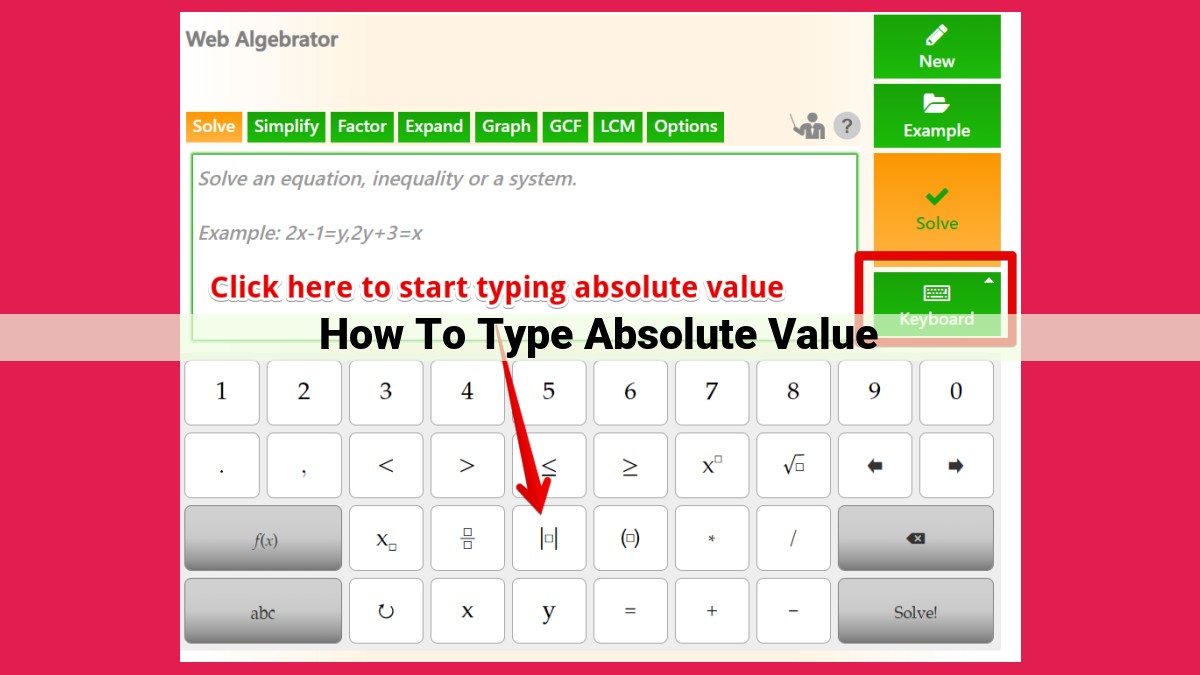
To type absolute value, use vertical bars (|) to enclose the expression. For instance, |5| represents the absolute value of 5. Alternatively, you can use |x|, where x is the value, indicating the distance from zero. Absolute value is always positive, representing the distance from zero on the number line. For example, |-5| = 5, as the distance from -5 to zero is 5 units. Absolute value finds applications in real-world situations like calculating distances and simplifying mathematical operations.

Vertical Bars: The Standard Absolute Value Notation

In the world of mathematics, absolute value is a concept that measures the distance from zero on the number line. And when it comes to representing absolute value, the standard notation involves two vertical bars (|) that embrace the expression being measured.

For instance, if we want to find the absolute value of -5, we write it as |-5|. These vertical bars tell us that we are looking at the distance from zero to -5 on the number line. Since -5 is five units away from zero, the absolute value of -5 is 5: |-5| = 5.

The vertical bar notation is a clear and concise way to represent absolute value. It helps us to distinguish between positive and negative numbers, and it ensures that the result is always positive.

Alternative Notation: |x|

Beyond the familiar vertical bars (| |) notation, there exists an alternative way to represent the absolute value: |x|. This simplified notation expresses the distance from zero on the number line, offering a convenient and concise way to denote absolute values.

Let’s delve into how this alternative notation works. Consider the expression |x|. In this notation, the vertical bars have been replaced by an absolute value symbol, which resembles an inverted “V” shape. The symbol encloses the variable x within it.

For example, the absolute value of -5 can be written as |-5|. This expression indicates the distance from zero to -5 on the number line. Since -5 is five units away from zero, |-5| = 5.

The absolute value of any number, whether positive or negative, is always positive. This property ensures that the result of an absolute value calculation conveys the magnitude of the number without considering its sign.

Tip for Easy Recall:

Remember the absolute value notation |x| as a special symbol that tells us to find the distance of x from zero. It’s like a special command that transforms any number, positive or negative, into its positive counterpart.

Unraveling the Enigma of Absolute Value

In the realm of mathematics, the concept of absolute value emerges as a fundamental pillar, shaping our understanding of distance and the behavior of numbers. But what exactly is absolute value, and how does it operate? Let’s embark on an illuminating journey to demystify this mathematical construct.

Defining Absolute Value: A Journey from Negativity to Positivity

Imagine a number line stretching infinitely in both directions. Absolute value is the notion of measuring the distance of a number from zero on this line. No matter which direction the number lies, the absolute value always yields a positive result.

The Sign Dilemma: Negatives Turn Positive

In the context of absolute value, the distinction between positive and negative numbers dissolves. Why? Because the sole purpose of absolute value is to capture the magnitude or distance from zero, regardless of whether the number is positive or negative.

Unveiling the Mathematical Shorthand

Mathematicians have devised a convenient notation to symbolize absolute value: vertical bars (| |) enclose the expression being measured. For instance, |5| represents the absolute value of 5, which is simply 5. Similarly, |-3| denotes the absolute value of -3, which is also 3. In essence, absolute value wipes away the negativity, leaving us with the number’s sheer magnitude.

Simplifying Operations with Absolute Value’s Assistance

Absolute value plays a crucial role in simplifying mathematical operations. Imagine you’re working with expressions like |2x – 5|. Without absolute value, the result could fluctuate between positive and negative values depending on the value of x. However, absolute value ensures that the result is always positive, making calculations more manageable and interpretable.

Absolute Value’s Applications in Our World

Beyond the realm of abstract mathematics, absolute value finds practical uses in our everyday lives. For instance, it helps us calculate distances, regardless of whether they involve positive or negative displacements. In physics, it aids in understanding the speed and direction of objects. Absolute value is a versatile tool that helps us navigate the complexities of our physical world.

Example: Finding the Absolute Value of a Negative Number

• Provide a step-by-step example of finding the absolute value of a negative number.
• Explain how to determine the distance from zero to the given number.

Unveiling the Absolute Truth: What’s the Deal with Absolute Value?

In the realm of mathematics, the concept of absolute value holds a special place. It’s like a superhero that helps us conquer the world of negative numbers and turn them into something manageable.

Vertical Bars: The Mighty Ruler of Absolute Value

Imagine an invisible wall called the number line. Numbers line up on this wall, some positive and some negative. The absolute value of a number tells us how far that number is from the zero mark. We use vertical bars (|) like mighty rulers to enclose the number we want to measure.

For example, if we have the number -5, we write its absolute value as |5|. The vertical bars tell us to ignore the negative sign and focus on the number’s distance from zero on the number line.

Alternative Notation: The Nifty Shortcut

There’s a handy shortcut we can use to denote absolute value: the simple |x| notation. The letter ‘x’ represents the number we’re measuring. So, |x| means the absolute value of x.

Grasping the Essence of Absolute Value

Absolute value is not just about finding distances. It’s the superhero that transforms negative numbers into positive ones. No matter what negative number we encounter, its absolute value will always be positive.

Example: Taming a Negative Number

Let’s conquer a negative number together. Suppose we have -7. To find its absolute value, we simply ignore the minus sign and focus on the number 7. So, |7| = 7. The absolute value of -7 is 7, the distance from zero to 7 on the number line.

Absolute Value’s Magical Powers in Real Life

Absolute value isn’t just a classroom concept. It has superpowers in the real world. From calculating distances to finding coordinates, absolute value helps us navigate our surroundings and make sense of mathematical operations.

Remember, absolute value is your guide in the world of positive and negative numbers. It’s like a brave knight that faces the challenges of negative numbers head-on and always brings back the positive side of things.

Absolute Value in the Real World: Unraveling Distance and Simplifying Calculations

The concept of absolute value extends beyond mathematical equations. In everyday life, it plays a crucial role in understanding distance and simplifying calculations.

Calculating Distances

Absolute value is the distance from zero on the number line. When you calculate the distance between two points, the negative signs don’t matter. You focus on the actual length between them. That’s where absolute value comes in. For example, if you’re driving 5 miles south and then 3 miles north, the total distance traveled is 5 + 3 = 8 miles. This is true even though you were driving in different directions. The absolute value of -5 is 5, and the absolute value of 3 is 3. So the total distance traveled is 5 + 3 = 8.

Simplifying Equations

Absolute value can also simplify mathematical operations. Take the equation:

y = x - 5

If x is less than 5, the result of x – 5 will be negative. To avoid dealing with negative numbers in calculations, we can use absolute value to eliminate the minus sign:

y = |x - 5|

Now, regardless of whether x is positive or negative, the result of |x – 5| will always be positive. This makes it easier to work with the equation.

In conclusion, absolute value is a powerful tool in the real world. It helps us calculate distances accurately, simplifies mathematical operations, and makes equations more manageable. Understanding absolute value is essential for tackling a wide range of problems, from navigation to everyday calculations.