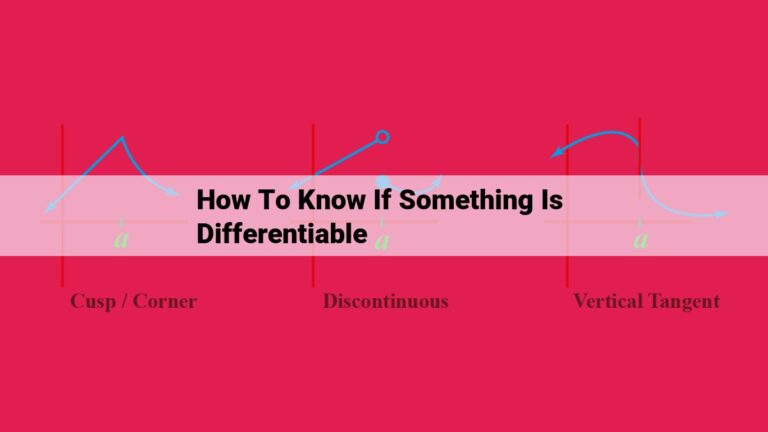
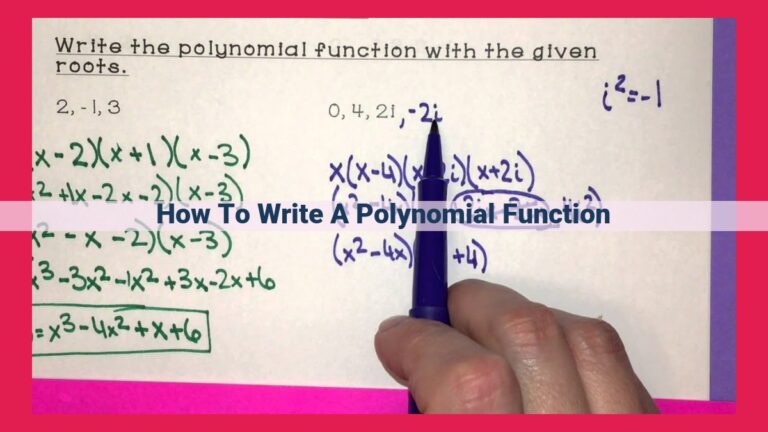
Uncover The Roots Of Polynomials: A Comprehensive Guide To Key Concepts And Solution Techniques

To find roots of a polynomial, begin by understanding its key concepts, including its definition and the Fundamental Theorem of Algebra. Leverage tools like the Rational Root and Descartes’ Rule of Signs theorems to identify potential roots. Utilize methods such as Newton’s Method for iterative refinement, Bisection Method for interval narrowing, or Secant and Regula Falsi methods for approximating roots. For complex roots, consider Bairstow’s Method. These techniques provide various approaches to accurately determine the roots of a polynomial.

Understanding Roots of a Polynomial: A Journey into the Heart of Equations

Prologue: The Quest for Roots

Imagine a polynomial equation as a riddle, where the roots are the hidden secrets waiting to be unveiled. Every polynomial, like an enigmatic fortress, guards its roots, and it’s our task as explorers to conquer them, to uncover the very essence of the equation.

I. Roots: The Gatekeepers of a Polynomial’s Output

A root is a special value for which a polynomial evaluates to zero. It’s like a key that unlocks the door to the polynomial’s behavior. When you plug this magical number into the equation, the result vanishes, leaving behind a trail of zeros like breadcrumbs leading you to the polynomial’s deepest secrets.

II. The Fundamental Theorem of Algebra: A Guiding Star

This theorem proclaims that every polynomial of degree n possesses exactly n roots, both real and complex. It’s like a compass for our journey, assuring us that the roots are there, waiting to be discovered, like hidden treasures beneath the sea.

III. Rational Root Theorem: A Bridge to Simplicity

If the coefficients of a polynomial are rational numbers (fractions), the rational root theorem offers a shortcut. It narrows down the search for potential roots to a finite list of possible candidates, like a lighthouse illuminating the path to our destination.

IV. Descartes’ Rule of Signs: A Clue from Coefficients

This rule provides a glimpse into the number of positive and negative real roots based on the signs of the polynomial’s coefficients. It’s like a spyglass that gives us a peek into the polynomial’s hidden structure, revealing the possible combinations of positive and negative roots.

Understanding the Roots of a Polynomial: The Fundamental Theorem of Algebra

In the realm of polynomial equations, finding roots is a crucial task, whether it’s for solving algebraic problems or understanding mathematical models. The Fundamental Theorem of Algebra serves as the cornerstone for our understanding of polynomial roots.

Imagine a polynomial equation like a complex puzzle. The roots, like hidden pieces, are the values of the variable that make the polynomial equal to zero. The Fundamental Theorem of Algebra states that for every polynomial with at least one non-zero coefficient, there exists at least one complex root.

This theorem opens up a Pandora’s box of implications. Firstly, it tells us that polynomials have at least one root, which means they can be completely factorized using these roots as factors. Secondly, it implies that there are as many distinct roots as the degree of the polynomial, providing a framework for finding all possible solutions.

The Fundamental Theorem of Algebra is a beacon of hope in the polynomial wilderness, assuring us that every equation holds at least one secret, waiting to be unlocked. It not only gives us confidence in finding roots but also guides us in approximating them, using methods like Newton’s Method or the Bisection Method.

So, next time you encounter a polynomial equation, remember the wise words of the Fundamental Theorem of Algebra. It may seem like an impenetrable fortress, but with perseverance and a touch of mathematical artistry, you can unearth its hidden truths and conquer the challenges it presents.

Unveiling the Rationality Behind Polynomial Roots: Unlocking the Potential

Rational Root Theorem: Unveiling the Hidden Symmetry

As we explore the enigmatic realm of polynomials, the Rational Root Theorem emerges as a guiding light, whispering secrets about the dwelling places of elusive roots. This profound theorem illuminates the path to identifying potential rational roots, those numbers that reside within the realm of fractions.

Imagine a polynomial as a majestic equation, its towering coefficients orchestrating a harmonious symphony of terms. The Rational Root Theorem empowers us to peer into this symphony and discern hidden rational notes – numbers that, when substituted into the polynomial, yield a comforting silence of zero.

The theorem’s mantra is as elegant as it is incisive: any rational root of a polynomial with integer coefficients must be a factor of the constant term divided by a factor of the leading coefficient. It’s like a secret code, empowering us to cast our discerning gaze upon the polynomial’s numerical framework and deduce potential candidates for roots.

Consider a polynomial with integer coefficients, its constant term c and leading coefficient a. The Rational Root Theorem whispers that any potential rational root p/q must conform to the following criteria:

• p is a factor of c
• q is a factor of a

The theorem unveils a tapestry of possible rational roots, narrowing down our search to a manageable realm. As we embark on the quest for roots, the Rational Root Theorem becomes an invaluable ally, guiding us towards promising candidates for further investigation.

Descartes’ Rule of Signs: Explain how to determine the possible number of positive and negative real roots based on coefficients.

Descartes’ Rule of Signs: Unveiling the Secrets of Polynomial Roots

In the captivating realm of polynomials, the enigmatic roots hold the key to unlocking their hidden mysteries. Enter Descartes’ Rule of Signs, a time-honored tool that guides us through the labyrinth of coefficients, revealing the possible number of positive and negative real roots concealed within.

Imagine a polynomial function, a mathematical expression that resembles a series of terms connected by addition or subtraction. Each term consists of a coefficient and a variable raised to a certain power. These coefficients, like the master puppeteers of the polynomial, hold the destiny of its roots in their sway.

Descartes’ Rule of Signs postulates that:

• The number of positive real roots is equal to the number of sign changes in the coefficients of the polynomial when written in decreasing order of terms.

• Conversely, the number of negative real roots is equal to the number of sign changes in the coefficients when written in increasing order of terms.

Consider the polynomial p(x) = x^3 – 2x^2 – 5x + 6. Its coefficients, starting from the highest degree term, are 1, -2, -5, and 6.

In decreasing order, the coefficients become: 1, -2, -5, 6. There is one sign change from negative to positive. Therefore, p(x) may have one positive real root.

In increasing order, the coefficients become: 6, -5, -2, 1. There is one sign change from positive to negative. Therefore, p(x) may have one negative real root.

Descartes’ Rule of Signs provides a quick and efficient method for estimating the number of real roots of a polynomial without actually solving for them. It serves as a compass, guiding us through the uncharted waters of polynomial exploration and helping us anticipate the treasures that lie ahead.

Understanding the Roots of a Polynomial: Newton’s Method

Newton’s Method: Unveiling Roots through Iteration

In our exploration of polynomial roots, we encounter the enigmatic Newton’s Method, an iterative technique that uses the derivative as a guiding force to progressively refine our root estimates.

Imagine a polynomial lurking in the shadows, its roots hidden from plain sight. Newton’s Method becomes our flashlight, illuminating the path to these elusive values. We start with an initial guess for the root, no matter how rough.

Armed with our guess, we calculate the polynomial’s derivative at that point. This derivative serves as a signpost, pointing us in the direction of the true root. We then take a small step in that direction and evaluate the polynomial again.

This dance between guessing, calculating, and updating repeats itself, each step bringing us closer to the hidden root. The derivative acts as our compass, guiding us towards the root’s lair.

As we continue this iterative journey, our guesses become increasingly precise, converging on the true root like a graceful ballet. The derivative becomes our trusted companion, leading us to the root’s doorstep.

The Heart of Newton’s Method

Newton’s Method revolves around a simple formula:

x_{n+1} = x_n - f(x_n) / f'(x_n)

Here, x_n+1 is our refined guess, x_n is our current guess, f(x) is the polynomial, and f'(x) is its derivative.

Each iteration of this formula chips away at the gap between our guess and the true root, until we reach a point where the difference is negligible. At this sweet spot, we have successfully unearthed the polynomial’s secret value.

Unlocking the Roots of a Polynomial: A Bisection Method Odyssey

In the quest for knowledge, we often encounter equations that hold hidden secrets within their depths. Polynomials, expressions composed of variables raised to various powers, are one such enigma. Their roots, the values that make them equal to zero, provide a crucial key to understanding their behavior.

One time-honored method for uncovering these roots is the bisection method. Picture yourself as an explorer, navigating a treacherous mountain range. Just as you would divide and conquer the peaks, the bisection method systematically splits the polynomial’s domain in half, searching for the root’s hiding place.

Consider the polynomial f(x). Our initial assumption is that the root lies within an interval [a, b] where f(a) < 0 and f(b) > 0. This ensures that at least one root exists between these bounds.

Next, we venture to the midpoint of the interval, c = (a + b)/2. By evaluating f(c), we gain valuable insight:

• If f(c) = 0, we have stumbled upon the root and our quest is over.
• If f(c) < 0, the root must lie in the lower half of the interval, so we update our interval to [a, c] and repeat the process.
• If f(c) > 0, the root must lie in the upper half of the interval, so we update our interval to [c, b] and continue our journey.

With determination and precision, we continue this bisection protocol, halving the interval with each iteration. As the boundaries tighten, our estimate of the root becomes more refined. Eventually, we reach a point where the interval is sufficiently small, providing us with the sought-after root.

The beauty of the bisection method lies in its simplicity and guaranteed convergence. No matter how complex the polynomial, it will lead us to a root, provided we start with an appropriate interval where a root is known to exist.

So, if you find yourself seeking the elusive roots of polynomials, embark on the bisection method adventure. With patience and persistence, you will conquer the unknown and uncover their deepest secrets.

Unveiling the Secrets of Roots: A Mathematical Odyssey

In the realm of mathematics, polynomials are enigmatic expressions that hold a profound secret: their roots. These special values unlock the mysteries of these algebraic equations, revealing essential information about their behavior and characteristics. Join us on an adventure to unravel the roots of a polynomial, uncovering the key concepts and powerful methods that illuminate this captivating subject.

Delving into the Definition of a Root

A root of a polynomial is an input value that, when plugged into the equation, produces an output of zero. It represents a point where the polynomial’s graph intersects the x-axis. Understanding the concept of a root is crucial for comprehending the behavior of polynomials and solving equations involving them.

The Significance of the Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra proclaims that every non-constant polynomial equation has at least one complex root. This fundamental truth underpins many techniques for finding roots, as it guarantees the existence of solutions, even if they may be complex numbers.

Rational Root Theorem: A Shortcut for Identifying Roots

Sometimes, it’s possible to identify potential rational roots of a polynomial using the Rational Root Theorem. This theorem provides criteria based on the coefficients of the polynomial to determine possible rational roots. If any of these potential roots satisfy the polynomial equation, they are guaranteed to be true roots.

Descartes’ Rule of Signs: Deciphering the Number of Roots

The Descartes’ Rule of Signs offers insights into the number of positive and negative real roots a polynomial may possess. By examining the sign changes in the polynomial’s coefficients, it’s possible to determine the maximum number of positive and negative real roots the equation can have.

Exploring Methods for Uncovering Roots

Now, let’s venture into the world of numerical methods, where we’ll explore powerful techniques for approximating the roots of polynomials. From _Newton’s Method to the _Bisection Method and beyond, each technique brings its own advantages and suits different scenarios.

Secant Method: Riding the Secant Line to Roots

The _Secant Method approximates roots by making educated guesses and iteratively refining them. It constructs a secant line between two points on the polynomial’s graph and uses its slope to predict the next guess. Unlike the Bisection Method, which relies on narrowing intervals, the Secant Method employs secant lines to converge more quickly towards the actual root.

Understanding the Roots of a Polynomial

Embarking on a mathematical journey, we delve into the world of polynomials, enigmatic expressions that hold secrets within their equations. Roots, the elusive values that make these polynomials vanish, are the keys to unlocking their mysteries.

Key Concepts

Definition of a Root: A root of a polynomial is a value that, when substituted into the polynomial, yields an output of zero. It’s like a magic number that makes the polynomial disappear!

Fundamental Theorem of Algebra: This profound statement asserts that every polynomial with real coefficients has at least one complex root. It’s as if the polynomial is destined to have a solution, no matter how complex.

Rational Root Theorem: This theorem provides a clever way to identify potential rational roots (fractions) of a polynomial. It’s a handy tool for narrowing down the search for roots.

Descartes’ Rule of Signs: This rule allows us to predict the number of positive and negative real roots based on the sign changes in the polynomial’s coefficients. It’s like a signpost that guides us towards the possible solutions.

Methods for Finding Roots

Newton’s Method: This iterative approach uses calculus to refine root estimates with each iteration. It’s like a Newton’s cradle, gracefully bouncing towards the solution.

Bisection Method: This method systematically divides the interval containing a root in half, narrowing the search with each iteration. It’s like a game of “guess and check,” gradually closing in on the target.

Secant Method: Similar to the bisection method, but instead of using interval halving, it uses secant lines to approximate roots. It’s like taking two points on the polynomial and drawing a line that intersects the x-axis at the approximate root.

Regula Falsi Method

The Regula Falsi Method, a clever blend of the bisection and secant methods, combines their strengths. It starts with an interval known to contain a root, then uses the secant method to estimate the root. But here’s the twist: instead of splitting the interval in half, it uses the false position to estimate the root. This false position is calculated as the point where the secant line intersects the x-axis. This method converges more rapidly than the bisection method, making it a powerful tool for finding polynomial roots.

In conclusion, understanding the roots of a polynomial is a fundamental skill in mathematics. By grasping the key concepts and employing the various root-finding methods, we can unlock the secrets hidden within these enigmatic equations and solve a wide range of mathematical problems.

Understanding Roots of a Polynomial: A Comprehensive Guide

In the realm of mathematics, polynomials hold a place of prominence. They are expressions characterized by their ability to represent various algebraic scenarios and functions. Finding the roots of a polynomial, also known as its zeros, is a fundamental aspect of working with these expressions.

Key Concepts: Roots and Theorems

A root of a polynomial is a value that, when plugged into the polynomial, results in an output of zero. The Fundamental Theorem of Algebra states that every polynomial with complex coefficients has at least one complex root. This principle provides a solid foundation for our exploration of roots.

The Rational Root Theorem offers a valuable tool for identifying potential rational roots of a polynomial. According to the theorem, all rational roots of a polynomial with integer coefficients must be expressible as the ratio of two integers, where the numerator is a factor of the constant term and the denominator is a factor of the leading coefficient.

Furthermore, Descartes’ Rule of Signs provides insights into the possible number of positive and negative real roots of a polynomial. By examining the signs of the coefficients, we can deduce the maximum number of roots of each type.

Methods for Finding Roots

Once we have a basic understanding of roots, we can embark on the task of finding them using a variety of methods. Newton’s Method utilizes the derivative of the polynomial to iteratively refine our estimates of the roots. This method is particularly effective when we have a good initial guess.

The Bisection Method, on the other hand, employs a divide-and-conquer strategy. It repeatedly bisects the interval containing the root, narrowing down the range with each iteration.

Secant Method is similar to the bisection method, but instead of using the midpoint, it uses a secant line to approximate the root. This method often converges faster than the bisection method.

Regula Falsi Method combines the bisection method and secant method, offering a robust approach for finding roots.

Bairstow’s Method: Unveiling Complex Roots

Bairstow’s Method emerges as a powerful tool for finding complex roots of polynomials. It employs synthetic division in a novel way to isolate the complex roots, often in pairs.

To delve into the intricate details of Bairstow’s Method, we recommend exploring dedicated resources and consulting with experts in the field.