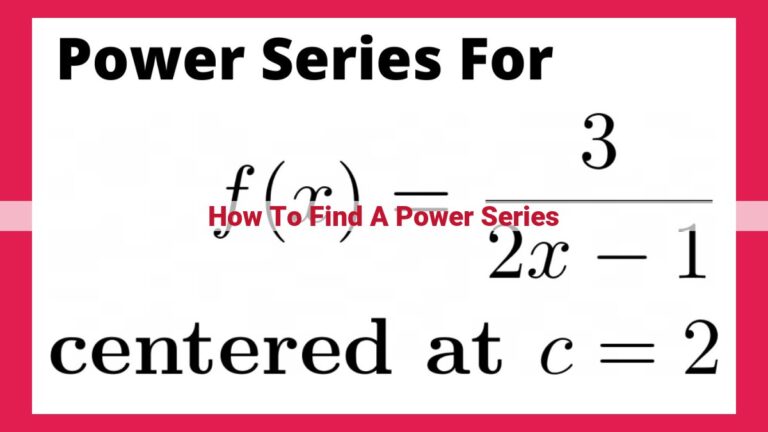Ultimate Guide To Series Convergence Tests For Seo-Boosting Optimization

To determine the convergence of a series, various tests can be employed: The Integral Test uses an integral to approximate the series sum; the Comparison Test compares it to known convergent/divergent series; the Limit Comparison Test analyzes the limit of a ratio for convergence; the Alternating Series Test checks for alternating terms and decreasing magnitude; the Ratio Test evaluates the limit of consecutive term ratios for absolute convergence; the Root Test examines the nth root of absolute term values; Cauchy’s Condensation Test simplifies series by preserving every kth term; and Dirichlet’s Test supplements the Alternating Series Test with additional conditions.

The Integral Test: A Powerful Tool for Determining Convergence

Imagine yourself embarking on a journey to determine the fate of an infinite series: whether it converges or diverges, like a traveler seeking the end of an unknown path. The Integral Test is your trusty guide, offering a systematic approach to unravel this mystery.

How it Works:

The Integral Test draws a parallel between a series and an integral. The key idea is that if the integral of the series’ terms is finite, the series converges. Conversely, if the integral diverges, the series also diverges.

Steps to Apply the Integral Test:

1. Integrate the series’ terms: Find the integral of the function that defines the terms of the series.
2. Evaluate the Integral: Determine the value of the integral.
3. Make the Decision: If the integral is finite (has a definite value), the series converges. If the integral diverges (does not have a definite value), the series diverges.

Example:

Consider the series:

Σ(n=1 to ∞) 1/n^2

Applying the Integral Test:

∫(1 to ∞) 1/x^2 dx = lim (x→∞) [-1/x] (1 to ∞)

The integral evaluates to -1, a definite value. Therefore, the series converges.

Benefits of the Integral Test:

• Simplicity: It involves straightforward integration, eliminating the need for complex calculations.
• Versatility: It can be applied to a wide range of series, including those with positive, negative, or oscillating terms.
• Provides Analytical Insight: By integrating the series’ terms, the Integral Test offers a deeper understanding of the series’ behavior.

The Comparison Test:

• How the Comparison Test works and when it can be used.
• Using a convergent or divergent series as a benchmark for comparison.

The Comparison Test: A Powerful Tool for Convergence and Divergence

When it comes to determining the convergence or divergence of infinite series, the Comparison Test emerges as a valuable tool in our mathematical arsenal. This test provides a straightforward approach to analyze series by comparing them to well-known convergent or divergent series.

The Comparison Test operates on the fundamental principle that if two series have similar behavior, then they share the same fate in terms of convergence or divergence. Specifically, if the terms of a series are smaller than the terms of a convergent series, the given series must also converge. Conversely, if the terms of a series are larger than the terms of a divergent series, the given series must also diverge.

To apply the Comparison Test effectively, we need to identify a series whose convergence or divergence is already known and whose terms are comparable to the terms of the given series. If we can show that the terms of the given series are consistently smaller or larger than the terms of the reference series, we can conclude the convergence or divergence of the given series accordingly.

For instance, let’s consider the series 1 + 1/2 + 1/4 + 1/8 + …. Since each term in the given series is smaller than the corresponding term in the convergent geometric series 1 + 1/2 + 1/4 + 1/8 + … (where the common ratio is 1/2), we can deduce that the given series converges by the Comparison Test.

In contrast, consider the series 1 – 1 + 1 – 1 + 1 – …. This series has alternating positive and negative terms. We can compare it to the divergent harmonic series 1 + 1/2 + 1/3 + 1/4 + …. Since each term in the given series has a larger absolute value than the corresponding term in the divergent harmonic series, we can conclude that the given series diverges by the Comparison Test.

The Comparison Test serves as a straightforward and versatile tool for determining the convergence or divergence of series. By comparing series to well-known convergent or divergent series, we can quickly and efficiently classify the behavior of infinite sums.

The Limit Comparison Test: A Powerful Tool for Series Convergence

When it comes to determining the convergence or divergence of an infinite series, the Limit Comparison Test shines as a valuable analytical tool. This test relies on a simple yet effective principle: comparing the given series with a known convergent or divergent series.

When to Use the Limit Comparison Test:

The Limit Comparison Test is applicable when the terms of the given series, denoted as an, are all positive or all negative. It requires the existence of another series, denoted as bn, where the terms are also all positive or all negative. The key condition for using the test is that the limit of the ratio of an/bn as n approaches infinity must exist and be a positive finite number, excluding zero.

Understanding the Test:

The Limit Comparison Test is based on the idea that if the limit of an/bn approaches a positive finite value, then the series Σan and Σbn either both converge or both diverge. In other words, the behavior of the known series, whether convergent or divergent, is “transferred” to the given series.

Steps for Applying the Test:

1. Identify a Suitable Comparison Series: Find a series bn that satisfies the positivity or negativity condition and has a known convergence or divergence status.
2. Calculate the Limit: Determine the limit of the ratio an/bn as n approaches infinity.
3. Draw Conclusions: Based on the limit’s value:
   • If the limit is positive and finite, both series either converge or diverge.
   • If the limit is zero, the test is inconclusive, and other tests may be required.
   • If the limit is negative or infinite, the test cannot be applied.

The Limit Comparison Test is a versatile tool that can be used to analyze a wide range of series. It provides a quick and reliable method for determining convergence or divergence when the terms of the series are difficult to evaluate directly.

The Alternating Series Test: A Guide to Convergence

In the realm of infinite series, the Alternating Series Test emerges as a powerful tool for determining the convergence of alternating series. This valuable test provides clear criteria to assess whether a series of alternating signs fluctuates sufficiently to approach a finite value.

The Alternating Series Test relies on two key requirements: the terms of the series must alternate in sign, from positive to negative (or vice versa), and the absolute values of the terms must form a decreasing sequence. These requirements ensure that the positive and negative terms of the series effectively cancel each other out, leading to an overall convergent behavior.

In practice, applying the Alternating Series Test to an alternating series involves the following steps:

1. Check the signs: Verify that the terms of the series are indeed alternating in sign, either positive-negative or negative-positive.
2. Examine the sequence: Determine whether the absolute values of the terms form a decreasing sequence. This means that each absolute value should be less than or equal to the absolute value of the previous term.
3. Conclude convergence: If both conditions are met, you can confidently conclude that the alternating series converges.

Example:

Consider the series $\sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n}$. This series alternates in sign and its absolute values, $\left| (-1)^{n+1} \frac{1}{n} \right| = \frac{1}{n}$, form a decreasing sequence. Therefore, by the Alternating Series Test, we can conclude that this series converges.

Dirichlet’s Test: A Refined Approach

While the Alternating Series Test provides a reliable indication of convergence, Dirichlet’s Test offers a more refined approach in certain cases. Dirichlet’s Test adds an extra condition: the limit of the absolute values of the terms must be zero.

This additional condition ensures that the terms eventually become insignificant, even as they alternate in sign. By combining the Alternating Series Test with Dirichlet’s Test, we obtain a more precise convergence analysis.

Example:

The series $\sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n^2}$ satisfies the Alternating Series Test but fails Dirichlet’s Test because $\lim_{n\to\infty} \frac{1}{n^2} \neq 0$. Consequently, this series diverges.

The Alternating Series Test and Dirichlet’s Test are invaluable tools in the toolkit of any mathematician or student seeking to understand the convergence of alternating series. By applying these tests, we can effectively determine whether a series converges or diverges, shedding light on the behavior of infinite sums.

The Ratio Test: A Powerful Convergence Tool for Infinite Series

In the realm of infinite series, the Ratio Test emerges as an indispensable tool for determining whether a series converges absolutely. This test relies on a simple yet profound principle: the behavior of the ratio of consecutive terms in a series can provide crucial insights into its ultimate convergence or divergence.

To understand the Ratio Test, let’s delve into its application. Given an infinite series ∑_(n=1)^∞ a_n, we calculate the limit of the ratio of consecutive terms as n approaches infinity:

lim_(n→∞) |a_(n+1)/a_n|

If this limit exists and is less than 1, the series ∑_(n=1)^∞ a_n converges absolutely. In other words, the series converges and its sum is finite. However, if the limit is greater than 1 or does not exist, the series diverges.

The Ratio Test is particularly useful when the terms of a series do not have a clear pattern or when other convergence tests, such as the Integral Test or Comparison Test, are inconclusive. By analyzing the ratio of terms, we can gain valuable information about the series’ behavior and determine its convergence or divergence.

For example, consider the series ∑_(n=1)^∞ (1/n^2). Applying the Ratio Test, we find:

lim_(n→∞) |(1/(n+1)^2)/(1/n^2)| = lim_(n→∞) (n/(n+1))^2 = 1

Since the limit is 1, which is less than 1, the series ∑_(n=1)^∞ (1/n^2) converges absolutely.

In conclusion, the Ratio Test is a powerful and versatile tool that allows us to determine the convergence of infinite series with relative ease. By examining the ratio of consecutive terms, we can uncover the underlying behavior of the series and establish whether it converges absolutely or diverges.

The Root Test:

• When the Root Test is applicable.
• Evaluating the nth root of the absolute value of terms to determine convergence or divergence.

The Root Test: A Powerful Tool for Convergence Analysis

In the realm of mathematics, determining whether an infinite series converges or diverges is a fundamental challenge. Among the many tools available for this task, the Root Test stands out as a particularly effective method.

When to Apply the Root Test

The Root Test is applicable to series with positive terms, which means each term in the series is greater than zero. If the series contains negative terms or a mixture of positive and negative terms, alternative tests, such as the Alternating Series Test, must be used.

The Test Procedure

The Root Test involves evaluating the nth root of the absolute value of the nth term of the series. The test proceeds as follows:

1. Calculate the limit of the nth root of the absolute value of the nth term as n approaches infinity.
2. If the limit is less than 1, the series converges.
3. If the limit is equal to 1, the test is inconclusive, and alternative tests must be used.
4. If the limit is greater than 1, the series diverges.

Intuition Behind the Test

The Root Test exploits the concept of geometric series. If the nth root of the nth term converges to a value less than 1, the terms in the series are shrinking relatively faster than a geometric series with a common ratio less than 1, which is known to converge. Conversely, if the limit is greater than 1, the terms are growing relatively faster than a divergent geometric series with a common ratio greater than 1.

Example

Consider the series:

1 + 1/2 + 1/4 + 1/8 + ... + 1/2^n + ...

Using the Root Test:

lim(n->∞) (1/2^(1/n)) = lim(n->∞) 1/2 = 1/2 < 1

Since the limit is less than 1, the series converges.

Cauchy’s Condensation Test: Simplifying Series for Convergence Analysis

In the vast world of mathematics, there are numerous tools that help us determine whether an infinite series converges or diverges, and one such tool is Cauchy’s Condensation Test. This test provides a simplified approach to analyze series for convergence, making it a valuable asset in our mathematical toolbox.

The Essence of Cauchy’s Condensation Test

Cauchy’s Condensation Test condenses an infinite series by keeping every kth term, where k is a positive integer. This condensed series, denoted as S_k, is then compared to the original series S to determine its convergence or divergence.

Condensation Process

Suppose we have an infinite series S given by S = a_1 + a_2 + a_3 + …. + a_n + ….

To condense this series using Cauchy’s test, we take every kth term and form a new series S_k:

S_k = a_k + a_2k + a_3k + …. + a_nk + ….

The value of k represents the “condensation factor,” where higher values of k result in a more condensed series.

Convergence Determination

The key to using Cauchy’s Condensation Test is to compare the convergence of the original series S to the convergence of the condensed series S_k.

• Convergence: If the condensed series S_k converges to a finite limit, then the original series S also converges.
• Divergence: However, if the condensed series S_k diverges to infinity or oscillates without converging, then the original series S also diverges.

Intuitive Explanation

Cauchy’s Condensation Test simplifies the analysis of series by condensing them into a more manageable form. The condensed series S_k contains the most dominant terms of the original series, as smaller terms are grouped together and their contributions become negligible. Therefore, if S_k converges, it indicates that the dominant terms gradually approach a finite limit, and the original series is likely to behave similarly. Conversely, if S_k diverges, it means that the dominant terms continue to grow without bound, indicating divergence in the original series as well.

Practical Application

Cauchy’s Condensation Test finds practical use in analyzing series that contain a mix of positive and negative terms. By condensing the series, we eliminate the oscillations caused by opposite-sign terms and focus on the overall convergence behavior of the dominant terms. This makes it easier to determine whether the series converges absolutely, conditionally, or diverges altogether.

Dirichlet’s Test (for Alternating Series):

• An alternative approach to the Alternating Series Test.
• Examining the limits of positive and negative terms to determine convergence.

Dirichlet’s Test: An Alternative Approach to Alternating Series

When it comes to determining the convergence or divergence of alternating series (series with alternating positive and negative terms), the Alternating Series Test is a common tool. However, there’s an alternative approach known as Dirichlet’s Test that provides additional insights.

Dirichlet’s Test focuses on examining the limits of the positive and negative terms of the series. If the limits both exist and are nonzero, the series converges. In other words, the series will converge if the alternating terms approach a fixed nonzero value.

How to Apply Dirichlet’s Test:

1. Check the Alternating Pattern: Confirm that the series alternates between positive and negative terms.
2. Identify Positive and Negative Terms: Isolate the positive and negative terms of the series. Let’s call them (a_n) and (-b_n), respectively.
3. Evaluate the Limits: Determine the limits of (a_n) and (-b_n) as (n) approaches infinity.
4. Apply the Test: If both limits exist and are nonzero, the series converges. Otherwise, the series diverges.

Example:

Consider the alternating series (1 – \frac{1}{2} + \frac{1}{3} – \frac{1}{4} + \cdots).

• The positive terms are (a_n = 1, \frac{1}{3}, \frac{1}{5}, \cdots), which approach 0 as (n) gets large.
• The negative terms are (-b_n = \frac{1}{2}, \frac{1}{4}, \frac{1}{6}, \cdots), which also approach 0.

Since both limits exist and are nonzero (although equal to 0), Dirichlet’s Test confirms that the series converges.