Ultimate Guide To Calculating Cosine From Sine Using The Pythagorean Identity
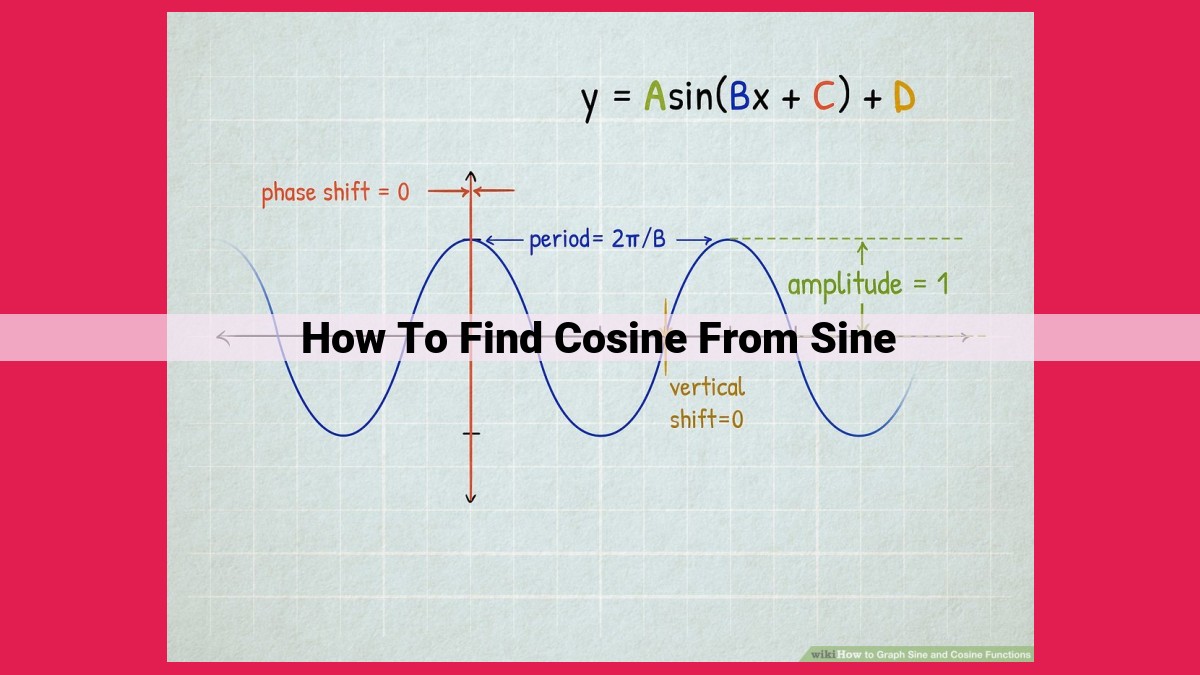
To find cosine (cos) from sine (sin), use the Pythagorean identity: cos²θ + sin²θ = 1. Square the given sin value and subtract it from 1 to obtain cos². Take the square root of cos² to get the absolute value of cos. Determine the sign of cos based on the angle’s quadrant to obtain the final cosine value. For example, if sin(30°) = 1/2, then cos²(30°) = 1 – (1/2)² = 3/4, so cos(30°) = ±√(3/4) = ±0.866.
- Define inverse trigonometric functions and their uses.
- Introduce sine and cosine as fundamental trigonometry concepts.
Navigating the Labyrinth of Inverse Trigonometric Functions, Sine, and Cosine
Embarking on a mathematical journey, we delve into the realm of inverse trigonometric functions, a set of functions that undo the work of their trigonometric counterparts, allowing us to extract angles from their trigonometric values. Among this family, the arcsine function stands out as the inverse of the beloved sine function, a fundamental concept in trigonometry.
Understanding the Sine Function
Picture a circle of radius 1, known as the unit circle. The sine function assigns a value between -1 and 1 to each angle on this circle, based on the vertical coordinate of the point where an imaginary ray from the circle’s center intersects the circle. This vertical coordinate is the sine value of the angle.
Cosine as a Companion to Sine
The cosine function, in harmony with the sine function, measures the horizontal coordinate of the same point on the unit circle. Its graph mirrors that of the sine function, shifted by a quarter turn to the left.
Finding Cosine from Sine
To find the cosine of an angle given its sine, we invoke the Pythagorean identity: sin² θ + cos² θ = 1. This identity enables us to calculate the cosine using the formula: cos θ = ±√(1 - sin² θ). The sign of the cosine depends on the quadrant in which the angle lies.
Applications of Cosine
Cosine extends far beyond theory, finding practical applications in various fields. In triangle trigonometry, it plays a pivotal role in cosine law, used to determine the length of a side of a triangle based on the other two sides and the angle opposite the unknown side. In navigation, cosine helps calculate distances and directions based on latitude and longitude coordinates.
Inverse Trigonometric Functions
- Explain the arcsine function and its relationship to sine.
- Discuss applications in calculus and advanced mathematics.
Inverse Trigonometric Functions: Arcsine and Its Applications
In the realm of mathematics, we often encounter functions that are defined as the inverse of other functions. Inverse trigonometric functions, like the arcsine, are no exception. These functions play a crucial role in calculus and advanced mathematics, offering insights into the relationship between angles and trigonometric ratios.
Understanding the Arcsine Function
The arcsine function, denoted as arcsin(x), is defined as the inverse function of sine. In essence, it determines the angle that produces a given sine value. For instance, arcsin(0.5) returns the angle 30 degrees, as sine(30°) = 0.5.
Relationship to the Sine Function
The arcsine function is intimately related to the sine function. The inverse relationship between them means that if y = arcsin(x), then sin(y) = x. This relationship is essential for understanding the behavior of the arcsine function.
Applications in Calculus
In calculus, the arcsine function finds its place when dealing with integrals of the form ∫(1/√(1-x²)) dx. By utilizing the substitution u = sinθ and applying the arcsine function, the integral can be simplified and evaluated.
Advanced Mathematical Applications
Beyond calculus, the arcsine function has applications in various branches of mathematics, including complex analysis, differential geometry, and number theory. It provides a foundation for understanding topics such as conformal mappings, special functions, and elliptic curves.
The arcsine function, as an inverse trigonometric function, stands as a powerful tool in both calculus and advanced mathematics. Its relationship to the sine function and its ability to determine angles from trigonometric ratios make it an indispensable tool for mathematical exploration and problem-solving.
Understanding the Sine Function
- Define the sine function and plot its graph.
- Explain the unit circle interpretation of sine values.
- Connect sine to the Pythagorean theorem.
Understanding the Sine Function: A Journey into the Essence of Trigonometry
In the realm of trigonometry, the sine function emerges as a fundamental concept, gracing us with its presence in a myriad of applications. To comprehend its enigmatic nature, let us delve into its definition and explore the tapestry of insights it unveils.
The sine function, denoted as sin(x), is the ratio of the opposite side to the hypotenuse in a right triangle. As the angle x increases from 0 to 360 degrees, the sine value oscillates between -1 and 1, creating a characteristic sinusoidal graph. This graph resembles a gentle wave, reflecting the periodic nature of the function.
The Unit Circle: A Window into Sine’s Symphony
To unravel the secrets of the sine function, we turn to the unit circle. This hallowed geometrical construct, with a radius of one unit, becomes a stage upon which the sine function performs its captivating dance. As an angle x rotates counterclockwise around the circle, the sine value is represented by the y-coordinate of the point where the terminal side of the angle intersects the circle. This ingenious graphical representation illuminates the connection between the angle measure and the corresponding sine value.
Sine and the Pythagorean Theorem: An Intimate Connection
The sine function is inextricably intertwined with the Pythagorean theorem, a cornerstone of Euclidean geometry. This hallowed equation, a² + b² = c², dictates the relationship between the sides of a right triangle. By leveraging this theorem, we can establish a profound bond between sine and the other trigonometric functions. For instance, the cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse, and the Pythagorean theorem reveals that sin²x + cos²x = 1. This identity underscores the complementary nature of sine and cosine, two functions that gracefully complement each other in the trigonometric realm.
By unraveling the depths of the sine function, we gain a profound understanding of its role in trigonometry. From its graphical representation to its connection with the Pythagorean theorem, the sine function unveils a world of mathematical beauty and practical applications. Its mastery unlocks a gateway to the fascinating world of trigonometry, where angles and triangles dance harmoniously.
Cosine Function: The Faithful Companion of Sine
In the realm of trigonometry, the sine function reigns supreme, measuring the vertical displacement of an angle. But its loyal companion, the cosine, plays an equally vital role. Defined as the ratio of the adjacent side to the hypotenuse in a right triangle, the cosine function is the embodiment of horizontal displacement.
Its graph, a gentle cosine wave, mirrors that of its sinusoidal counterpart, rising and falling with equal grace. This complementary relationship becomes even more apparent when we venture into the world of wave theory. Just as sine waves describe up-and-down oscillations, cosine waves depict side-to-side vibrations. This makes cosine invaluable in fields like acoustics and quantum mechanics, where it describes the propagation of sound waves and the movement of subatomic particles.
But cosine’s versatility extends far beyond wave theory. In harmonic motion, a motion that repeats itself periodically, cosine functions are used to model the displacement of objects vibrating with a constant frequency. From the rhythmic swing of a pendulum to the harmonious oscillation of a guitar string, cosine provides a mathematical framework for understanding these cyclical phenomena.
In short, the cosine function is an indispensable tool for understanding the world around us. While sine measures verticality, cosine complements it with horizontality. Together, they form a harmonious duo that orchestrates a symphony of physical and mathematical insights.
Unveiling Cosine: A Journey from Sine
In the intricate world of trigonometry, where angles and triangles dance, the inverse trigonometric functions, sine, and cosine play pivotal roles. While we’ve explored the enigmatic arcsine and delved into the sine’s profound applications, the time has come to delve into the fascinating depths of cosine and uncover its intimate connection to sine.
Finding cosine from sine is a captivating quest that reveals the harmonious interplay between these two trigonometric functions. Embark on this journey with us as we guide you through the magical steps, unveil the secrets of quadrant-based signs, and showcase captivating examples that illuminate cosine’s practical applications.
Step 1: Illuminating the Pythagorean Identity
The Pythagorean identity, a timeless equation that connects the sine and cosine of an angle, serves as our guiding light in this endeavor. It whispers, “sine squared plus cosine squared equals 1.” This precious formula empowers us to effortlessly find cosine when sine is known.
Step 2: Deciphering Quadrant Signs
Cosine’s sign, like a chameleon, changes its guise based on the angle’s quadrantal residence. In the majestic first quadrant, where both sine and cosine reside in positivity, cosine proudly wears the plus sign. In the enigmatic second quadrant, where sine reigns supreme but cosine ventures into negativity, the minus sign becomes its cloak. In the shadowy third quadrant, where both functions reside in negative territory, cosine embraces the plus sign once more. And finally, in the enigmatic fourth quadrant, where cosine reigns but sine hides in the negative realm, the minus sign becomes its steadfast companion.
Step 3: Illuminating Examples
To solidify our understanding, let’s embark on a journey of examples. Suppose we have an angle with a sine of 0.5. Plugging this value into the Pythagorean identity, we have:
0.5² + cosine² = 1
Solving for cosine, we discover its value to be 0.866. However, wait! We must remember the quadrantal sign convention. Since our example lies in the first quadrant, cosine gleefully adorns the plus sign, giving us a final answer of +0.866.
In another realm, consider an angle with a sine of -0.75. Following the same ritual, we conjure the Pythagorean identity:
(-0.75)² + cosine² = 1
Unveiling cosine, we find its value to be 0.625. But hold! The angle resides in the enigmatic third quadrant, where cosine enjoys the company of the plus sign. Thus, our final answer gracefully emerges as +0.625.
The journey to find cosine from sine has been a captivating exploration of trigonometric connections. Through the lens of the Pythagorean identity and the wisdom of quadrantal signs, we’ve unlocked the secrets of this intertwined realm. Remember, the sine and cosine stand as inseparable allies, their bond forged in the depths of trigonometric principles. Their practical applications, from triangle trigonometry to navigation and beyond, attest to their indispensable roles in our quest to unravel the mysteries of the mathematical universe. May this journey inspire you to continue exploring the enchanting tapestry of trigonometry, where every step unveils new insights and strengthens our understanding of the world around us.
Applications of Cosine: A Versatile Function in Trigonometry, Navigation, and Beyond
Beyond its fundamental role in trigonometry, the cosine function finds widespread applications in diverse fields, extending its reach far beyond the confines of mathematical equations.
Triangle Trigonometry and the Cosine Law:
In triangle trigonometry, the cosine law provides a powerful tool for solving triangles when only two sides and an included angle are known. This law relates the length of the third side to the other two sides and the cosine of the included angle. This knowledge is invaluable in various fields, including surveying, engineering, and architecture, where precise measurements and calculations are essential.
Navigation and Finding Direction:
In navigation, the cosine function plays a crucial role in calculating distances and directions traveled. By utilizing the cosine law in conjunction with other trigonometric relationships, navigators can accurately determine their position and course. This ability has been instrumental in the development of maritime navigation and the exploration of vast oceans.
Engineering and Physics: Harmonic Motion and Wave Propagation:
In engineering and physics, the cosine function finds applications in describing harmonic motion and wave propagation. Harmonic motion, characterized by sinusoidal oscillations, is prevalent in mechanical systems, such as springs and pendulums. Understanding cosine helps engineers design and analyze these systems for optimal performance. Similarly, in wave propagation, such as sound and light waves, the cosine function describes the displacement of particles, allowing scientists to study wave characteristics and behaviors.
In conclusion, the cosine function extends its influence beyond the realm of trigonometry into practical applications that shape our world. From calculating distances in navigation to describing motion in engineering, the cosine function remains an indispensable tool, demonstrating the interconnectedness of mathematics and the real world. By embracing its versatility, we unlock the potential for innovation and advancement in science, technology, and everyday life.