Master Trigonometry: A Comprehensive Guide To Angles, Ratios, And Triangle Measurement

To find angles in trigonometry, understand the angles of elevation and depression, which are used to measure angles from a horizontal line. Use the Pythagorean theorem to calculate these angles. Explore sine, cosine, and tangent trigonometric ratios and utilize special right triangles to simplify their calculation. Finally, find angles using trigonometry by identifying the relevant trigonometric ratio and solving for the unknown angle.

Exploring the World of Angles: Elevating and Depressing Perspectives

In the realm of mathematics, angles play a crucial role in describing the relationship between lines and planes. Among these angles, those of elevation and depression hold particular significance.

Elevation angles measure the upward slope of a line of sight from an observer to an object, while depression angles measure the downward slope. These angles find wide application in fields such as surveying, navigation, and astronomy.

To grasp the concept of these angles, consider the scenario of an observer on the ground looking up at a tall building. The observer’s line of sight forms an angle with the horizontal, known as the angle of elevation. Similarly, if the observer were looking down at a sunken object in a lake, the angle formed would be the angle of depression.

Understanding these angles is essential for determining the height or depth of objects relative to the observer’s position. By employing the Pythagorean theorem, it becomes possible to calculate these angles precisely, paving the way for further trigonometric explorations.

Understanding Angles of Elevation and Depression

Have you ever looked up at a tall building or down at the bottom of a well and wondered how to measure their heights or depths? The answer lies in the fascinating world of trigonometry.

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. In this context, two special angles are crucial: the angle of elevation and the angle of depression.

Angle of Elevation

Imagine standing on the ground and looking up at a flagpole. The angle formed between the horizontal and the line of sight to the top of the flagpole is called the angle of elevation. It tells you how high the object is relative to your eye level.

Angle of Depression

Conversely, if you’re on a bridge and looking down at a boat in the water, the angle formed between the horizontal and the line of sight to the boat is known as the angle of depression. It represents the depth of the object below your eye level.

Using the Pythagorean Theorem

Determining the angles of elevation and depression is essential for measuring heights and depths. One technique involves using the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.

Consider a right triangle where the hypotenuse is the line of sight (s) and the other two sides are the horizontal distance (a) and the vertical height (h). The Pythagorean theorem can be expressed as:

s² = a² + h²

This equation can be rearranged to find h:

h = √(s² - a²)

By knowing the line of sight and the horizontal distance, we can determine the vertical height using the Pythagorean theorem.

Dive into the Realm of Trigonometry: A Beginner’s Guide

Embark on a captivating journey into the world of trigonometry, the language of angles and triangles that unlocks a treasure trove of mathematical secrets. Let’s unravel its foundational elements and discover how they empower us to tackle real-world challenges.

Understanding Sine, Cosine, and Tangent: The Power Trio

At the heart of trigonometry lie three enigmatic functions: sine (sin), cosine (cos), and tangent (tan). These trigonometric ratios paint a vivid picture of a right triangle, providing a roadmap to unlock its mysteries.

Sine reveals the ratio of the length of a triangle’s opposite side to the length of its hypotenuse (the side opposite the right angle). It measures the vertical displacement relative to the hypotenuse.

Cosine, on the other hand, reveals the ratio of the length of the adjacent side (the side adjacent to the desired angle) to the length of the hypotenuse. It measures the horizontal displacement relative to the hypotenuse.

Tangent takes a different approach, showcasing the ratio of the length of the opposite side to the length of the adjacent side. It embodies the slope of the line formed by the opposite and adjacent sides, providing a measure of the slant or angle of inclination.

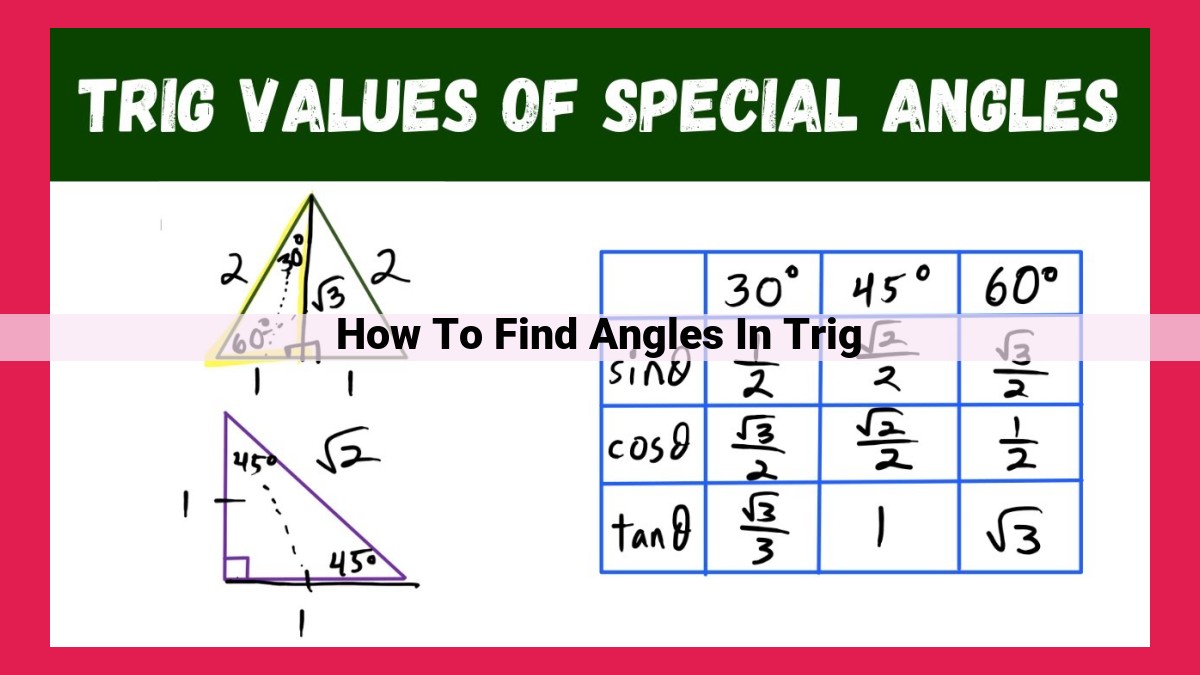
To grasp these concepts, it’s crucial to explore the special right triangles—the 30-60-90 triangle and the 45-45-90 triangle—which serve as invaluable tools for finding trigonometric ratios without delving into complex calculations.

Trigonometry Simplified: A Step-by-Step Guide to Finding Angles

Imagine yourself standing at the foot of a towering building, gazing up at its magnificent height. How do you determine its elevation, or the angle at which it rises above the ground? Enter the world of trigonometry, where angles are our guiding light.

Sine, Cosine, and Tangent: The Master Trio

In trigonometry, we have three fundamental trigonometric ratios: sine, cosine, and tangent. These ratios are the keys to unlocking the secrets of angles. Let’s dive into each one:

• Sine (sin): Remember that soaring skyscraper? The sine of an angle is the ratio of the opposite side (the height of the building) to the hypotenuse (the length from you to the top of the building).

• Cosine (cos): Shifting our focus to the ground, the cosine of an angle is the ratio of the adjacent side (the distance from you to the building) to the hypotenuse.

• Tangent (tan): Finally, the tangent of an angle is the ratio of the opposite side to the adjacent side. In our building example, the tangent would tell us the ratio of the building’s height to our distance from it.

Special Right Triangles: Our Trigonometry Buddies

To make angle-finding even more manageable, we rely on special right triangles. These triangles have familiar angle measures, such as 30-60-90 or 45-45-90 degrees. By studying these triangles, we can easily derive key trigonometric ratios:

• 30-60-90 Triangle: In this triangle, the sine of 30 degrees is 1/2, the cosine of 30 degrees is √3/2, and the tangent of 30 degrees is 1/√3.

• 45-45-90 Triangle: Here, the sine of 45 degrees is √2/2, the cosine of 45 degrees is √2/2, and the tangent of 45 degrees is 1.

Next up, we’ll guide you through finding angles using these trigonometric ratios. Stay tuned for our next blog post in this series!

Unlocking the Secrets of Angles: A Journey into Trigonometry

Embark on an intriguing adventure into the realm of trigonometry, where we’ll explore the captivating world of angles, sine, cosine, and tangent.

Understanding Angles of Elevation and Depression

Imagine yourself standing at the base of a towering skyscraper, gazing up at its dizzying heights. The angle you form with the horizontal line is known as the angle of elevation. Conversely, if you’re perched atop the building and looking down, you’re measuring the angle of depression. These angles play a crucial role in everyday life, from surveying land to guiding ships at sea.

Exploring Sine, Cosine, and Tangent

Trigonometry’s heart lies in understanding three essential trigonometric ratios: sine, cosine, and tangent. These ratios reveal the relationship between the sides of a right triangle and the angles formed. Special right triangles, like the 30-60-90 and 45-45-90 triangles, hold the key to effortlessly finding these ratios.

Finding Angles Using Trigonometry: A Step-by-Step Journey

Now, let’s embark on a step-by-step quest to decode angles using trigonometry. First, we’ll identify the relevant trigonometric ratio based on the known sides of the triangle. Then, we’ll employ inverse trigonometric functions to unveil the mysterious angle. These functions act as the mathematical Rosetta Stone, translating trigonometric ratios back into angles.

Step by step, we’ll navigate the labyrinth of angles, unraveling the hidden stories they hold. Along the way, we’ll encounter practical applications in fields like navigation, surveying, and architecture. Join us on this trigonometric odyssey and witness the magic of unlocking angles!

Unlocking the Secrets of Trigonometry: A Step-by-Step Guide to Finding Angles

In the vast tapestry of mathematics, trigonometry stands as a bridge between geometry and calculus. It provides a powerful toolset for understanding the relationships between sides and angles in triangles, empowering us to navigate the world around us.

Understanding Elevation and Depression Angles

Imagine a towering skyscraper, its summit reaching towards the heavens. To determine its height, we can use an angle of elevation, measuring the angle between the horizontal and the line of sight to the top of the building. Similarly, when observing a submarine beneath the ocean’s surface, we employ an angle of depression to calculate its depth. Trigonometry allows us to find these angles with precision.

Exploring the Wonders of Sine, Cosine, and Tangent

Trigonometry revolves around three fundamental trigonometric ratios: sine, cosine, and tangent. These ratios relate the sides of a right triangle to its angles. By understanding how these ratios work, we can unlock the secrets of finding angles.

Unveiling the Step-by-Step Process

Calculating angles using trigonometry is a methodical process that follows these key steps:

1. Identify the Relevant Ratio: Determine which trigonometric ratio (sine, cosine, or tangent) is relevant to the given information.
2. Substitute Known Values: Plug the known side lengths or angles into the chosen trigonometric ratio.
3. Solve for the Unknown: Use algebraic techniques to isolate the unknown angle, calculating its value.

For instance, to find the angle of elevation to the top of a 100-foot-tall building from a distance of 50 feet away, we would use the tangent ratio: tan(θ) = opposite/adjacent = 100’/50′ = 2. Using a calculator, we find that θ = 63.43 degrees.

By mastering these steps, we gain the ability to accurately determine angles in a wide range of real-world scenarios, from construction and surveying to astronomy and navigation.

Unlocking the Secrets of Angles: A Journey Through Trigonometry

Imagine yourself standing at the base of a colossal mountain, gazing upwards in awe. How do you determine its height without scaling its sheer face? Enter the realm of trigonometry, where angles hold the key to unlocking such secrets.

Understanding Elevation and Depression

When you look up at the mountain, you’re measuring an angle of elevation. Similarly, when you look down at a valley, you’re measuring an angle of depression. Understanding these angles is crucial for determining height, distance, and more.

Exploring Sine, Cosine, and Tangent

Meet the trio of trigonometric ratios: sine, cosine, and tangent. These ratios, represented by sin, cos, and tan, are defined by the sides of a right triangle. They connect angles to the lengths of the triangle’s sides.

Special Right Triangles: Your Trigonometry Toolkit

Navigating trigonometry becomes effortless with special right triangles, such as the 30-60-90 and 45-45-90 triangles. These triangles have predetermined trigonometric ratios, making it a breeze to find angles and side lengths.

Unraveling Angles with Trigonometry

Now that you have the tools, let’s unravel angles step-by-step. Identify the relevant trigonometric ratio based on the given information. For instance, if you know the height and distance from the mountain’s base, use the tangent ratio to find the angle of elevation.

Example:

Suppose the mountain’s height is 2000 feet and you’re 1000 feet from its base. Using the tangent ratio:

tan(angle of elevation) = opposite / adjacent
tan(angle of elevation) = 2000 feet / 1000 feet
angle of elevation = arctan(2) ≈ 63.43 degrees

With this angle, you’ve unlocked the mountain’s height without a single climb. Trigonometry empowers you to explore the world’s angles and uncover its hidden dimensions. Embrace this journey, and let the angles guide your understanding of the world around you.