Understanding Triangle Vertices: Types, Labeling, And Significance

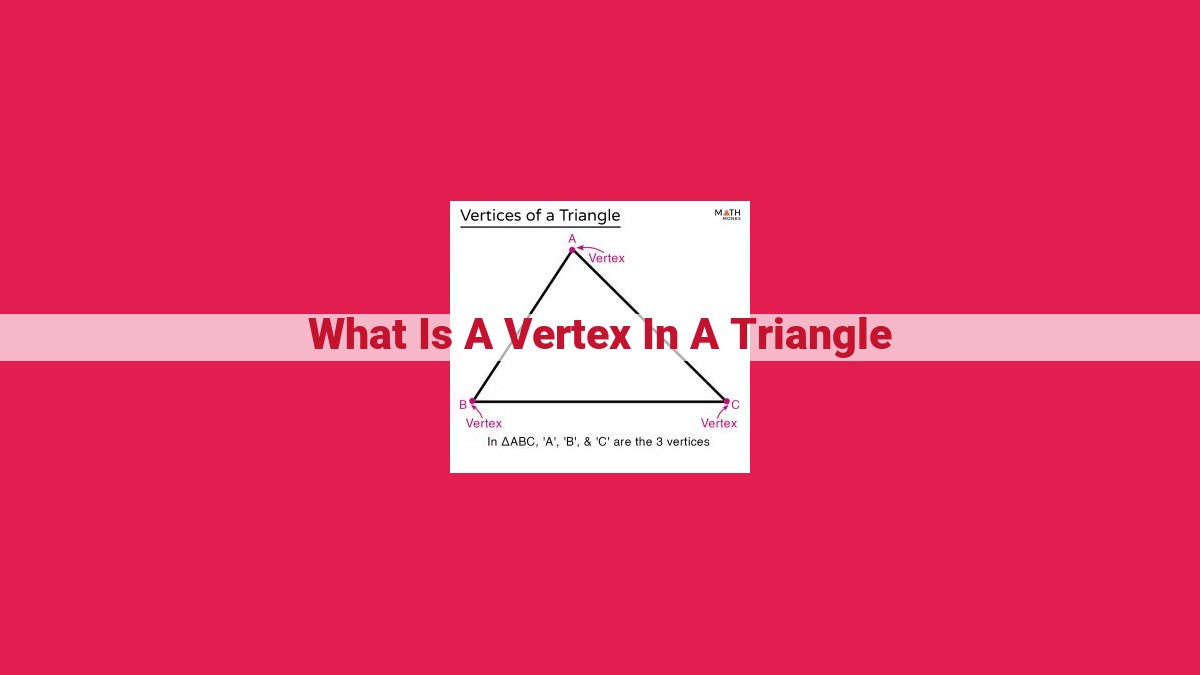
A vertex in a triangle is the point where two sides of the triangle intersect. It is the junction of three line segments and forms an angular point. There are three vertices in a triangle, and they are typically labeled A, B, and C. The vertex at the highest point of the triangle is called the apex. Vertices play a crucial role in defining the shape, size, and angles of a triangle.

Unveiling the Essence of a Vertex: The Cornerstone of a Triangle

In the realm of geometry, triangles reign supreme as the foundation for more complex shapes. At the heart of every triangle lies a crucial element—the vertex. A vertex is the point where two or more sides of a triangle intersect, serving as a fundamental building block that defines the shape’s structure and properties.

The Junction of Lines

Imagine a triangle as a canvas upon which three line segments intersect. At each intersection, a vertex emerges as the point of convergence. These vertices are not mere adornments but essential components that determine the shape and relationships within the triangle.

The Angular Point

As two sides intersect to form a vertex, they create an angle. The vertex acts as the angular point, marking the measure of the angle between the two sides. This angularity is crucial in determining the overall shape and properties of the triangle, such as its classification as acute, right, or obtuse.

The Apex: A Pinnacle of Elevation

In certain triangles, one vertex may stand out as the apex. This is the vertex located at the highest point of the triangle, towering over its counterparts. The apex plays a pivotal role in determining the triangle’s orientation and is often used as a reference point for measurements and calculations.

Additional Subtopics:

• Types of Vertices: Vertices can be classified further based on their position and relationships within the triangle, such as interior, exterior, and concave vertices.
• Vertex Coordinates: Vertices can be represented using coordinates in a two-dimensional plane, providing precise location information within the triangle’s geometry.
• Role in Triangulation: Vertices are fundamental in the process of triangulation, a technique used for determining distances and angles in surveying and navigation.

The Essence of a Vertex: Where Triangle Sides Intersect

In the realm of geometry, a vertex holds a pivotal role as the point where two sides of a triangle meet. Imagine a triangle as a celestial tapestry woven with three distinct threads. At the point where any two of these threads cross, a vertex is born.

Think of the vertex as a celestial weaver, meticulously guiding the threads together to form the intricate angles that define a triangle. It is the point where the boundaries of two sides converge, creating the foundation for the triangle’s shape and structure.

A vertex is not merely a point of intersection but a crucial element in understanding triangle geometry. It serves as the cornerstone upon which angles, side lengths, and area calculations rest, making it a vital concept in the world of mathematics.

Point Where Three Line Segments Meet: Understanding the Vertex of a Triangle

In the realm of geometry, the vertex holds a pivotal role in the formation and properties of triangles. Imagine a triangle as a three-sided figure, each side represented by a line segment. The vertex is the crucial point where these line segments converge, forming the corners of the triangle.

Just as three roads intersect at a junction, the vertex marks the intersection point of two sides of a triangle. These line segments extend from the vertex, creating the characteristic triangular shape. The vertex acts as the meeting ground where the sides unite to form a cohesive whole.

Visualize the vertex as the center of a web, with the line segments radiating outwards like spokes. It is the nucleus that holds the triangle together, providing structural integrity and defining its overall shape and size. Without the vertex, the triangle would simply be three disconnected line segments, lacking the essential connection that defines its geometric form.

Angular Point

• Discuss the concept of a vertex as an angular point, where two sides intersect to form an angle.

Angular Points: The Intersections Where Triangles Take Shape

As we delve deeper into the fascinating world of triangles, we encounter the concept of vertices, those crucial points where two sides intersect to form angles. These angular points serve as the cornerstone of any triangle, shaping its size, shape, and properties.

Imagine a triangle as a canvas upon which three line segments, its sides, meet. At the points where these sides converge, vertices emerge. Each vertex is the result of the intersection of two line segments, creating an angular point.

Vertex and Angle Formation

The intersection of two sides in a triangle forms a vertex. Think of it as a meeting place where two walls join to create a corner. The angle created by these intersecting sides is measured in degrees, and the vertex is the point where the angle’s bisector intersects the triangle’s interior.

In a triangle, there are always three vertices, each corresponding to the meeting point of two sides and forming two angles. The angles at each vertex together sum up to 180 degrees, fulfilling the “angle sum property” of triangles.

The Significance of Angular Points

Vertices play a vital role in determining a triangle’s properties. For instance, the vertex with the smallest angle corresponds to the shortest side in the triangle. Similarly, the vertex with the largest angle corresponds to the longest side.

Furthermore, the angles at a vertex determine the triangle’s overall shape. If all three angles are less than 90 degrees, the triangle is acute. If one angle is exactly 90 degrees, the triangle is right-angled. And if one angle is greater than 90 degrees, the triangle is obtuse.

The Apex: A Special Vertex

In a right-angled triangle, there’s a special vertex known as the apex. It’s the vertex located at the highest point of the triangle, where the two perpendicular sides meet. The apex essentially divides the triangle into two smaller right triangles, each of which has its own properties.

Vertices are the angular points where triangles take shape. They form angles, determine side lengths, and influence the triangle’s overall properties. Understanding vertices is essential for comprehending the fundamental principles of geometry and the fascinating world of triangles.

Delving into the World of Vertices: A Guide to Triangle Fundamentals

In the realm of geometry, understanding vertices is crucial for comprehending the intricacies of triangles. These pivotal points, where sides converge to form angles, play a vital role in defining the shape and properties of this versatile polygon.

Unveiling the Essence of a Vertex

A vertex, often referred to as a corner point, is the juncture where two or more sides of a triangle intersect. It serves as a meeting ground for the line segments that constitute the triangle, giving it its distinctive shape.

The Junction of Sides, the Genesis of a Vertex

When two sides of a triangle meet at a common point, they form a vertex. This intersection creates an angular point, where the sides diverge to create an interior angle. The vertex, therefore, acts as the origin of the angle formed by the two sides.

Three Lines, One Vertex: A Point of Convergence

A vertex can also be described as the point where three line segments, the sides of the triangle, converge. It is this confluence of lines that gives rise to the vertex and establishes the triangle’s overall shape.

Angular Points: Vertices As Angle Generators

Vertices are pivotal in defining the angles of a triangle. The two sides meeting at a vertex form an angle, which is measured in degrees. The sum of the angles in any triangle is always 180 degrees, highlighting the interdependence between vertices and angles.

The Apex: The Triangle’s Peak

In certain triangles, one vertex is located at the highest point, forming the apex. This vertex, often denoted as the peak, is a crucial reference point for measuring the altitude of the triangle, the perpendicular distance from the base to the vertex.