Unveiling The Secrets Of Triangle Calculations: A Comprehensive Guide To Solving Triangle Problems

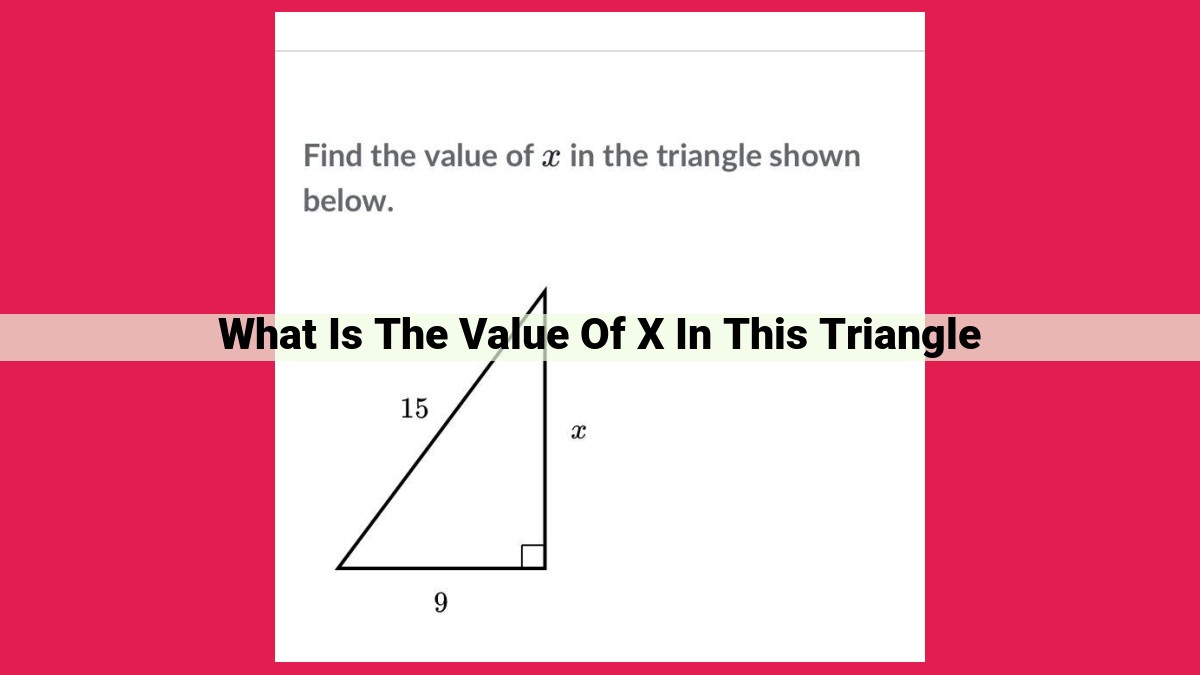
To find the value of x in a triangle, leverage the concepts of similarity, proportions, the Pythagorean theorem, and trigonometry. Similar triangles share congruent angles and proportional side lengths. Using cross-multiplication, we can solve proportions to find unknown side lengths. The Pythagorean theorem helps us determine unknown sides in right triangles. Trigonometry employs sine, cosine, and tangent ratios to calculate unknown sides and angles. By combining these concepts, we can effectively solve triangle problems, unlocking the power of geometric relationships and trigonometric identities.

Finding the Elusive X: Unraveling the Secrets of Triangle Geometry

In the enigmatic world of geometry, triangles hold a special place, often posing intriguing puzzles that require a deft combination of concepts. One such challenge is determining the elusive value of x, a variable that can make or break your solution.

To approach this geometric conundrum with confidence, we must delve into the essential concepts that will serve as our tools:

• Similarity: Triangles that share the same shape but differ in size can reveal valuable insights through their geometric similarities.

• Proportions: Ratios and cross-multiplication become our allies in establishing the hidden relationships between triangle sides.

• Pythagorean Theorem: This cornerstone of geometry holds the key to unlocking side lengths in right triangles.

• Trigonometry: The angles themselves become a source of information through trigonometric ratios, allowing us to bridge the gap between angles and sides.

Together, these concepts form a powerful arsenal that will guide us through the labyrinth of triangle geometry. With patience and a keen eye, we will conquer the enigma of x and emerge victorious in our geometric quest.

Similar Triangles: The Cornerstone of Triangle Problem Solving

In the realm of geometry, triangles often pose intriguing challenges, particularly when it comes to determining the elusive value of x. Embark on a captivating journey as we explore similar triangles, the cornerstone of unlocking the secrets of these enigmatic shapes.

Similar triangles, like kindred spirits, share an enchanting bond of geometric similarity. Congruent angles grace their celestial forms, ensuring perfect alignment in their ethereal dance. Moreover, a mysterious force known as the scale factor unites them, preserving the ratios of their corresponding sides. It’s as if an invisible celestial architect has crafted these triangles in harmonious proportions, a testament to the beauty of mathematical symmetry.

Delving deeper into the world of similar triangles, we uncover a treasure trove of properties that empower us to conquer triangle conundrums. Their congruent angles grant us the ability to establish proportions, which are like magical equations that interweave the corresponding sides of similar triangles. By employing the power of cross-multiplication, we can shatter the shackles of unknown side lengths, liberating them from their mathematical captivity.

The journey to mastery begins with a profound understanding of these fundamental concepts, for they provide the bedrock upon which all triangle problem solving endeavors rest. So, intrepid explorers, embrace the enchanting world of similar triangles, and let their extraordinary powers guide you towards mathematical enlightenment.

Triangle Proportions: The Key to Unlocking Unknown Lengths

In the captivating world of triangles, where angles dance and sides whisper secrets, proportions emerge as the magical wands that reveal their hidden dimensions. Like a compass guiding a ship through a labyrinthine sea, proportions provide us with the tools to navigate the intricacies of triangle geometry.

Proportions: A Balancing Act

Imagine a delicate scale, with one side carrying x units and the other carrying y units. When these values are in perfect balance, we have a proportion. In mathematical terms, this means x/y = a/b, where a and b are constants.

Cross-multiplication: The Key to Unlocking Secrets

Just as a key unlocks a door, cross-multiplication unlocks the secrets hidden within proportions. By multiplying the numerator of the first fraction by the denominator of the second, and vice versa, we can unveil the hidden value of the unknown variable.

For instance, if we have the proportion x/3 = 4/12, cross-multiplication reveals that x = (4 x 3)/12 = 12/12 = 1. Eureka! We have found the value of x.

Proportions in Triangle Geometry: A Symphony of Sides

Proportions play a pivotal role in understanding the relationships between the sides of triangles. Let’s explore a scenario where a triangle has side lengths of x, y, and z.

If the triangle is similar to another triangle with side lengths of a, b, and c, then the following proportions hold true:

• x/a = y/b = z/c

These proportions indicate that the ratios between corresponding sides are proportional. This powerful insight allows us to deduce unknown side lengths by simply solving the proportions.

Example: Unraveling the Mystery

Consider a triangle with side lengths x, 2x, and 3x. If this triangle is similar to another triangle with side lengths of 5, 10, and 15, we can use proportions to find the values of x:

• x/5 = 2x/10 = 3x/15
• Simplifying, we get: x/5 = 1/5
• Multiplying both sides by 5, we finally discover that x = 5.

Proportions are the unsung heroes of triangle geometry, offering a key to unlock the mysteries of length and ratio. By understanding and utilizing proportions, we can unravel the secrets of triangles, conquer any geometry challenge, and leave the unknown behind. Remember, proportions are the wand that transforms triangle geometry from a complex puzzle to a captivating adventure.

The Pythagorean Theorem: Unlocking the Secrets of Right Triangles

Have you ever wondered how to find the missing side of a triangle when you know the lengths of the other two sides? The answer lies in the time-tested Pythagorean theorem, a mathematical tool that has puzzled and fascinated generations of students.

The Mystery of the Right Triangle

Triangles are fascinating shapes with unique properties. Among them is the right triangle, a specific type of triangle with one angle measuring 90 degrees. This special angle sets the stage for the Pythagorean theorem.

Enter Pythagoras

In the ancient world, the Greek mathematician Pythagoras stumbled upon a groundbreaking discovery: the relationship between the lengths of the sides of a right triangle. His theorem, simply put, states that:

The square of the length of the hypotenuse (the longest side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

Represented mathematically as a² + b² = c², where ‘a’ and ‘b’ are the lengths of the legs of the triangle (the sides adjacent to the right angle) and ‘c’ is the length of the hypotenuse.

Using the Theorem

To harness the power of the Pythagorean theorem, follow these steps:

1. Identify the hypotenuse: Determine which side is the longest and forms the opposite side of the right angle.
2. Square the lengths: Calculate the squares of the lengths of the other two sides.
3. Add the squares: Sum up the results obtained in step 2.
4. Take the square root: The result of this operation yields the length of the hypotenuse.

Examples of Pythagorean Perfection

Let’s illuminate the theorem with an example. Suppose you have a right triangle with legs of length 3 and 4 units. To find the length of the hypotenuse:

• Square the leg lengths: 3² = 9 and 4² = 16
• Add the squares: 9 + 16 = 25
• Take the square root: √25 = 5

Therefore, the length of the hypotenuse is 5 units.

The Power of the Theorem

The Pythagorean theorem is an indispensable tool in geometry, architecture, and engineering. It allows us to:

• Determine unknown side lengths of right triangles
• Calculate distances and heights where direct measurements are impossible
• Design structures with precise angles and proportions

Embrace the Pythagorean Legacy

The Pythagorean theorem is more than just a formula. It’s a gateway to unlocking the secrets of triangles and a testament to the enduring power of mathematical principles. By understanding and applying this theorem, you’ll gain a deeper appreciation for the complexities of geometry and the elegance of mathematical relationships.

Trigonometry: The Key to Unlocking Triangle Mysteries

Trigonometry, the branch of mathematics dealing with the relationships between the sides and angles of triangles, plays a pivotal role in determining the value of x in a triangle. By understanding the basics of trigonometry, you can wield a powerful tool to conquer even the most puzzling triangle problems.

Trigonometric Ratios: The Essence of Trigonometry

Trigonometry revolves around the concept of trigonometric ratios: sine, cosine, and tangent. These ratios relate the lengths of the sides of a right triangle to the measures of its angles.

• Sine (sin) is the ratio of the length of the opposite side (the side opposite the angle in question) to the length of the hypotenuse (the longest side of a right triangle).
• Cosine (cos) is the ratio of the length of the adjacent side (the side adjacent to the angle in question) to the length of the hypotenuse.
• Tangent (tan) is the ratio of the length of the opposite side to the length of the adjacent side.

Unveiling the Power of Trigonometric Ratios

These trigonometric ratios serve as a gateway to unlocking triangle secrets. By using the appropriate ratio, you can determine unknown side lengths or angles when you know certain other measures.

For instance, if you know the length of the opposite side and the measure of the angle opposite it, you can use the sine ratio to find the length of the hypotenuse. Similarly, if you know the length of the adjacent side and the measure of the angle adjacent to it, you can use the cosine ratio to find the length of the hypotenuse.

Examples of Trigonometric Triumphs

Let’s consider a few examples to illustrate the power of trigonometry:

• Determining the height of a building: If you know the distance from the base of the building to a point on level ground and the angle between the horizontal and a line of sight to the top of the building, you can use the tangent ratio to calculate the height of the building.
• Navigating a triangle maze: If you know the angles and length of one side of a triangle, you can use trigonometric ratios to determine the lengths of the other two sides and the measures of the other angles, allowing you to navigate the triangle maze with precision.

Trigonometry, with its arsenal of trigonometric ratios, empowers you to solve triangle problems with remarkable accuracy. By grasping these fundamental concepts and applying them with finesse, you can unlock the secrets of triangles and conquer any geometric challenge that comes your way. Embrace the power of trigonometry and become a master of triangle mysteries!