Unveiling The Secrets Of Triangle Angles: Sum, Range, And Triangle Formation
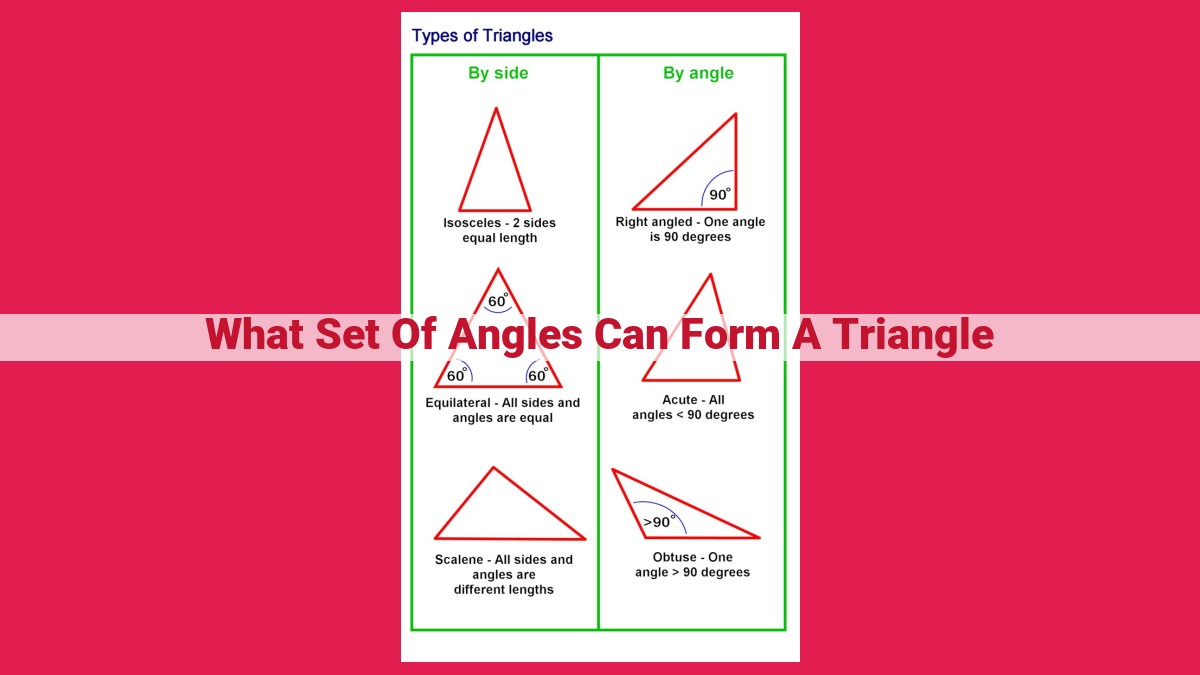
A triangle’s interior angles must follow specific rules to form a valid triangle. The sum of the three angles must be exactly 180 degrees, known as the Angle Sum Property. Additionally, each angle must be less than 180 degrees and greater than zero, as dictated by the Triangle Inequality Theorem. By satisfying these conditions, a set of angles can determine the formation of a triangle, allowing for a deeper understanding of these geometric shapes.
- Definition of a triangle
- Relationship between sides and angles
The world of shapes is vast and intriguing, and among them, triangles hold a special place in the realm of geometry. These three-sided wonders are the foundation of countless structures and objects in our surroundings, from towering skyscrapers to the humble pyramids. Understanding triangles is not just essential for students of mathematics but also for anyone curious about the intricate world of shapes.
Definition of a Triangle
A triangle is a polygon with three sides and three angles. It is the simplest and most basic polygon, yet it possesses remarkable properties. The three sides are typically denoted as a, b, and c, while the angles are represented by A, B, and C. Angles are formed where two sides meet, and sides are the lines that connect the vertices of a triangle.
Relationship Between Sides and Angles
The relationship between the sides and angles of a triangle is a fascinating aspect of their geometry. One key observation is that the sum of the interior angles of a triangle is always 180 degrees. This angle sum property is a fundamental concept that governs the formation of triangles.
Another intriguing relationship is the triangle inequality theorem, which states that the sum of any two sides of a triangle must be greater than the third side. This theorem ensures that a triangle can be successfully formed with the given lengths of its sides.
Understanding the Sum of Interior Angles in Triangles
In the realm of geometry, where shapes dance harmoniously, understanding the intricate details of triangles unlocks a wealth of knowledge. Among the fundamental concepts that define these geometric gems is the sum of their interior angles.
The interior of a triangle is the region bounded by its sides. Intriguingly, the sum of the interior angles of any triangle, no matter its size or shape, always equals 180 degrees. This fascinating property serves as a cornerstone for unraveling the mysteries that shroud triangles.
To grasp this concept, imagine yourself as an intrepid explorer navigating through a triangle’s interior. As you venture along each side, carefully measuring the angles formed at the vertices where they meet, you’ll discover a remarkable pattern. The sum of these interior angles always remains constant – a steadfast 180 degrees.
This phenomenon has its roots in a fundamental theorem known as the triangle sum theorem, which proclaims that the sum of the interior angles of a triangle is always 180 degrees. This theorem provides a powerful tool for solving countless problems involving triangles.
Moreover, the sum of interior angles is inextricably linked to other mathematical concepts, such as parallel lines and supplementary angles. Understanding the relationship between these concepts is paramount for unlocking the full potential of triangle geometry. By delving into the intricacies of angle sums, you’ll not only unravel the secrets of triangles but also gain a deeper appreciation for the harmonious interplay of geometry.
Unraveling the Angle Sum Property of Triangles
In the realm of geometry, triangles captivate our curiosity as some of the most fundamental yet intriguing shapes. They form the building blocks of countless structures, from towering skyscrapers to delicate origami creations. At the heart of understanding triangles lies a remarkable concept known as the Angle Sum Property.
The Definition and Significance of the Angle Sum Property
The Angle Sum Property dictates that the sum of the interior angles of any triangle is always 180 degrees. This holds true for all triangles, regardless of their size, shape, or orientation. It’s a fundamental principle that serves as a cornerstone for many other geometric theorems and concepts.
Implications for Triangle Formation
The Angle Sum Property has profound implications for the formation and validity of triangles. It establishes crucial conditions that govern the possible combinations of angles within a triangle:
- Angle Sum Restriction: The sum of the angles in a triangle cannot exceed 180 degrees. This means that if two angles add up to more than 180 degrees, they cannot form a valid triangle.
- Minimum Angle Condition: The smallest angle in a triangle must be greater than 0 degrees. This ensures that the remaining two angles can sum up to less than 180 degrees, satisfying the Angle Sum Property.
- Maximum Angle Condition: The largest angle in a triangle cannot be greater than 180 degrees. Otherwise, it would dominate the triangle’s interior, leaving no room for the other two angles to meet the Angle Sum Property.
Determining Valid Sets of Angles
Using these conditions, we can determine whether a given set of angles can form a valid triangle:
- Check the Angle Sum Restriction: Add the three angles together. If the sum is greater than 180 degrees, the angles cannot form a triangle.
- Verify the Minimum Angle Condition: Ensure that the smallest angle is greater than 0 degrees.
- Satisfy the Maximum Angle Condition: Confirm that the largest angle is less than 180 degrees.
By adhering to these guidelines, we can accurately assess the validity of any set of angles for triangle formation.
The Angle Sum Property for Triangles is an essential concept that unlocks a deeper understanding of these fascinating shapes. It governs the possible combinations of angles within a triangle, enabling us to determine their validity and explore the intricate relationships between their sides and angles. As we delve further into the world of geometry, this property will continue to guide our investigations and reveal the hidden symmetries and patterns that shape our surroundings.
The Triangle Inequality Theorem: Ensuring Triangle Validity
In the realm of triangles, a fundamental question arises: can any three arbitrary segments form a valid triangle? The answer lies in the Triangle Inequality Theorem, a cornerstone of triangle geometry.
Understanding the Theorem
The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. In other words, for a triangle to be valid, its sides must satisfy the following inequality:
AB + BC > AC
where AB, BC, and AC represent the lengths of the sides.
Applying the Theorem to Verify Validity
The Triangle Inequality Theorem is essential for verifying the validity of triangles. By applying this rule, we can quickly determine whether a given set of side lengths can form a triangle.
For example, let’s consider the following side lengths:
- AB = 5 cm
- BC = 7 cm
- AC = 9 cm
Using the Triangle Inequality Theorem, we have:
AB + BC > AC
5 cm + 7 cm > 9 cm
12 cm > 9 cm
Since the sum of AB and BC is greater than AC, we can conclude that these side lengths satisfy the Triangle Inequality Theorem. Therefore, the given side lengths form a valid triangle.
Implications for Triangle Formation
The Triangle Inequality Theorem has profound implications for understanding triangle formation. It establishes that the sides of a triangle are not independent. There are limitations on the possible combinations of side lengths that can form a triangle.
Specifically, the theorem implies that the greatest side of a triangle must be shorter than the sum of the other two sides. This constraint ensures that triangles can be formed with a wide range of side lengths but not with arbitrary ones.
By understanding and applying the Triangle Inequality Theorem, we gain a deeper appreciation for the geometry of triangles and the intricate relationships between their sides.
Determining Valid Sets of Angles for Triangles
In the world of geometry, triangles reign supreme as one of the most fundamental shapes. Understanding the intricacies of triangles is crucial, and one key aspect is determining whether a set of angles can form a valid triangle. Let’s embark on a storytelling journey to unravel the secrets behind this intriguing concept.
The Angle Sum Property: A Guiding Light
Imagine a triangle as a harmonious trio of angles. The Angle Sum Property whispers a profound truth: “The sum of the interior angles of a triangle is always 180 degrees.” This property serves as a beacon, guiding us towards understanding the possibilities and limitations of triangle formation.
Steps to Assess Angle Validity
Now, let’s don our detective hats and embark on a step-by-step investigation to determine the validity of angle sets:
- Sum the Angles: Add up the three angles. If the result is exactly 180 degrees, you have a valid set.
- Check Triangle Inequality: Recall the Triangle Inequality Theorem. It states that the sum of any two sides of a triangle must be greater than the length of the third side. This principle also applies to angles: the sum of any two angles must be less than 180 degrees.
- Examine Individual Angles: Each angle should be greater than 0 degrees and less than 180 degrees. An angle of 0 degrees or 180 degrees would result in a degenerate triangle, not a true triangle.
Considerations for Triangle Validity
As we delve deeper, we encounter a few additional considerations:
- Positive Angles Only: Angles must be positive values. Negative angles have no place in the realm of triangles.
- No Redundant Angles: Each angle should be unique. Triangles cannot have two or more identical angles (except for equilateral triangles, but that’s a story for another day).
Putting It All Together
Determining valid angle sets for triangles is like solving a puzzle. By following these steps and considering the key concepts discussed, you can become a master triangle detective. Remember, the Angle Sum Property is your unwavering companion, and the Triangle Inequality Theorem ensures that your triangles have integrity.
Mastering these concepts will empower you to navigate the world of triangles with confidence, unlocking a treasure trove of geometrical knowledge.