Triangle Angle Theorems: Understanding Angle Relationships For Shape Properties

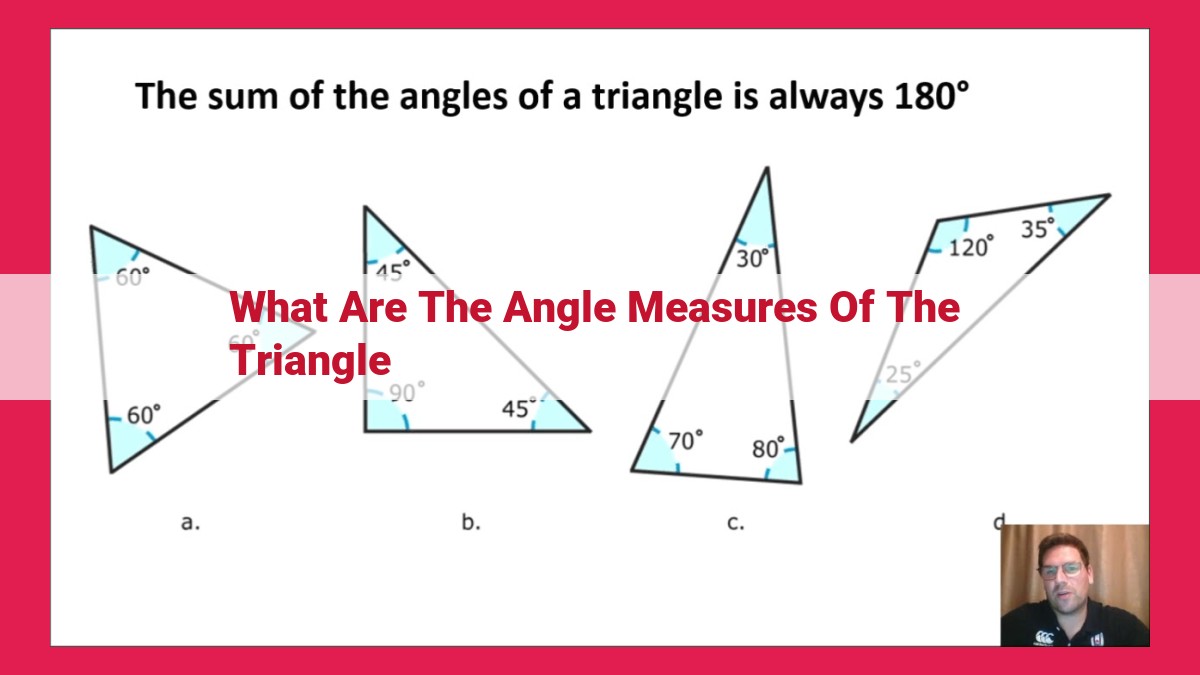
The angle measures in a triangle are crucial for understanding its shape and properties. The sum of the interior angles of a triangle is always 180 degrees, regardless of its size or shape. This is known as the triangle angle sum theorem. Exterior angles are formed when one side of a triangle is extended. An exterior angle is equal to the sum of the two non-adjacent interior angles. Special cases of triangles have specific angle measures, such as equilateral triangles with all angles equal to 60 degrees, 30-60-90 triangles with one angle measuring 90 degrees, and 45-45-90 triangles with two angles measuring 45 degrees. These angle measures can be applied to calculate the area, perimeter, and other properties of triangles.

Understanding the Essence of Triangles: The Foundation of Geometry

Embark on a Geometrical Adventure

In the realm of geometry, triangles reign supreme as one of the most fundamental shapes. These three-sided figures have captivated mathematicians for centuries, forming the bedrock of countless theorems and applications. Join us on an exploration to unravel the mysteries of triangles, beginning with their very definition.

Defining Triangles: The Building Blocks of Geometry

A triangle is a polygon characterized by three straight sides that meet at three distinct points, known as vertices. Each side of a triangle is a line segment that connects two vertices, while the intersection of two sides forms an angle. These angles play a crucial role in classifying triangles and determining their unique properties.

Essential Elements: Sides and Angles

The sides of a triangle are often labeled with lowercase letters (a, b, c), while the angles opposite these sides are denoted by uppercase letters (A, B, C). The sum of the interior angles of any triangle is always 180 degrees. This fundamental theorem provides a cornerstone for understanding and manipulating triangles in various geometrical applications.

Types of Triangles by Side Lengths

• Explain how triangles are classified as equilateral, isosceles, or scalene.

Types of Triangles by Side Lengths

When it comes to triangles, the lengths of their sides play a crucial role in classifying them into different types. Let’s dive into this intriguing world of triangles, exploring the characteristics and names associated with each type.

Equilateral Triangles: The Realm of Perfect Balance

In the realm of triangles, equilateral triangles stand out with their exceptional symmetry. All three sides of an equilateral triangle are equal in length, making them the epitome of balance and harmonious proportions. This remarkable equality extends to their angles, which are all 60 degrees.

Isosceles Triangles: Twins with a Twist

Isosceles triangles, while sharing the characteristic of equal sides, differ from equilateral triangles in a subtle yet significant way. Two sides of an isosceles triangle are equal in length, forming a congruent pair. The remaining side, the base, distinguishes it from its identical siblings. The angles opposite the equal sides are also equal, maintaining a sense of symmetry.

Scalene Triangles: Embracing Diversity

In the vibrant world of triangles, scalene triangles embrace individuality. All three sides of a scalene triangle have different lengths, making it the most diverse type. Each angle is also distinct, giving scalene triangles an asymmetrical charm.

So, there you have it – the captivating world of triangles by side lengths. From the equilateral triangle’s perfect symmetry to the distinctive asymmetry of the scalene triangle, each type holds its own unique beauty and significance. Next time you encounter a triangle, take a closer look and see if you can identify its type based on its side lengths.

Types of Triangles by Angle Measures

Discover the Secrets of Triangle Angles:

In the realm of geometry, triangles stand out as enigmatic shapes, their angles holding the key to their identities. Just as humans are classified by their unique traits, triangles are categorized according to the measures of their angles. Let’s embark on a journey to unravel the secrets of acute, right, and obtuse triangles.

Embracing Acute Triangles

Acute triangles embody youth and exuberance, their bright angles dancing within a vibrant range of 0 to 90 degrees. Like cheerful children filled with endless curiosity, acute triangles exude a sense of adventure and exploration.

Standing Tall with Right Triangles

Right triangles, the epitome of stability and purpose, boast a singular angle that boldly claims 90 degrees. This angle, the cornerstone of the triangle, acts as a beacon of order and precision. Right triangles carry themselves with an air of confidence, their angles working in perfect harmony to create a stable foundation.

Encountering Obtuse Triangles

Obtuse triangles, the enigmatic guardians of the triangle realm, possess a single angle that soars beyond 90 degrees. These triangles exude an aura of mystery and intrigue, their angles whispering tales of distant lands. Obtuse triangles challenge our preconceived notions, pushing the boundaries of what we know about triangles.

Unveiling the Significance of Angles:

The angles of a triangle are not mere curiosities; they hold immense power. The sum of the interior angles of any triangle remains constant at 180 degrees, regardless of its size or shape. This holds true whether the triangle is an energetic acute triangle, a composed right triangle, or an enigmatic obtuse triangle.

Additionally, the angles of a triangle offer a glimpse into its other properties. By studying the angles, we can uncover the secrets of the triangle’s perimeter, its area, and even its shape.

Unlocking the Potential of Angle Measures:

The angles of triangles are not just labels; they are tools that empower us to explore the vast world of geometry. From determining the area of a triangle to calculating its perimeter, angle measures provide the key to unlocking the hidden secrets of these captivating shapes.

Angle Measures in a Triangle: Unraveling the Secrets of Triangular Geometry

Embrace the journey as we delve into the captivating world of triangle angle measures. From the fundamental theorem that governs their sum to the intriguing concept of exterior angles, our exploration will paint a vivid picture of these intriguing geometric shapes.

The Sum of Interior Angles: A Guiding Principle

In the realm of triangles, a cornerstone theorem dictates that the sum of the interior angles, those found within the triangle, is a constant value. This pivotal value, 180 degrees, serves as the compass guiding our understanding of these angles. Whether you encounter an equilateral triangle with congruent angles or a scalene triangle with distinct angle measures, this theorem holds true.

Exterior Angles: A Gateway to New Perspectives

Venturing beyond the triangle’s interior, we encounter the concept of exterior angles, formed when one side of a triangle is extended. These angles provide a novel vantage point on the triangle’s geometry. To determine the measure of an exterior angle, simply subtract the measure of its adjacent interior angle from 180 degrees.

By understanding the relationship between interior and exterior angles, we unlock a treasure trove of insights into triangles. These measures empower us to tackle complex problems, such as finding the area of a triangle using the 1/2bh formula or employing trigonometric identities to calculate its perimeter.

Harnessing Angle Measures for Unlocking Triangular Secrets

The interplay of angle measures empowers us to unlock the secrets that triangles hold. Embark on an expedition of discovery, where you’ll navigate the intricacies of equilateral triangles with equal angles, unravel the mysteries of 30-60-90 and 45-45-90 triangles, and harness the power of angle measures to conquer any triangular challenge that comes your way.

Special Cases of Triangle Interior Angles

Triangles hold a fascinating world of geometry, and their interior angles paint a canvas of unique patterns. Among all triangles, equilateral, 30-60-90, and 45-45-90 triangles stand out as special cases, showcasing remarkable relationships between their angles.

Equilateral Triangles: Symmetry in Angles

In the realm of triangles, equilateral triangles reign supreme with three equal sides. This symmetry extends to their angles as well – each interior angle measures a perfect 60 degrees. The sum of these angles, as we know, is a staple of geometry: 180 degrees. Like three harmonious notes in a chord, the 60-degree angles resonate with balance and beauty.

30-60-90 Triangles: Right and Special

30-60-90 triangles, also known as half-equilateral triangles, hold a special place in geometry. Their angles exhibit a captivating pattern: one angle measures 30 degrees, another 60 degrees, and the remaining one is a glorious right angle at 90 degrees. This unique configuration makes them ideal for exploring trigonometric ratios and solving real-world problems.

45-45-90 Triangles: Isosceles and Practical

45-45-90 triangles, also known as isosceles right triangles, possess two angles that measure 45 degrees and one that measures 90 degrees. This symmetry in angles makes them useful in various applications, from construction to navigation. The Pythagorean theorem finds its home in these triangles, providing a path to calculate unknown side lengths.

Applications of Angle Measures

The angle measures in these special cases of triangles extend beyond theoretical knowledge. They find practical applications in diverse fields, such as:

• Area Calculations: The 1/2 * b * h formula, where b is the base and h is the height, relies on angle relationships to determine the area of a triangle.

• Perimeter Estimation: Trigonometric identities leverage angle measures to estimate the perimeter of triangles, especially when not all side lengths are known.

In conclusion, the interior angles of equilateral, 30-60-90, and 45-45-90 triangles are not just mathematical curiosities but keys to unlocking geometric insights and solving practical problems. Their unique patterns and applications make them indispensable tools in the world of geometry.

Applications of Triangle Angle Measures

Understanding triangle angle measures opens up a world of possibilities for solving geometrical problems. By skillfully wielding these measurements, we can unlock the secrets of triangles, including their area and perimeter.

Determining Area with the 1/2bh Formula

Like a master surveyor, the 1/2bh formula empowers us to calculate the area of a triangle with ease. Here, “b” represents the base, the side upon which the triangle rests, and “h” symbolizes the height, the perpendicular distance from the vertex opposite the base to the base itself.

Simply multiply half the base length by the height, and voila! You’ve determined the area of your triangle, the space it encompasses within its three sides. This formula is a fundamental tool in geometry, providing a quick and accurate method for finding the area of any triangle.

Unlocking Perimeter with Trigonometry

Trigonometry, the study of triangles and their angles, offers another avenue for calculating the perimeter of a triangle. By utilizing trigonometric identities, we can relate the side lengths to the angle measures and derive formulas for finding the perimeter.

One such identity, the Law of Cosines, provides a versatile equation that can be applied to any triangle. It expresses the relationship between the lengths of two sides, the angle between them, and the third side. By skillfully wielding this law, we can determine the perimeter of even complex triangles, where not all sides or angles are known.

Unveiling the secrets of triangle angle measures empowers us to solve a myriad of geometrical puzzles. Be it determining the area using the 1/2bh formula or unlocking the perimeter with trigonometry, these techniques provide a powerful toolkit for any aspiring geometer or math enthusiast. So, embrace the angles of triangles, and let them guide you on your journey towards geometrical mastery!