Mastering Total Momentum: A Comprehensive Guide To Conservation, Impulse, And System Dynamics

To find the total momentum of a system, first understand the conservation of momentum principle, which states that the total momentum within a closed system remains constant. Then, calculate the impulse applied to the system, which is the change in momentum. Use Newton’s Second Law to relate force, mass, and acceleration to momentum changes. Mass and velocity play crucial roles in determining the magnitude and direction of momentum. Finally, consider the momentum vector, which includes both magnitude and direction, to represent the object’s momentum and calculate the total momentum by summing the momentum vectors of all objects in the system.

• Define momentum and explain its importance in physics.
• State the key concepts that will be discussed: conservation of momentum, impulse, Newton’s Second Law, mass, velocity, and momentum vector.

Unraveling the Enigma of Total Momentum

Momentum, the elusive yet fundamental concept in physics, holds the key to understanding the intricate dance of moving objects. It encapsulates both the magnitude and direction of an object’s motion, providing a comprehensive measure of its “oomph.”

In this exploration, we’ll delve into the fascinating world of total momentum, unearthing its essential components and the laws that govern its behavior. From the conservation of momentum to Newton’s Second Law, we’ll unravel the tapestry of forces, mass, and velocity that shape the destiny of moving entities.

Along the way, we’ll uncover the secrets of impulse, the force that propels momentum shifts. We’ll investigate the profound influence of mass, the unwavering resistance to acceleration. And we’ll dissect the intricate dance of velocity, its magnitude and direction dictating momentum’s path.

Understanding the Law of Conservation of Momentum

In the world of physics, momentum, the product of mass and velocity, governs the motion of objects. The law of conservation of momentum is a fundamental principle that states that the total momentum of an isolated system remains constant in the absence of external forces.

This law is analogous to a game of pool. When you strike a cue ball into a group of stationary balls, the total momentum of the system remains unchanged, even though the individual balls scatter in different directions. The momentum of the cue ball transfers to the other balls, setting them in motion.

The law of conservation of momentum extends beyond billiard balls. It applies to countless real-world phenomena. Consider a rocketship expelling exhaust gases to propel itself forward. As the gases escape the rocket, they carry momentum away from it, propelling the rocket in the opposite direction. The total momentum of the rocket and expelled gases remains constant.

Another example is a pendulum. As the pendulum swings forward, it gains momentum. At the peak of its swing, its velocity momentarily becomes zero, but its momentum is at its maximum. As the pendulum swings back down, its momentum gradually decreases until it reaches its original position. Again, the total momentum of the system (pendulum and Earth) remains constant.

The law of conservation of momentum is a powerful tool for understanding and predicting the motion of objects in countless situations. It is a testament to the fundamental principle that momentum, like energy, can neither be created nor destroyed, only transformed and transferred.

Impulse: The Catalyst for Momentum Change

In the realm of physics, where motion reigns supreme, understanding momentum is pivotal. And while the conservation of momentum ensures that the total momentum of a system remains constant, it’s the impulse that acts as the key player in changing that momentum.

Impulse, denoted by J, is a physical quantity that measures the change in momentum. It arises from the interaction of a force acting on an object over a specific time interval. Mathematically, it’s defined as the product of force (F) and the time interval (Δt) over which the force is applied:

J = F * Δt

Just as a gentle push can propel a ball into motion, impulse can alter the momentum of any object. Think of a rocket launch, where the massive thrust of the engines exerts a force on the rocket over a prolonged time, generating a colossal impulse that propels the rocket into the boundless expanse.

Force and time serve as complementary factors in determining the magnitude of impulse. A stronger force or a longer time interval can amplify the impulse, leading to a more significant change in momentum. Conversely, a weaker force or a shorter time interval will result in a lesser impulse.

Examples of impulse in action are abundant in our world:

• A baseball bat imparts a powerful impulse to the ball, sending it soaring through the air.
• A soccer player kicks the ball with a swift motion, imparting an impulse that propels it toward the goal.
• A seatbelt in a car exerts an impulse to restrain passengers in the event of a collision, minimizing injuries.

Understanding impulse is essential for comprehending the dynamics of motion. It’s a forceful concept that drives momentum change, making it an indispensable tool in physics and engineering.

Newton’s Second Law: A Keystone to Unlocking Momentum

Momentum, a fundamental concept in physics, measures the motion of an object in relation to its mass and velocity. Understanding the principles behind momentum is crucial for unraveling the dynamics of the universe. Newton’s Second Law serves as a cornerstone in this pursuit, providing a powerful tool to calculate momentum and unravel its mysteries.

Newton’s Second Law proclaims that the force acting on an object is directly proportional to its mass and acceleration. In simpler terms, the greater the mass of an object, the more force is required to accelerate it. Conversely, the greater the acceleration applied to an object, the more force is exerted upon it.

Mass: The Inertia Factor

Mass plays a pivotal role in determining an object’s momentum. It represents the object’s inertia, its resistance to changes in motion. An object with a large mass will possess greater inertia and require more force to alter its motion. Conversely, an object with a smaller mass will have less inertia and be more easily accelerated.

Acceleration: The Catalyst for Momentum Change

Acceleration is the rate at which an object’s velocity changes over time. It acts as the catalyst for altering an object’s momentum. When a force is applied to an object, it causes the object to accelerate, thereby changing its velocity and, consequently, its momentum.

Newton’s Second Law in Action: Unveiling Momentum

Newton’s Second Law provides a mathematical equation that directly links force, mass, and acceleration: F = ma. This equation can be rearranged to solve for momentum, which is the product of mass and velocity: p = mv. By knowing the force applied to an object and its mass, we can calculate its momentum using Newton’s Second Law.

This understanding of momentum serves as a cornerstone for exploring a wide range of physical phenomena, from the motion of celestial bodies to the dynamics of collisions. By harnessing the principles of Newton’s Second Law, scientists and engineers can analyze and predict the behavior of objects in motion, unlocking the secrets of our ever-fascinating universe.

Mass: The Inertia-Bearer in Momentum Calculations

In the realm of physics, mass reigns supreme as the determinant of an object’s inertia, its reluctance to accelerate or change its state of motion. This fundamental property plays a crucial role in the calculation of momentum, a measure of an object’s motion.

Momentum, often symbolized by the letter p, is a vector quantity that incorporates both the mass (m) and velocity (v) of an object. It represents the propensity of an object to keep moving in a specific direction.

The greater the mass, the stronger the inertia, and the more resistant the object is to changes in its motion. Imagine a massive boulder and a small pebble. If you try to push them with the same force, the boulder will barely budge, while the pebble will readily accelerate. This is because the boulder’s greater mass gives it a higher inertia.

Mass also influences an object’s momentum. For objects with the same velocity, the heavier object will have a larger momentum. Think of two cars traveling at the same speed. The heavier car will have more difficulty stopping or changing its direction due to its greater momentum.

In summary, mass is an indispensable factor in calculating the total momentum of an object. Its role in determining inertia and influencing momentum makes it a fundamental concept in understanding the motion of objects.

Velocity: A Key Ingredient in Momentum Calculations

Momentum, a crucial concept in the realm of physics, depends heavily on velocity, the rate at which an object changes its position. Velocity is not merely a measure of how fast an object is moving (speed); it also encompasses the object’s direction of motion.

The Dance of Magnitude and Direction

Momentum is a vector quantity, meaning it has both magnitude and direction. The magnitude of momentum is determined by an object’s mass and its speed, while the direction is governed by the object’s velocity. This means that the velocity of an object not only influences the strength of its momentum but also its orientation.

The Role of Velocity in Momentum

Consider two objects with equal mass. If one object is traveling at a higher velocity than the other, its momentum will be greater. This is because the object’s increased velocity contributes to a higher magnitude of momentum. Additionally, if the object’s velocity is in a different direction, its momentum vector will also be different, indicating a change in the direction of motion.

Real-World Examples

In the world of sports, velocity plays a vital role in determining the momentum of players. A football player running with the ball at a high velocity has greater momentum than a player jogging with the ball at a lower velocity. Likewise, a baseball pitcher who throws the ball at a high velocity imparts more momentum to the ball than a pitcher who throws it at a slower velocity.

Understanding the concept of velocity is essential for accurately calculating the total momentum of a system. By considering both the magnitude and direction of velocity, we can gain a deeper understanding of the forces and interactions that govern the motion of objects.

The Momentum Vector: Unraveling the Direction and Strength of Motion

Momentum, a key concept in physics, captures the essence of an object’s motion, encompassing both its mass and velocity. To delve deeper into this concept, we introduce the momentum vector, a powerful tool that not only quantifies the magnitude of momentum but also reveals its direction.

Imagine a moving object, a ball propelled across a field. Its momentum is a vector quantity, meaning it possesses both magnitude and direction. The magnitude of the momentum vector represents the strength or intensity of the object’s motion, while its direction indicates the path the object is following.

The momentum vector is a crucial element in analyzing object motion. By understanding the vector’s magnitude and direction, scientists and engineers can predict how an object will behave in various scenarios. For instance, in a collision, the momentum vector provides insights into the impact’s force and direction, helping researchers delve into the intricacies of the interaction.

Let’s illustrate the significance of the momentum vector with an example. Consider a car moving east at a velocity of 20 m/s. The momentum vector for this car would have a magnitude of 20 kg m/s (mass of the car multiplied by its velocity) and would point directly east.

By considering the momentum vector, we gain a comprehensive understanding of the car’s motion. We not only know its speed but also its direction, allowing us to make informed predictions about its trajectory. This information is invaluable in fields such as physics, engineering, and robotics, where accurate motion analysis is paramount.

In essence, the momentum vector is an essential tool in the realm of physics. It unveils the complete picture of an object’s motion, providing a deeper understanding of how objects interact with their surroundings and enabling us to harness the power of momentum in countless applications.

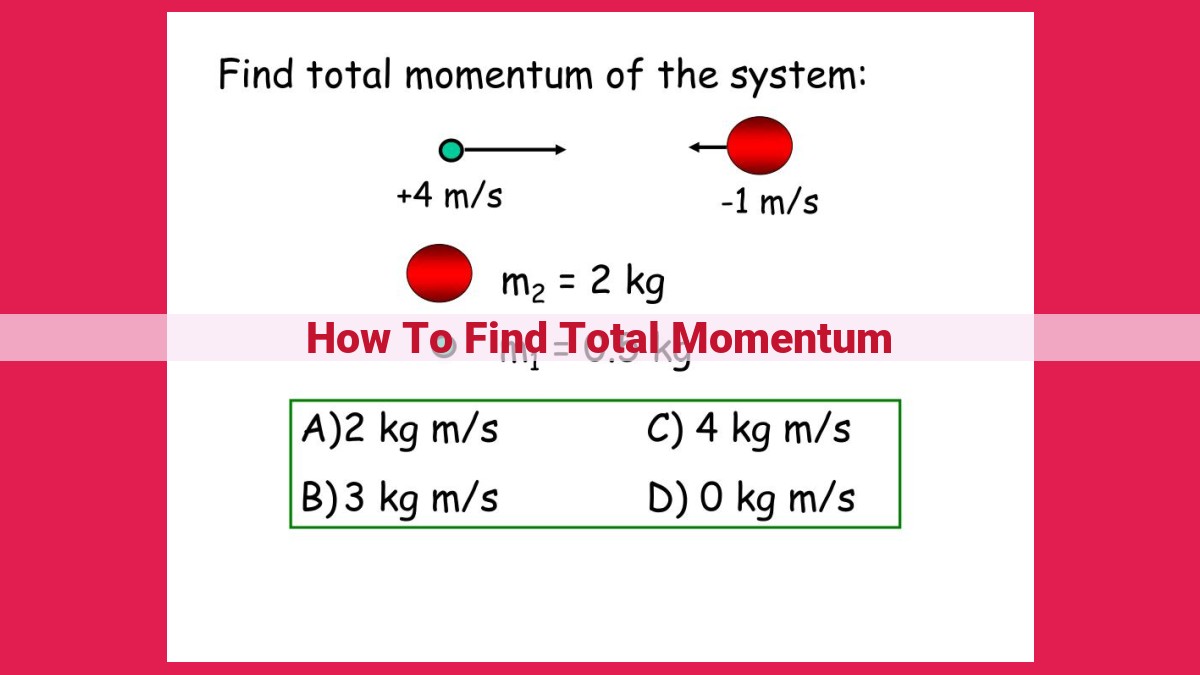
Calculating Total Momentum:

• Explain the steps involved in calculating the total momentum of a system.
• Discuss the factors that need to be considered in the calculation.
• Provide examples of how to calculate total momentum in different scenarios.

Calculating Total Momentum: The Key to Understanding Object Motion

In the realm of physics, momentum is a fundamental concept that describes the motion of objects. It encompasses both the mass and velocity of an object, providing a comprehensive measure of its movement. To delve into this fascinating concept, let’s embark on a journey to understand how to calculate total momentum.

Step 1: Understanding Conservation of Momentum

Momentum is a conserved quantity, meaning that the total momentum of a closed system remains constant, regardless of the interactions within the system. This principle, known as the law of conservation of momentum, forms the basis of our calculations.

Step 2: Momentum as a Vector Quantity

Momentum is a vector quantity, meaning it has both magnitude and direction. The magnitude of momentum is determined by the mass and velocity of the object, while the direction indicates the direction of its motion. This vector nature is crucial for understanding the dynamics of object interactions.

Step 3: Formula for Total Momentum

To calculate the total momentum of a system, we simply add the momentum of each object in the system. The mathematical formula is:

P_total = m₁v₁ + m₂v₂ + ... + mₙvₙ

where:

• P_total is the total momentum of the system
• m₁-mₙ are the masses of each object
• v₁-vₙ are the velocities of each object

Step 4: Considering External Forces

In real-world scenarios, systems are often subject to external forces. These forces can alter the momentum of the system. To account for these forces, we use Newton’s Second Law, which states that:

F = ΔP/Δt

where:

• F is the external force acting on the system
• ΔP is the change in momentum of the system
• Δt is the time interval over which the force acts

Step 5: Examples of Total Momentum Calculations

Let’s consider a few examples to solidify our understanding:

• Example 1: Two cars of masses 1000 kg and 1500 kg are moving in the same direction with velocities of 20 m/s and 30 m/s, respectively. The total momentum of the system is:

P_total = (1000 kg)(20 m/s) + (1500 kg)(30 m/s) = 70,000 kg·m/s

• Example 2: A ball of mass 0.2 kg is thrown vertically upward with a velocity of 10 m/s. At the highest point of its trajectory, its velocity is zero. The change in momentum of the ball is:

ΔP = (0 kg·m/s) - (0.2 kg)(10 m/s) = -2 kg·m/s

Calculating total momentum is a crucial skill in understanding the dynamics of object motion. By considering factors such as mass, velocity, and external forces, we can accurately determine the momentum of a system and predict its behavior. Whether analyzing the interactions of celestial bodies or designing engineering systems, the concept of momentum remains a cornerstone of our understanding of the physical world.