The Circle: An Infinite Canvas Of Symmetry
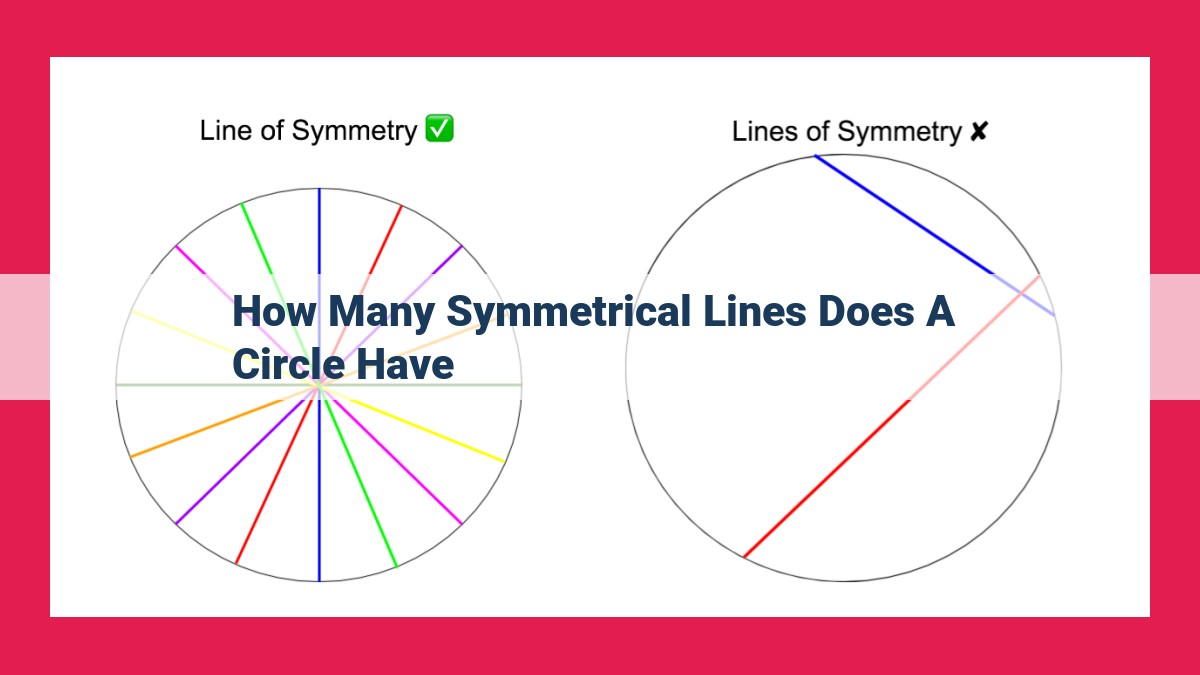
A circle possesses an infinite number of symmetrical lines due to its unique geometric properties. Every diameter drawn through the center of a circle divides the shape into two congruent halves, creating a line of symmetry. Since a circle has an infinite number of possible diameters, it follows that it also has an infinite number of lines of symmetry. This remarkable characteristic stems from the circle’s inherent symmetry and its lack of distinct vertices or edges.
- Hook and thesis statement: Explain the topic and the main point of the blog post.
In the realm of geometry, symmetry reigns supreme as an enchanting concept that shapes our understanding of the world around us. From the delicate petals of a flower to the intricate patterns of a snowflake, symmetry captivates us with its harmonious balance. This blog post will delve into the captivating world of symmetry, revealing its significance in geometry and highlighting its ubiquitous presence in the world we inhabit.
Understanding Symmetry: The Essence of Geometric Harmony
Symmetry, a cornerstone of geometry, refers to the property of a figure that allows it to be divided into two or more identical parts that mirror each other. This division can occur via reflection (flipping) or rotation (turning). Understanding different types of symmetry will pave the way for exploring the fascinating world of geometric shapes.
Line of Symmetry: Splitting Shapes into Symmetrical Halves
A line of symmetry is a line that divides a figure into two congruent parts that are mirror images of each other. Identifying lines of symmetry is crucial for understanding the symmetry of various shapes. From simple triangles to complex polygons, lines of symmetry help us analyze and appreciate the balance and harmony within geometric figures.
Symmetry in a Circle: Embracing Infinite Perfection
A circle stands out as a unique geometric shape that embodies perfect symmetry. Every diameter of a circle creates a line of symmetry, resulting in an infinite number of lines of symmetry. This distinctive feature underscores the circle’s exceptional symmetry and establishes it as a paragon of geometric harmony.
Geometry of a Circle: Unifying Symmetry and Geometric Properties
A circle, defined as a closed plane figure consisting of all points equidistant from a fixed point (the center), possesses unique geometric properties. Its radius (distance from the center to any point on the circle) and diameter (length of a line segment passing through the center and joining two points on the circle) play vital roles in understanding the circle’s symmetry. These properties intertwine to reveal the intricate relationship between symmetry and the geometry of a circle.
Understanding Symmetry in Geometry
Symmetry: A Concept of Harmony
In the world of geometry, symmetry plays a crucial role, adding beauty and order to shapes and figures. Symmetry, in essence, refers to the balanced distribution of elements within a figure, creating a sense of equality and repetition. This concept is not only visually pleasing but also holds mathematical significance, helping us understand the properties and relationships within geometric shapes.
Types of Symmetry: Reflection and Rotation
Symmetry manifests itself in various forms, the two primary types being reflection symmetry and rotational symmetry. Reflection symmetry occurs when a figure can be folded along a line (line of symmetry) to create two congruent mirror images. Imagine a butterfly with its wings spread symmetrically across a central axis.
Rotational symmetry, on the other hand, occurs when a figure can be rotated around a fixed point (center of rotation) without changing its appearance. Consider a circle, which exhibits rotational symmetry around its center regardless of the angle of rotation.
Identifying Lines of Symmetry: A Guide to Dividing Shapes with Precision
In the realm of geometry, symmetry plays a captivating role, creating harmonious patterns and revealing hidden mathematical relationships. Among the various types of symmetry, one that stands out for its elegance and simplicity is line symmetry.
Defining Line of Symmetry: A Guiding Line
In its essence, a line of symmetry bisects a shape into two mirror-image halves. Imagine folding the shape along this line, and you’ll notice that both sides align perfectly. The line of symmetry is the backbone of the shape’s symmetrical structure.
Unveiling Line Symmetry in Various Shapes
Identifying lines of symmetry is a skill that can be honed through observation and practice. Let’s explore different types of symmetrical shapes and unravel the secrets of their lines of symmetry:
- Rectangle: This trusty shape boasts two perpendicular lines of symmetry, reflecting its four congruent sides.
- Square: A square, being a special case of a rectangle, also has two lines of symmetry, intersecting at its center.
- Triangle: Some triangles, known as isosceles triangles, have a single line of symmetry bisecting the base.
- Circle: The circle, a paragon of symmetry, possesses an infinite number of lines of symmetry that pass through its center.
Identifying Lines of Symmetry: A Step-by-Step Guide
- Fold the Shape: Take the shape and fold it in half along a suspected line of symmetry.
- Check for Matching Parts: If the two halves align perfectly, you’ve identified a line of symmetry.
- Repeat the Process: Try folding the shape along different lines to discover other lines of symmetry, if any.
Line symmetry is a fundamental concept in geometry, providing a framework for understanding shape and order. It helps us in:
- Classifying Shapes: Lines of symmetry can be used to classify shapes based on their symmetry properties.
- Solving Geometry Problems: Symmetry can simplify geometric proofs and constructions.
- Creating Balanced Designs: In architecture, art, and design, lines of symmetry contribute to visual harmony and aesthetic appeal.
Symmetry in a Circle
In the realm of geometry, symmetry holds a prominent position, defining the beauty and balance of shapes. Among all shapes, the circle stands out as a perfect example of symmetry.
A circle is a symmetrical shape with respect to any of its diameters. This means that if you were to draw a line through the center of a circle, dividing it into two equal halves, both halves would be mirror images of each other. This is because every diameter of a circle divides it into two congruent halves.
To understand this concept more deeply, let’s take an example. Imagine a circle with a diameter drawn through its center. Now, let’s fold the circle along this diameter. The two halves of the circle will perfectly match, indicating the presence of symmetry.
The reason for this symmetry lies in the very nature of a circle. A circle is defined as the set of all points that are equidistant from a fixed point (the center). This definition implies that for any point on a circle, there is a corresponding point on the opposite side of the circle that is the same distance from the center. This property ensures that any diameter divides the circle into two congruent halves.
Therefore, a circle can be considered a perfectly symmetrical shape, where every diameter creates a line of symmetry, resulting in an infinite number of lines of symmetry. This symmetry makes the circle a fascinating subject of study in geometry, showcasing the beauty and elegance of mathematical concepts.
Infinite Lines of Symmetry in a Circle
- Infinite diameters: Explain that a circle has an infinite number of diameters.
- Infinite lines of symmetry: Explain how each diameter creates a line of symmetry, resulting in an infinite number of lines of symmetry.
Infinite Lines of Symmetry in a Circle: A Geometric Wonder
Picture a perfect circle, its smooth edges and graceful curves captivating your gaze. What you may not realize is that this seemingly simple shape holds a hidden geometric treasure: an infinite number of lines of symmetry.
Let’s explore the secret behind this fascinating property. A diameter is a straight line that passes through the center of a circle and connects two points on its circumference. Now, imagine rotating this diameter around the circle’s center. As you do so, you’ll notice that the line divides the circle into two congruent (identical) halves.
This line of symmetry is just one of many. In fact, every diameter of a circle creates a new line of symmetry. This is because a circle is a perfectly round shape, which means that no matter which diameter you choose, it will always divide the circle into two identical parts.
So, how many lines of symmetry can a circle have? The answer is infinite. Because there are an infinite number of diameters that can be drawn through a circle’s center, there are also an infinite number of lines of symmetry. This makes the circle a unique and special shape in the world of geometry.
The Geometry of a Circle: Exploring Its Symmetry and More
There’s a fascinating world within the seemingly simple shape of a circle, teeming with mathematical intricacies and harmonious symmetries. Let’s embark on a geometrical journey to unravel the elegance of this captivating shape.
Understanding the Circle
A circle is the embodiment of perfect symmetry, a closed plane curve where all points lie equidistant from a fixed center point. Its radius is the distance from the center to any point on the circle, while its diameter is twice the radius, spanning across the circle’s widest point.
Properties of a Circle
Beyond its fundamental definition, a circle possesses several important properties:
- Circumference: The distance around the circle, measured by the formula 2πr, where π is the mathematical constant approximately equal to 3.14.
- Area: The space enclosed within the circle, calculated using the formula πr².
- Diameter and Circumference: The diameter is twice the length of the radius, and the circumference equals π times the diameter.
Symmetry and the Circle
The circle’s symmetry is a captivating aspect that defines its harmony. It is symmetrical around any diameter, meaning each diameter divides the circle into two congruent halves. This is because a circle is a rotational symmetry shape, identical under any rotation around its center.
But what makes the circle truly unique is its infinite lines of symmetry. Unlike regular polygons, where lines of symmetry are limited, a circle has an infinite number of diameters, each creating a new line of symmetry. This infinite symmetry creates a sense of endless harmonious repetition.
In essence, the geometry of a circle is a symphony of precision, symmetry, and mathematical intrigue. Its simple yet elegant form has captivated mathematicians, artists, and philosophers throughout history. It’s a shape that invites exploration and wonder, a testament to the beauty hidden within the abstract realms of geometry.