Understanding Terminal Points: Essential For Displacement Analysis

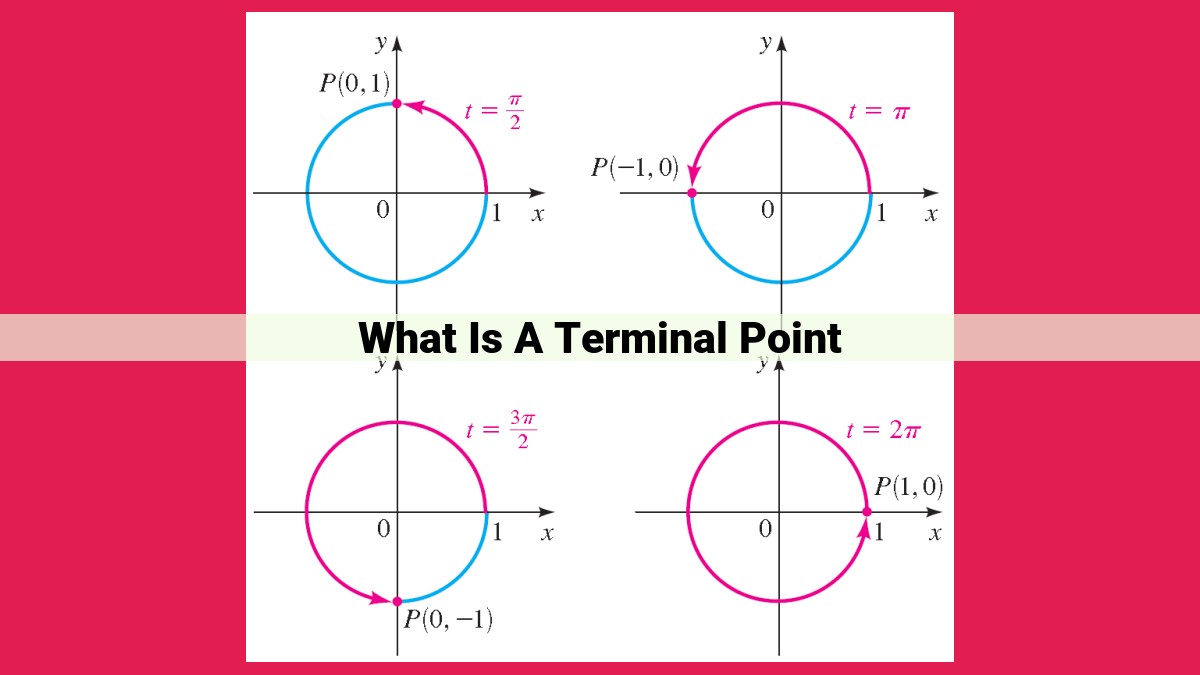
A terminal point is the endpoint of a directed line segment, indicating its direction. The initial point is the starting point of the line segment. The distance between the initial and terminal points determines the magnitude of the associated displacement vector, and the angle between the vector and the positive x-axis indicates its direction. Understanding terminal points is crucial for describing displacement, as they help determine the direction and magnitude of displacement vectors and are used in various fields such as physics and engineering.

Unveiling the Terminal Point: A Cornerstone of Displacement

In the realm of geometry and physics, terminal points play a pivotal role in defining and understanding directed line segments and displacement vectors. Embark on a journey to comprehend this fundamental concept and its significance in describing the motion of objects.

A terminal point is the endpoint of a directed line segment, which is a line segment that has a specified direction. It is crucial for designating the direction of a displacement vector, which is a quantity that describes both the magnitude and direction of an object’s displacement.

The initial point of a directed line segment is its starting point, while the terminal point is its endpoint. The distance between the initial and terminal points determines the magnitude of the displacement vector.

Thus, the terminal point serves as a crucial reference point for grasping the displacement of objects in space. It provides the necessary information to determine the direction and magnitude of such displacements, making it an indispensable tool in the fields of physics and engineering.

Related Concepts: Initial Point and Directed Line Segment

In the realm of displacement vectors, which play a pivotal role in describing the movement of objects in space, the terminal point takes center stage as the endpoint of these vectors. To grasp the concept of a terminal point, it’s essential to understand its two companion notions: the initial point and the directed line segment.

Picture a directed line segment as a path with a clear beginning and end, like an arrow with a tail and a head. The initial point serves as the starting point of this line segment, where the imaginary arrow begins its journey. Conversely, the terminal point marks the endpoint, where the arrow concludes its trajectory.

These two points work in tandem to define the direction of the displacement vector. The vector’s direction follows the path from the initial point to the terminal point, providing a sense of orientation for the vector. Imagine a river flowing from its source to its mouth. The source represents the initial point, and the mouth represents the terminal point, indicating the direction in which the water flows.

By understanding these concepts, we lay the groundwork for comprehending the intricate world of displacement vectors, which are indispensable in describing the motion of objects in our dynamic universe. So, next time you encounter a displacement vector, remember the crucial role played by its initial and terminal points, the guiding forces behind its direction.

Terminal Point and Displacement Vector

In the realm of physics and engineering, understanding the concept of terminal points is crucial for describing the displacement of objects in space. A terminal point, as the name suggests, is the endpoint of a directed line segment, and it plays a pivotal role in indicating the direction of a displacement vector.

A displacement vector, often represented as an arrow, is a mathematical representation of the change in position of an object. The direction of this vector is determined by the terminal point, while its magnitude is calculated by measuring the distance between the initial point (the starting point of the line segment) and the terminal point.

Terminal Point as the Endpoint of the Displacement Vector

The terminal point serves as the endpoint of the displacement vector, providing crucial information about the direction of the object’s movement. Imagine a projectile launched from point A and landing at point B. The displacement vector, represented by an arrow, would extend from point A to point B. The terminal point of this vector, at point B, would indicate the direction in which the projectile traveled.

Magnitude and Terminal Point

The distance between the initial point and the terminal point determines the magnitude of the displacement vector. This magnitude quantifies the extent of the object’s displacement, regardless of its direction. The magnitude can be interpreted as the length of the vector, providing a measure of the total change in position.

Understanding the concept of terminal points is essential for accurately describing the displacement of objects, whether it’s a projectile in motion or a force acting on an object. In physics and engineering, this knowledge is instrumental in analyzing and predicting the behavior of systems and objects in motion.

Terminal Points and Related Concepts in Understanding Displacement

In the realm of physics and mathematics, understanding terminal points is crucial for accurately describing the displacement of objects. A terminal point, simply put, is the endpoint of a directed line segment, a line segment with a specified direction. It plays a pivotal role in indicating the direction of a displacement vector, a mathematical representation of an object’s change in position.

The initial point of a directed line segment is its starting point, while the terminal point is its endpoint. The displacement vector is a vector that points from the initial point to the terminal point, and its magnitude, or length, represents the distance traveled by the object.

Other Related Concepts

To fully grasp the concept of terminal points, it’s essential to understand several related concepts:

• Magnitude: The magnitude of a displacement vector is its length, which corresponds to the distance traveled by the object.

• Direction: The direction of a displacement vector is the angle it makes with the positive x-axis. This angle specifies the direction in which the object has displaced.

• Unit Vector: A unit vector is a vector with a magnitude of 1 that points in a specific direction. It serves as a convenient way to represent the direction of a displacement vector.

Importance of Terminal Points in Describing Displacement

Terminal points are fundamental in describing displacement because they provide a precise way to quantify the direction and distance of an object’s movement. In physics and engineering, understanding terminal points is invaluable for:

• Modeling the motion of objects, such as projectiles, vehicles, and celestial bodies
• Calculating forces and torques acting on objects
• Designing navigation systems and control mechanisms
• Describing the flow of fluids and the behavior of waves

In summary, terminal points are vital for accurately characterizing the displacement of objects. By understanding their role in displacement vectors and related concepts like magnitude and direction, we can effectively describe and analyze the motion of objects in the physical world.

The Significance of Terminal Points in Describing Displacement

Understanding terminal points is crucial for comprehending the movement and displacement of objects in space. When we observe an object moving, we identify its starting position as the initial point and its ending position as the terminal point. This concept is fundamental in various fields, including physics and engineering.

The distance between the initial and terminal points determines the magnitude of the displacement vector, which represents the object’s overall change in position. The direction of the displacement vector is indicated by the angle between the vector and the positive x-axis. Terminal points play a vital role in defining this direction accurately.

For instance, in physics, the terminal point of a displacement vector represents the object’s final position after applying a specific force. Engineers use terminal points to design trajectories of projectiles, vehicles, and other systems. By understanding the relationship between the initial and terminal points and the displacement vector, engineers can optimize performance and ensure accurate movement.

In summary, terminal points are essential for describing displacement because they provide the necessary information about the object’s movement, including its magnitude and direction. This knowledge is indispensable in fields like physics and engineering, where accurate displacement measurements are crucial for problem-solving and system optimization.