Mastering Square Root Division For Enhanced Mathematical Proficiency
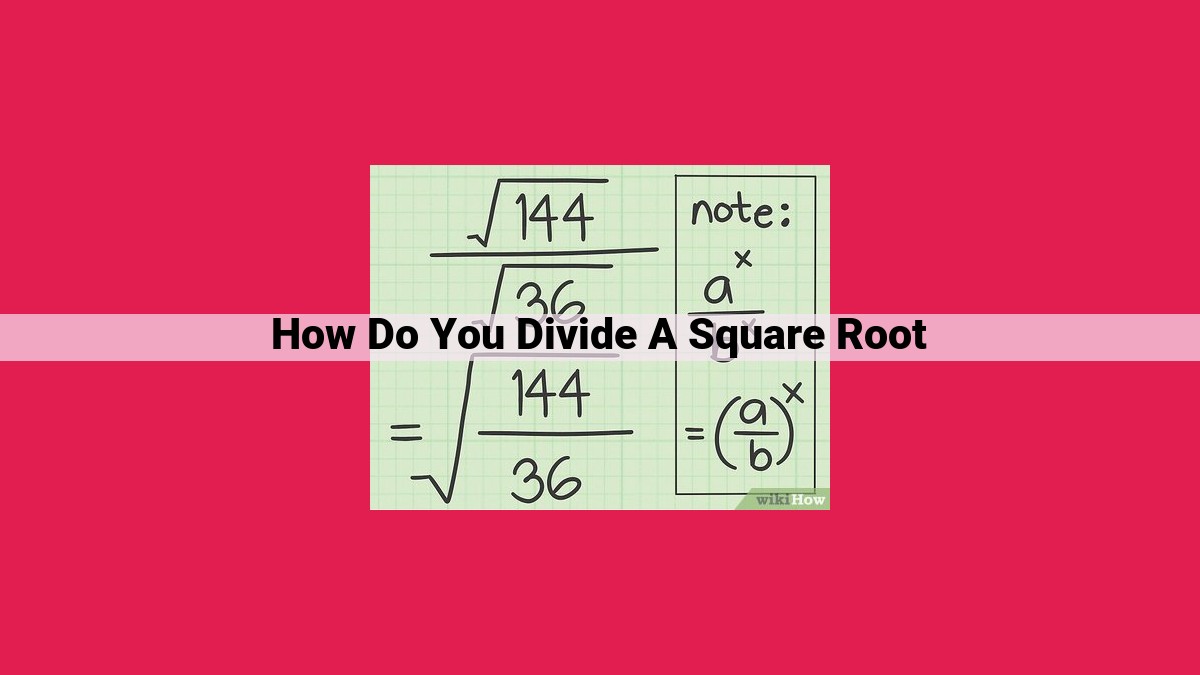
To divide a square root, use the rule √a ÷ √b = √(a ÷ b). Divide the numbers under the square root symbol before performing the square root operation. Understand that a square root represents the positive value of a number multiplied by itself. This concept is essential for mathematical understanding, as square roots appear in various equations, particularly quadratic equations, and are crucial in solving for unknown variables.
- Importance of understanding square roots in mathematical operations
- Necessity of dividing square roots for further mathematical understanding
Understanding the Essence of Dividing Square Roots: A Mathematical Journey
In the realm of mathematics, square roots hold a pivotal position. They serve as the key to unlocking numerous mathematical operations and concepts. But what happens when we encounter the need to divide square roots? This seemingly complex operation can be simplified by understanding a fundamental rule and its applications.
The Importance of Understanding Square Roots
Square roots are the inverse of squaring. They represent the value that, when multiplied by itself, gives the original number. Understanding square roots is crucial for various mathematical operations, including finding the area of squares and rectangles, calculating the distance between points on a plane, and solving quadratic equations.
The Necessity of Dividing Square Roots
As we delve deeper into mathematics, we encounter situations where dividing square roots is essential. It becomes necessary for solving more complex equations, simplifying algebraic expressions, and expanding our understanding of mathematical concepts. By mastering this skill, we unlock a gateway to further mathematical knowledge.
Understanding the Concept of Dividing Square Roots
The rule for dividing square roots is simple and straightforward:
√a ÷ √b = √(a ÷ b)
In other words, to divide two square roots, we simply divide the numbers inside the square root symbols. Let’s break down this rule step by step:
- Extract the numbers from the square root symbols: √a ÷ √b = a ÷ b
- Perform the division: a ÷ b
- Place the result inside a square root symbol: √(a ÷ b)
Related Concepts for Effective Application
To fully grasp the concept of dividing square roots, it’s essential to understand related concepts such as radicals and exponents. Radicals, represented by the √ symbol, denote the square root of a number. Exponents, on the other hand, represent the number of times a number is multiplied by itself. The connection between square roots and exponents is expressed as:
(√a)^2 = a
Additionally, square roots play a significant role in quadratic equations, which take the form of ax² + bx + c = 0. To solve these equations, we often need to find the square roots of the discriminant, which is calculated as b² – 4ac.
Example
Let’s demonstrate the rule of dividing square roots with an example:
√20 ÷ √5 = √(20 ÷ 5) = √4 = 2
This example illustrates how by applying the rule, we can simplify the division of square roots.
Dividing square roots is a fundamental concept in mathematics that opens up new possibilities for mathematical exploration. By understanding the rule, its application, and related concepts, we equip ourselves with the tools necessary for solving more complex problems and unlocking the beauty of mathematics.
Understanding the Concept of Square Root
Embark on a mathematical adventure as we delve into the captivating realm of square roots, a fundamental element that unlocks the complexities of mathematical operations.
Definition of a Square Root
A square root is a number that, when multiplied by itself, results in the original number. The square root of a number is often represented using the radical symbol √. For instance, the square root of 9 is written as √9 and equals 3, since 3 × 3 = 9.
Expressing Square Roots
The radical symbol, √, is commonly used to express square roots. For example, √16 represents the square root of 16, which is 4 (4 × 4 = 16). The number within the radical symbol is the radicand.
Practical Examples of Finding Square Roots
Let’s explore some real-world examples to grasp the essence of finding square roots:
-
To find the length of the diagonal of a square with sides of 5 units, we need to calculate the square root of the sum of the squares of the sides: √(5^2 + 5^2). This gives us a diagonal length of √(25 + 25) = √50.
-
The area of a circle is given by the formula πr^2, where r is the radius. To find the radius of a circle with an area of 49π, we need to divide the area by π and then take the square root: √(49π / π) = √49 = 7.
Dividing Square Roots: Unlocking Mathematical Simplicity
In the realm of mathematics, square roots hold a pivotal position. They allow us to unravel the secrets hidden within numbers, unlocking doors to complex equations. However, when faced with the task of dividing square roots, many may find themselves momentarily bewildered.
Fear not! This comprehensive guide will illuminate the path to mastering the art of dividing square roots. Its simple, step-by-step approach will empower you with the knowledge and confidence to conquer this mathematical enigma.
The Golden Rule: A Pathway to Clarity
The key to dividing square roots lies in understanding the fundamental rule:
√a ÷ √b = √(a ÷ b)
This rule serves as our guiding light, illuminating the path to success. Let’s break it down into bite-sized steps:
-
Extract the Numbers: Begin by extracting the numbers beneath the square root symbols. For example, if we are dividing √16 by √4, we extract 16 and 4.
-
Perform the Division: Divide the extracted numbers as you would any other numbers. In our example, 16 ÷ 4 = 4.
-
Place the Result Under the Radical Symbol: The result of the division becomes the number underneath the new square root symbol. In our case, the answer is √4.
That’s it! The process is as straightforward as slicing a pie. To ensure a thorough understanding, let’s delve into a practical example.
A Real-World Exploration
Consider the task of dividing √20 by √5. Following our golden rule, we extract the numbers (20 and 5) and perform the division (20 ÷ 5 = 4). Finally, we place the result under the radical symbol, yielding √4 as our answer.
In essence, dividing square roots involves breaking down the problem into manageable steps, applying our understanding of the rule, and embracing the power of simplicity. With practice and perseverance, you will master this mathematical skill and unlock the doors to a world of mathematical possibilities.
Dividing Square Roots: Simplifying Complexities
In the realm of mathematics, understanding square roots is paramount for navigating complex operations. Dividing square roots is a crucial step in unlocking further mathematical knowledge, empowering us to tackle more advanced concepts with ease.
Delving into Square Roots
A square root is essentially the inverse operation of squaring a number. It represents the value that, when multiplied by itself, gives the original number. Square roots are expressed using the radical symbol, √, with the number inside the radical indicating the number to be rooted. For instance, √9 = 3, as 3² = 9.
Dividing Square Roots: A Simple Rule
Dividing square roots follows a straightforward rule:
√a ÷ √b = √(a ÷ b)
This means that to divide the square root of a by the square root of b, we can simply find the square root of the division a by b.
Applying the Rule in Practice
Let’s illustrate this rule with an example: √20 ÷ √5. Using the rule, we have:
√20 ÷ √5 = √(20 ÷ 5) = √4 = 2
Related Concepts: Building a Foundation
To fully grasp the concept of dividing square roots, it’s essential to delve into related concepts:
– Radicals: Radicals represent the nth root of a number, where the square root is the second root (n = 2). For example, ∛64 = 4, as 4³ = 64.
– Exponents and Square Roots: Exponents indicate the number of times a base is multiplied by itself. The square root of a number can be expressed as a fractional exponent, where the denominator is 2. For instance, √16 = 16^(1/2).
– Square Roots in Quadratic Equations: Quadratic equations are equations of the form ax² + bx + c = 0, where the variable x is squared. The solutions to these equations often involve taking the square root.
Mastering the concept of dividing square roots is a fundamental step in mathematical understanding. By applying the simple rule and familiarizing ourselves with related concepts, we strengthen our mathematical foundation and empower ourselves to tackle more complex challenges. Remember, the key lies in embracing the simplicity and interconnections of mathematical concepts.
Dividing Square Roots: A Step-by-Step Guide to Mathematical Proficiency
Navigating the world of mathematics requires a firm grasp of square roots. They’re essential for unlocking the secrets of various mathematical operations. Understanding how to divide square roots is crucial for further mathematical comprehension.
Understanding Square Roots:
A square root is a number that, when multiplied by itself, gives you the original number. It’s represented using the radical symbol, √. For example, the square root of 25 is written as √25.
In practical terms, finding the square root of a number involves identifying the greatest perfect square that goes into the number. For instance, the greatest perfect square that goes into 25 is 16 (4 squared). Therefore, √25 = 4.
Dividing Square Roots:
Dividing square roots follows a simple rule:
√a ÷ √b = √(a ÷ b)
This means that to divide one square root by another, you simply divide the numbers inside the square roots.
Here’s a step-by-step explanation:
- Step 1: Write the division as a fraction of square roots: √a / √b
- Step 2: Apply the rule: √a / √b = √(a ÷ b)
- Step 3: Divide the numbers inside the square roots: √(a ÷ b)
Example:
Let’s say we want to divide √20 by √5.
- Step 1: √20 / √5
- Step 2: √(20 ÷ 5)
- Step 3: √4
Therefore, √20 ÷ √5 = √4 = 2
Related Concepts:
- Radicals: Square roots are expressed using radicals. The radical symbol, √, indicates the positive square root.
- Exponents: Square roots have a close relationship with exponents. For example, sqrt(x^2) = x.
- Quadratic Equations: Square roots play a vital role in solving quadratic equations of the form ax^2 + bx + c = 0.
Understanding how to divide square roots is a fundamental mathematical skill. By applying the rule and mastering related concepts, you’ll be well-equipped for more advanced mathematical endeavors. Remember, practice makes perfect, so don’t hesitate to work through examples and solidify your understanding.