Master The Art Of Solution Set Discovery: A Comprehensive Guide

To find solution sets, follow these steps:

• Define the problem and use set theory concepts like union, intersection, and complement to express it.
• Use interval notation to represent solutions on the number line or coordinate plane.
• Solve equations or inequalities to determine the set of values that satisfy the given conditions.
• Use methods like substitution, elimination, or graphing to find the solution set.

In the vast and wondrous realm of mathematics, a solution set emerges as a paramount concept, unveiling the secrets of equations and inequalities. It’s a treasure trove of all the values that satisfy a given mathematical statement, illuminating the hidden solutions that lie within its depths.

Solution sets are like maps that guide us through the labyrinth of equations, revealing the precise coordinates where truth resides. They allow us to pinpoint the exact numbers or variables that make a mathematical equation or inequality true. This knowledge empowers us to analyze, interpret, and solve a wide range of real-world problems, from calculating the optimal dosage of medicine to designing efficient transportation routes.

Imagine yourself as a detective tasked with solving a complex mystery. A solution set is your essential tool, narrowing down the myriad possibilities and leading you to the elusive truth. It’s the key that unlocks the door to understanding, giving you the power to decipher the hidden messages of mathematics.

Interval Notation: Unveiling the Secrets of Representing Solution Sets

In the realm of mathematics, solution sets are like hidden treasures, and interval notation is the key that unlocks their secrets. It’s a powerful tool that allows us to represent solution sets on the number line, providing a visual representation of the range of possible values.

Types of Intervals

Intervals come in various flavors, each with its unique characteristics:

• Open Intervals: These intervals span a range of numbers with no endpoints included. They are represented using parentheses, like (a, b).
• Closed Intervals: In contrast to open intervals, closed intervals include their endpoints. They are represented using brackets, like [a, b].
• Semi-open Intervals: Semi-open intervals have one closed endpoint and one open endpoint. They are represented using a combination of brackets and parentheses, like [a, b) or (a, b].
• Degenerate Intervals: Degenerate intervals have the same endpoint, which means they represent a single number. They are represented using square brackets, like [a, a].
• Disjoint Intervals: Disjoint intervals are sets of numbers that have no overlapping elements. They are represented using a union symbol, like (a, b) ∪ (c, d).

Representing Solution Sets

Interval notation allows us to represent solution sets in a concise and clear manner. For instance, if the solution set of an equation is all numbers greater than 5, it can be represented using the interval notation (5, ∞).

Using the Number Line

The number line provides a convenient visual representation of intervals. Open intervals are indicated by arrows at the endpoints, while closed intervals are indicated by solid lines at the endpoints. Degenerate intervals are represented by a single point on the number line.

Benefits of Interval Notation

Interval notation offers several advantages:

• Precision: It provides a precise and unambiguous way to represent solution sets.
• Succinctness: It allows complex solution sets to be expressed concisely.
• Visualization: It makes it easy to visualize the range of possible solutions on the number line.

Interval notation is an essential tool for representing solution sets in mathematics. By understanding the different types of intervals and how to use them on the number line, you’ll be able to unlock the secrets of solution sets and enhance your problem-solving abilities.

Set Theory: Uniting, Intersecting, and Excluding Sets

In the realm of mathematics, sets play a pivotal role in organizing and representing data. Set theory provides a framework for defining, manipulating, and visualizing sets, making it an essential tool for problem-solving and data analysis.

One of the fundamental concepts in set theory is the union of sets. The union of two sets A and B, denoted as A ∪ B, is the set that contains all elements that belong to either A or B or both. Imagine a Venn diagram where A and B are represented by overlapping circles. The union of A and B is the shaded region that encompasses both circles.

Another important operation is the intersection of sets. The intersection of two sets A and B, denoted as A ∩ B, is the set that contains all elements that belong to both A and B. Using the Venn diagram analogy, the intersection of A and B is the shaded region where the circles overlap.

Finally, the complement of a set A, denoted as A’, is the set that contains all elements that do not belong to A. To visualize the complement of A, simply shade the region outside the circle representing A in a Venn diagram.

To illustrate these concepts, consider the following example:

• A = {1, 2, 3}

• B = {2, 4, 5}

• A ∪ B = {1, 2, 3, 4, 5}

• A ∩ B = {2}
• A’ = {4, 5}

These set operations are essential for solving a variety of mathematical problems. They allow us to combine, subtract, and manipulate sets to obtain meaningful results.

Set Builder Notation: Expressing Sets Concisley

In the realm of mathematics, understanding solution sets is crucial for solving various equations and inequalities. Set Builder Notation provides an elegant way to express sets using curly braces and conditions, simplifying the representation of complex solution sets.

Imagine you’re facing an equation like x + 2 = 5. To find its solution set, you must identify all values of x that satisfy the equation. Using set builder notation, you can concisely represent this solution set:

{x | x + 2 = 5}

The curly braces, {, and }, signify a set. The vertical bar, |, means “such that”. And the expression inside the braces specifies the condition that must hold for the elements of the set. In this case, for x to belong to this set, it must have a value that makes x + 2 equal to 5.

Set builder notation becomes particularly useful when dealing with more complex conditions. For instance, to represent the solution set of the inequality 2x - 1 < 7, you can write:

{x | 2x - 1 < 7}

The curly braces encompass all the values of x that satisfy the condition 2x - 1 being less than 7.

Example: Express the set of all even numbers between 1 and 10 using set builder notation:

{x | x is an even integer and 1 < x < 10}

This notation clearly defines the set by specifying the conditions that its elements must meet. It simplifies the representation, avoiding the need to list all the individual elements.

Conclusion: Set Builder Notation is a powerful tool for expressing solution sets concisely. It enables you to define complex sets using conditions, making it easier to solve equations and inequalities and visualize the range of solutions. Whether you’re a student grappling with algebraic equations or a mathematician exploring advanced concepts, set builder notation is an essential tool for unraveling the mysteries of solution sets.

Solving Equations: A Guide to Finding Solutions

In the world of mathematics, finding solutions to equations is a crucial skill that unlocks the secrets of algebraic mysteries. An equation, represented by the iconic equal sign (=), sets two expressions on either side of the balance, inviting us to discover the values of unknown variables that tip the scales evenly.

To understand equations, we must first familiarize ourselves with variables. Think of variables as placeholders for unknown values, denoted by letters like x, y, and z. These variables represent numbers that we seek to uncover.

Expressions, on the other hand, are combinations of variables, numbers, and operations like addition, subtraction, multiplication, and division. They form the building blocks of equations. When we set two expressions equal to each other, we create an equation that challenges us to find the values of the variables that make the equation hold true.

There are various methods for solving equations, with substitution and elimination being two of the most common. Substitution involves isolating a variable in one expression and replacing it with its equivalent value in another expression. This technique is particularly effective when one variable is expressed in terms of other variables.

Elimination, on the other hand, involves manipulating the equations to cancel out variables or isolate them. This method often requires adding or subtracting multiples of one equation from the other to create equations with a single variable.

Solving equations is not just a mathematical exercise; it’s a problem-solving skill that finds applications in countless real-world scenarios. From calculating distances in physics to determining the profitability of a business, the ability to find solutions to equations empowers us to make informed decisions and unravel the complexities of our surroundings.

Solving Inequalities: A Practical Guide for Math Enthusiasts

Inequalities are an essential aspect of mathematics, extending the concept of equality to a broader range of relationships between numbers and expressions. Understanding how to solve inequalities is crucial for success in various fields, from science and engineering to economics and finance. This guide will delve into the world of inequalities, providing a comprehensive approach to solving them with confidence and clarity.

Defining Inequalities

An inequality is a mathematical statement that compares two expressions using symbols such as less than (<), greater than (>), less than or equal to (≤), and greater than or equal to (≥). Unlike equations that seek to find values that make the two sides equal, inequalities establish relationships that indicate one expression is either smaller or larger than the other.

Properties of Inequalities

1. Transitive Property: If a < b and b < c, then a < c.
2. Addition Property: If a < b, then a + c < b + c.
3. Multiplication Property: If a < b and c > 0, then ac < bc.
4. Multiplication Property (Negative): If a < b and c < 0, then ac > bc.

Solving Inequalities

Solving inequalities involves isolating the variable on one side of the inequality symbol while maintaining the original relationship. Similar techniques used in solving equations can be applied:

• Adding or Subtracting the Same Value: Add or subtract the same value to both sides of the inequality to maintain the inequality.
• Multiplying or Dividing by the Same Positive Value: Multiply or divide both sides of the inequality by the same positive value to preserve the inequality.
• Multiplying or Dividing by the Same Negative Value: If you multiply or divide both sides of an inequality by the same negative value, you must reverse the inequality symbol.

Example 1: Solve the inequality: x + 3 > 7

Solution: Subtracting 3 from both sides: x + 3 – 3 > 7 – 3, resulting in x > 4

Example 2: Solve the inequality: 2x – 5 ≤ 15

Solution: Adding 5 to both sides: 2x – 5 + 5 ≤ 15 + 5, resulting in 2x ≤ 20

Solving inequalities is a fundamental skill in mathematics, enabling us to analyze relationships between numbers and discover solutions to various problems. By understanding the definition, properties, and techniques for solving inequalities, you can approach any inequality with confidence and accuracy, expanding your mathematical prowess. So, embrace the challenges of inequalities and unlock the door to a deeper understanding of mathematical concepts!

Graphing Solutions: Visualizing Mathematical Solutions

Finding solution sets is a crucial aspect of mathematics, enabling us to determine which values satisfy a given equation or inequality. Graphing solutions provides a visual representation of these solutions, helping us understand their distribution and relationships.

Graphing Solutions for Equations

When graphing solutions for equations, we plot the points that fulfill the equation on a coordinate plane. For instance, to graph the equation y = 2x + 1, we would create a table of values for x, calculate the corresponding y values, and then plot the points (x, y) in the plane. The resulting graph is a linear line that represents all the points that satisfy the equation.

Graphing Solutions for Inequalities

Graphing solutions for inequalities involves a similar process, but with added attention to the type of inequality. For example, the inequality x > 2 represents all values of x greater than 2. To graph this inequality, we shade the region to the right of the line x = 2 on the number line. The resulting graph is a half-line, indicating that x can take any value greater than 2.

Interpreting Graphs

Graphs of solution sets offer valuable insights into the relationships between variables. By analyzing the shape, position, and intersections of these graphs, we can determine:

• The range of possible values for the variables
• Intersections between solution sets (indicating common solutions)
• Exclusions or restrictions on variable values (represented by shaded or empty regions)

Applications and Examples

Graphing solutions has practical applications in various fields, such as:

• Physics: Plotting trajectories of objects in motion
• Economics: Visualizing market trends
• Engineering: Designing optimal structures and systems

Graphing solutions is a powerful tool for visualizing and understanding solution sets. Using the number line and coordinate plane, we can represent solutions to equations and inequalities, analyze their relationships, and draw meaningful conclusions from the resulting graphs. This technique is essential for problem-solving, critical thinking, and making informed decisions based on mathematical models.

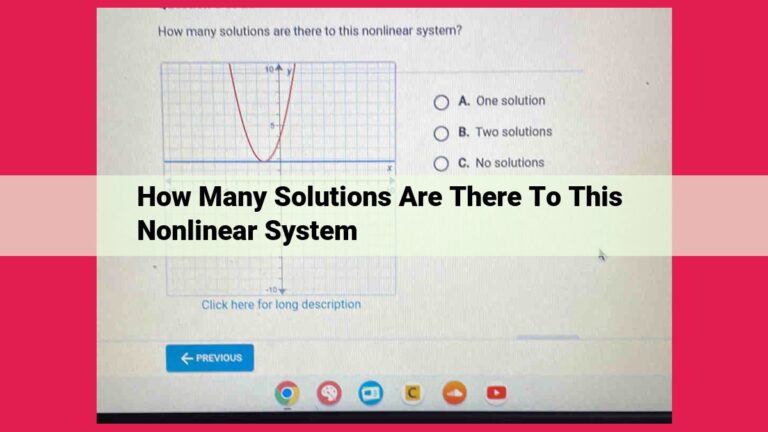
Systems of Equations and Inequalities: Unraveling the Interplay of Variables

In the realm of mathematics, solving systems of equations and inequalities takes us to the intersection of multiple unknowns. Just as a puzzle challenges our logical thinking, these systems present us with a set of interconnected equations or inequalities, each containing one or more variables.

Our mission is to find the solution set, a collection of values for the variables that satisfy all the given equations or inequalities simultaneously. To achieve this, we’ll delve into two powerful methods: elimination and substitution.

Elimination: The Art of Subtraction

The elimination method is a straightforward approach that involves adding or subtracting multiples of equations to create new equations that eliminate one or more variables. By carefully manipulating the equations, we can simplify the system until we’re left with equations that can be easily solved.

Substitution: Swapping Variables for Success

Alternatively, we can use the substitution method to isolate a variable in one equation and then replace it with its equivalent expression in the other equations or inequalities. This allows us to reduce the system to a smaller set of simpler equations that can be solved more directly.

Unveiling the Interplay

Systems of equations and inequalities arise in numerous real-life scenarios. For instance, economists might use them to model supply and demand relationships, while engineers employ them to calculate forces and stresses in complex structures. Understanding how to solve these systems is essential for navigating the intricate world of mathematics and beyond.

Harnessing Knowledge, Unlocking Solutions

So, fellow seekers of knowledge, let us embrace the challenge of solving systems of equations and inequalities. With a clear understanding of elimination and substitution, we can unlock the secrets of these mathematical puzzles and unravel the hidden relationships between variables.

Additional Tips for Enhanced Comprehension:

• Break down complex systems into smaller chunks.
• Practice regularly to improve your problem-solving abilities.
• Seek assistance from your instructor or a tutor if needed.
• Remember that patience and persistence are the keys to success.