Mastering Slope Relationships: Determining Perpendicular And Parallel Lines

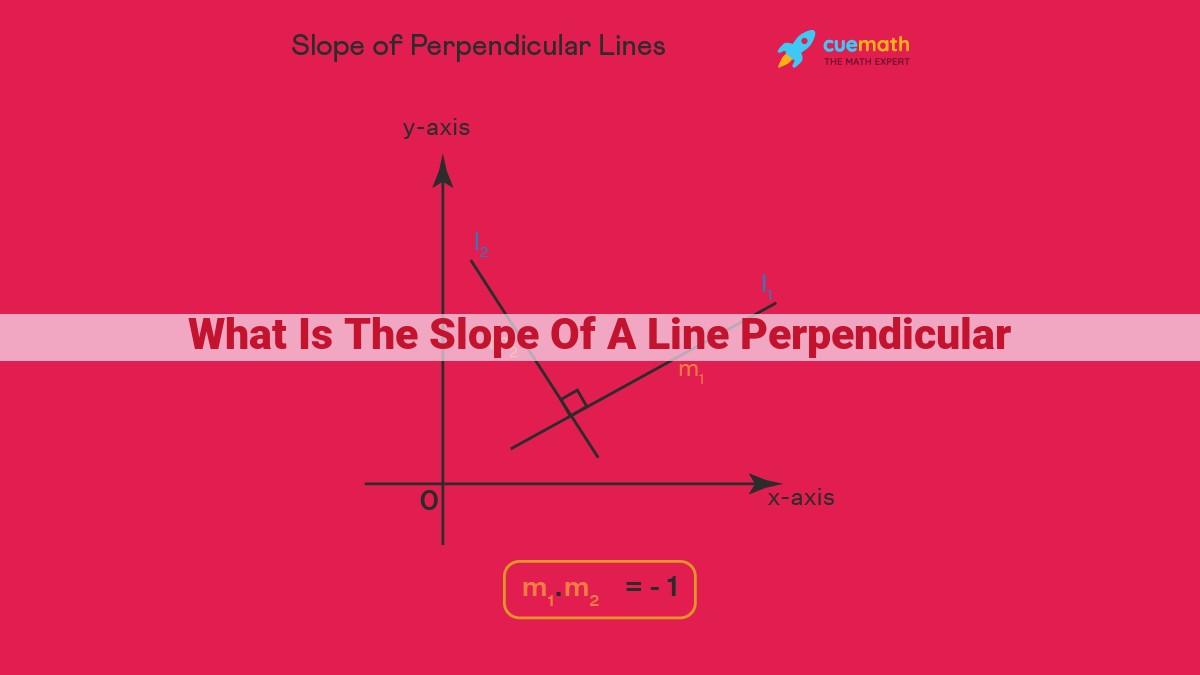
Understanding the concept of slope is crucial in determining the slope of a line perpendicular to another. Lines with slopes that are negative reciprocals of each other are perpendicular, meaning that their slopes are related by the formula -1/m, where m represents the slope of the first line. Lines that are parallel have the same slope, while those that are perpendicular have slopes that are negative reciprocals. Special cases arise with horizontal lines, which have a slope of 0, and vertical lines, which have an undefined slope.

Understanding the Concept of Slope: A Journey Through Lines

In the realm of geometry, lines dance across pages, revealing intricate patterns and relationships. One fundamental aspect of these lines is their slope, a measure that captures their ascent and descent. But what exactly is slope, and why is it so important?

The Essence of Slope: Rise Over Run

Imagine a line stretching across a graph. As it moves from one point to another, it either climbs or descends, tracing a path of change. Slope, in its purest form, quantifies this change by dividing the vertical distance traveled (the rise) by the horizontal distance traveled (the run).

The rise represents the change in the y-coordinate, while the run captures the change in the x-coordinate. Their ratio, the slope, provides a numerical representation of how steeply the line ascends or descends.

Deciphering Slope: A Window into Steepness

The magnitude of a slope tells us how steep a line is. A large positive slope indicates a line that is climbing rapidly, while a large negative slope suggests a line that is descending steeply. A slope of zero signifies a horizontal line, and an undefined slope characterizes a vertical line.

So, by understanding slope, we gain insight into the inclination of lines, unlocking their hidden geometry. It becomes a tool for describing the behavior of lines and predicting their future trajectories.

The Fascinating Relationship Between Perpendicular Slopes

When we talk about lines, one of the most important concepts to understand is slope. It measures the steepness of a line, telling us how much it rises or falls as we move along it. Now, let’s dive into a fascinating relationship that exists between perpendicular lines.

Perpendicular lines meet at a 90-degree angle, creating a right angle. Interestingly, these perpendicular lines have slopes that are negative reciprocals of each other. This means if we know the slope of one line, we can easily find the slope of its perpendicular.

Let’s suppose we have a line with a slope of m. The negative reciprocal of m is -1/m. So, if we draw a line perpendicular to this first line, its slope will be -1/m. This mathematical relationship is fundamental because it allows us to predict the slope of a perpendicular line without even seeing it.

This relationship is not only a neat mathematical fact but also has practical applications in real-world situations. For example, architects use it to ensure that buildings are structurally sound, while engineers rely on it when designing bridges and other structures. Understanding the relationship between perpendicular slopes is a cornerstone of geometry and essential for navigating our physical and mathematical worlds.

Distinguishing Parallel and Perpendicular Lines: A Geometric Tale

In the realm of geometry, lines dance gracefully across our imaginations, creating shapes, angles, and patterns that both intrigue and enlighten us. Among these lines, parallel lines and perpendicular lines possess unique relationships that reveal the hidden harmonies of our mathematical universe.

Parallel Lines: A Journey of Similarity

Picture two parallel lines, side by side, their paths unfolding side by side like two close friends. What unites these lines is their slope, a measure of their steepness, which remains identical. This shared slope symbolizes their unwavering similarity, like two peas in a pod. Parallel lines can waltz at any angle, whether gently sloping or steep as a mountain climb.

Perpendicular Lines: An Interplay of Opposites

Now, let’s shift our gaze to perpendicular lines, the perfect partners in crime. These lines stand in stark contrast to parallel lines, their paths crossing at right angles, forming a crisp 90-degree intersection. What connects these seemingly different lines is a fascinating mathematical dance. The slope of a perpendicular line is the negative reciprocal of the original line. In other words, if one line has a slope of 3, its perpendicular counterpart will have a slope of -1/3.

This intricate relationship between perpendicular lines highlights the balance and harmony that exists in the geometric realm. They complement each other perfectly, like yin and yang, their differences creating a whole that is greater than the sum of its parts.

Understanding the Concept of Slope

Imagine a roller coaster ride, where the track rises and falls as you move along. The slope of the track measures how steep it is, and it’s calculated by dividing the vertical change (the rise) by the horizontal change (the run). A steeper slope means the track rises or falls more quickly, while a flatter slope means it’s more gradual.

Relationship Between Perpendicular Slopes

Now, consider two roller coasters that cross each other like an X. Lines that are perpendicular to each other have a special relationship: their slopes are negative reciprocals of each other. This means that if one coaster has a slope of 2, the other coaster will have a slope of -1/2. It’s like a teeter-totter, where one side goes up when the other goes down.

Distinguishing Parallel and Perpendicular Lines

Lines can also be parallel or perpendicular. Parallel lines have the same slope, no matter what it is. Like two roller coasters running side by side, they never meet. Perpendicular lines, on the other hand, have slopes that are negative reciprocals, as we saw earlier. Just like the two coasters that cross each other, they intersect at a right angle.

Special Cases of Slope

What about lines that don’t go up or down at all?

• Horizontal Lines: These lines run parallel to the ground, like a flat track. They have a slope of 0, meaning they don’t change in height.
• Vertical Lines: These lines stand straight up, like a roller coaster track that’s going straight up or down. They have an undefined slope, because their run (horizontal change) is 0.

No matter what type of line you’re dealing with, understanding its slope can help you navigate the ups and downs of geometry like a pro!