How To Determine Slope Of Perpendicular Lines For Accuracy In Various Fields

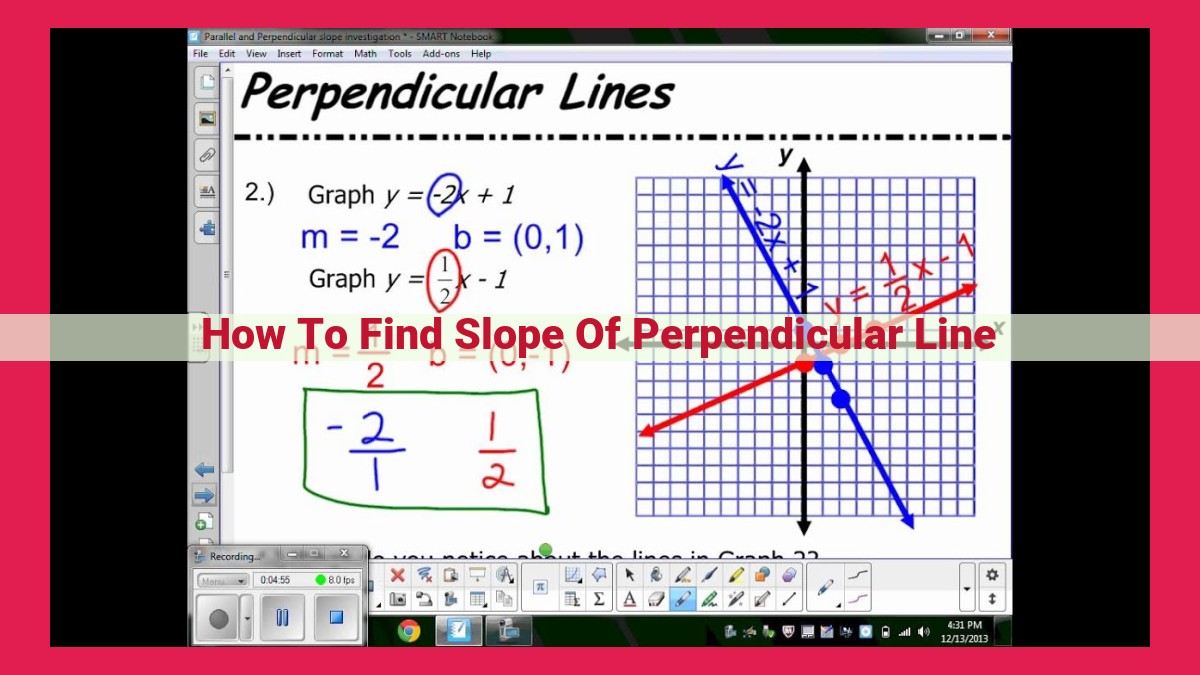
To find the slope of a perpendicular line, utilize the negative reciprocal method. Multiply the original slope by -1. Perpendicular lines intersect at right angles, meaning their slopes are negative reciprocals of each other. Understanding slopes involves the slope formula, expressed as Δy/Δx or y2-y1/x2-x1. This represents the change in vertical (Δy) divided by the change in horizontal (Δx) between two points. Perpendicular lines are crucial in various fields, ensuring accuracy and precision in construction, architecture, design, and problem-solving situations.

• Define perpendicular lines and their relationship to right angles.

Understand Perpendicular Lines and Their Significance in Geometry

In the world of geometry, lines that intersect at right angles are called perpendicular lines. These lines form a special relationship that has numerous applications in various fields.

Perpendicular lines are defined by their unique property of creating a 90-degree angle or a right angle where they meet. This characteristic is crucial in construction, architecture, design, and even problem-solving.

Understanding Slopes

Every non-vertical line has a property called slope, which describes its steepness. Slope is calculated using the slope formula, which involves the difference between the y-coordinates and the difference between the x-coordinates of two points on the line.

Slopes can be expressed in two forms:

• Slope-intercept form: y = mx + b, where m represents the slope
• Point-slope form: y – y1 = m(x – x1), where m is the slope and (x1, y1) is a point on the line

Finding the Slope of a Perpendicular Line

If two lines are perpendicular, their slopes have a specific relationship. The slope of a perpendicular line is the negative reciprocal of the original line’s slope. This means that if the original line has a slope of m, then the slope of the perpendicular line will be -1/m.

This negative reciprocal method provides a straightforward way to calculate the slope of a perpendicular line without performing any complex calculations.

Understanding Slopes: The Gateway to Perpendicularity

To unravel the secrets of perpendicular lines, we must first delve into the world of slopes. A slope, often denoted by the letter “m,” is a mathematical concept that describes the steepness and direction of a line. It tells us how much a line “rises” or “falls” as we move along its length.

The slope formula, the cornerstone of slope calculation, is given by:
m = (y2 - y1) / (x2 - x1)

Where (x1, y1) and (x2, y2) are two distinct points on the line.

The slope-intercept form of a linear equation, expressed as y = mx + b, is particularly useful because it explicitly reveals the slope as the coefficient of the x variable. The constant term b represents the y-intercept, the point where the line crosses the y-axis.

Another common representation is the point-slope form: y - y1 = m(x - x1). This form is particularly handy when given a single point and the slope of the line.

Finding the Slope of a Perpendicular Line: A Negative Reciprocal Approach

In the realm of geometry, perpendicular lines hold a special significance, forming right angles that are indispensable for a myriad of applications. Understanding how to determine the slope of a line perpendicular to another is crucial in various fields, from construction to design.

The concept of slope, measured as the ratio of vertical to horizontal change, plays a central role in describing the steepness of a line. When dealing with perpendicular lines, however, a remarkable relationship exists: their slopes are negative reciprocals of each other.

To grasp this principle, consider a line with slope m. Its perpendicular partner will have a slope of -1/m. This means that the negative reciprocal of the original slope gives us the slope of the perpendicular line. Let’s break it down:

• If the original slope is positive, its perpendicular counterpart will have a negative slope.
• If the original slope is negative, its perpendicular will have a positive slope.
• If the original slope is zero (a horizontal line), its perpendicular will be vertical with an undefined slope (-∞).
• If the original slope is undefined (a vertical line), its perpendicular will be horizontal with a slope of 0.

This negative reciprocal relationship is a useful tool in various situations. For instance, in architecture, ensuring that walls are perpendicular to the ground (sloped roofs) or to each other (adjacent walls meeting at right angles) requires precise knowledge of slopes. Similarly, in construction, determining the angle of a support beam relative to the ground or other structural elements relies on calculating perpendicular slopes.

Examples in Action

To solidify our understanding, let’s explore some examples:

• If a line has a slope of 2, its perpendicular line will have a slope of -1/2.
• If a line is vertical (undefined slope), its perpendicular line will be horizontal with a slope of 0.
• If a line has a slope of -3, its perpendicular line will have a slope of 1/3.

Mastering the concept of calculating the slope of a perpendicular line using the negative reciprocal method is a geometric skill with far-reaching applications. Whether in construction, architecture, design, or problem-solving, the ability to determine perpendicular slopes empowers us to create precise and functional structures, solve geometric puzzles, and tackle real-world challenges with confidence.

Applications of Perpendicular Lines: Building a World of Precision and Harmony

Perpendicular lines are the cornerstones of countless human endeavors, from architecture and construction to design and problem-solving. They provide a solid foundation for structural stability, aesthetic beauty, and functional efficiency.

In construction, perpendicular lines ensure that walls, roofs, and frameworks stand tall and strong. They guide structural beams and trusses to create load-bearing skeletons that can withstand the test of time. Without perpendicularity, buildings would crumble and towers would sway, jeopardizing both life and property.

Architecture owes its beauty and elegance to the precise placement of perpendicular lines. In classic columns, soaring cathedrals, and modern skyscrapers, perpendicular lines define symmetry, balance, and proportion. They create a sense of order and harmony that is pleasing to the eye and inspires awe in the beholder.

Design is another realm where perpendicular lines play a pivotal role. From the layout of cities to the aesthetics of furniture, perpendicularity brings a sense of organization and clarity. Intersecting lines create grids and patterns that guide the flow of movement, connect spaces, and enhance visual appeal.

Beyond aesthetics, perpendicular lines serve as indispensable tools in problem-solving. They aid in navigation, surveying, and engineering by providing a reference point and directional guidance. By establishing perpendicular lines, we can determine distances, measure angles, and solve complex geometrical puzzles.

In the grand tapestry of human innovation, perpendicular lines are threads that weave together stability, beauty, and functionality. From the towering skyscrapers that grace our cities to the intricate designs that adorn our homes, perpendicular lines are the invisible forces that shape our world and make it a more livable, aesthetically pleasing place.

Finding the Slope of a Perpendicular Line: A Practical Guide

In the world of geometry, lines often intersect, forming angles and creating unique relationships. Two intersecting lines are considered perpendicular when they form a 90-degree (right) angle. Understanding the relationship between perpendicular lines and their slopes is crucial in various fields, including construction, architecture, and design. This article will delve into the concept of perpendicular lines and provide a step-by-step guide to calculating the slope of a perpendicular line based on a given original line.

Understanding Slopes

Every line has a slope, which describes its steepness and direction. It is calculated by dividing the change in the y-coordinate by the change in the x-coordinate between two points on the line. The slope formula is:

m = (y2 - y1) / (x2 - x1)

where (x1, y1) and (x2, y2) are the coordinates of two points on the line.

Finding the Slope of a Perpendicular Line

A fascinating property of perpendicular lines is that their slopes have a specific mathematical relationship. The slope of a line perpendicular to another line is the negative reciprocal of the original slope. In other words, if the original line has a slope of m, the slope of the perpendicular line will be -1/m.

m_⊥ = -1/m

where m_⊥ is the slope of the perpendicular line and m is the slope of the original line.

Examples

Let’s illustrate this concept with some examples:

• Example 1:

  If a line has a slope of 2, the slope of the perpendicular line would be:

  m_⊥ = -1/2
  

• Example 2:

  If another line has a slope of -3/4, the slope of the perpendicular line would be:

  m_⊥ = -1/(-3/4) = 4/3
  

Applications of Perpendicular Lines

The concept of perpendicular lines has numerous practical applications:

• Construction: Ensuring that walls, beams, and other structural elements are perpendicular to each other creates stability and prevents structural failures.
• Architecture: Perpendicular lines are used to create aesthetically pleasing designs, such as in the placement of columns, windows, and doors.
• Design: Perpendicular lines can create balance and symmetry in graphic design, web design, and typography.
• Problem-Solving: Finding the slope of a perpendicular line can help solve geometry problems involving perpendicularity, angles, and distances.

Understanding perpendicular lines and their slopes is not only a mathematical concept but also a practical tool with applications in various fields. By following these steps, you can confidently calculate the slope of a perpendicular line and utilize this knowledge to enhance your problem-solving abilities and achieve greater precision in design and construction projects.