Understanding Slope: A Key Concept In Geometry And Data Analysis

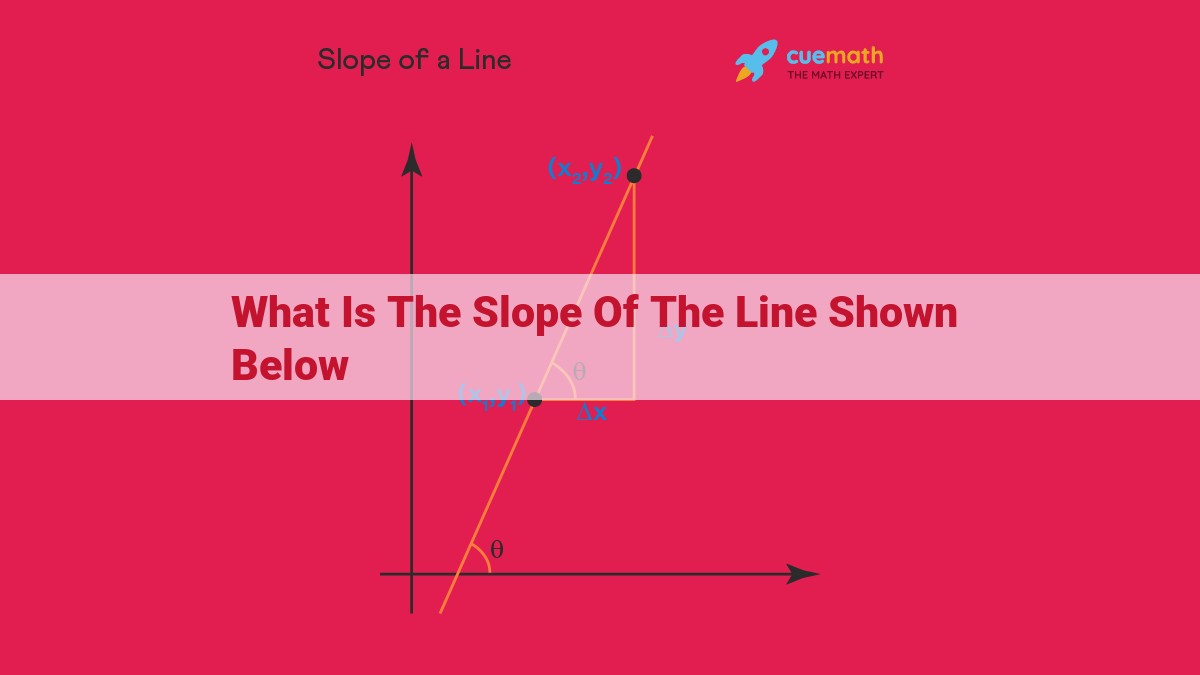
The slope of a line is a mathematical concept that describes its steepness and direction. It is calculated as the ratio of the vertical change (“rise”) to the horizontal change (“run”) between any two points on the line. The slope indicates the rate of change along the line, with a positive slope indicating a line that slopes upward from left to right, and a negative slope indicating a line that slopes downward from left to right. Understanding slope is essential in geometry and its applications, as it allows for the analysis of patterns, relationships, and trends within data.

In the realm of geometry, where shapes and lines intertwine, understanding slope is like having a secret key to unlocking the secrets of lines. It’s a concept that not only fascinates mathematicians but also plays a pivotal role in diverse fields, from architecture to economics.

So, what exactly is slope? It’s the measure of the inclination or slant of a line, a numerical value that quantifies how much the line rises or falls as you move along its length. It’s the “rise over run” that describes the steepness of the line, telling us how much the y-coordinate (the “rise”) changes for every unit change in the x-coordinate (the “run”).

Understanding the Language of Slope

Slope is often accompanied by a colorful vocabulary that adds depth to its description:

• Gradient: Another term for slope, highlighting its role in describing the rate of change.
• Incline: The angle of elevation or descent, measured from the horizontal plane.
• Steepness: A qualitative description of the slope’s magnitude, indicating how sharply the line rises or falls.

Calculating the Elusive Slope

Finding the slope of a line is a straightforward calculation. Using the ‘rise over run’ formula, we determine:

Slope = Δy / Δx

where Δy represents the rise (change in y-coordinate) and Δx represents the run (change in x-coordinate) between two points on the line.

Additional Considerations

Along with the slope, there’s another key aspect to consider: the y-intercept. It’s the point where the line crosses the y-axis, and it tells us the initial value of the line. The slope and y-intercept together fully define a linear equation, allowing us to precisely describe the line’s behavior.

Understanding Slope Terminology

In the realm of geometry, slope is a fundamental concept that describes the slant or steepness of a line. It provides valuable insights into the line’s behavior and has myriad applications in various fields. To delve deeper into slope, it’s crucial to understand the related terminology.

One such term is gradient, which is synonymous with slope. It denotes the rate of change between two points on a line. Incline refers to the angle formed between a line and the horizontal axis, conveying the line’s upward or downward slant.

Steepness is a qualitative measure of a line’s slope, indicating how quickly or gradually it changes. A line with a steeper slope is more inclined than one with a gentler slope. Rate of change is a quantitative measure of the line’s slope, which is calculated as the difference in y-coordinates divided by the difference in x-coordinates between two points on the line.

Calculating Slope: A Journey through the Heart of Lines

In the boundless realm of geometry, lines possess a captivating property called slope. It’s like a heartbeat, revealing the line’s trajectory and its angle of inclination. Understanding how to calculate slope unlocks a treasure trove of insights into the behavior of these geometric entities.

The Formula Unveiled: Rise Over Run

The formula for calculating slope is a simple yet elegant equation:

Slope = ** **(Change in y) / (Change in x)

This formula captures the line’s rise, or vertical change, and its run, or horizontal change. By dividing the rise by the run, we obtain a numerical value that represents the line’s slope.

An Illustrative Example

Let’s imagine a line passing through the points (2, 5) and (6, 11). To calculate its slope, we first determine the rise and run:

• Rise: (11 – 5) = 6 (The y-coordinate changes by 6 units.)
• Run: (6 – 2) = 4 (The x-coordinate changes by 4 units.)

Now, we apply the formula:

Slope = 6 / 4 = ** **3/2

So, the slope of the line passing through (2, 5) and (6, 11) is 3/2. This means that for every 2 units the line moves horizontally, it rises by 3 units vertically.

Calculating slope is a fundamental skill in geometry that empowers us to decipher the secrets of lines. Whether you’re an architecture student designing a building or an economist analyzing market trends, grasping the concept of slope will illuminate your path and enhance your understanding of the geometric world around you.

Additional Considerations:

Delving deeper into the world of slope, let’s explore some additional aspects that illuminate its significance. One key concept to grasp is the y-intercept. This point represents where the line crosses the y-axis, indicating the line’s starting value. The y-intercept plays a crucial role in understanding the overall behavior of the line.

For instance, imagine you’re analyzing a line representing the temperature change over time. The y-intercept of this line would tell you the initial temperature at the beginning of the time period being considered. By understanding the y-intercept, you gain valuable insights into the context of the line’s slope.

In addition to the standard slope formula, there are alternative methods to determine slope that can be equally useful. The slope-intercept form of an equation is a convenient way to represent a line by expressing it in terms of slope and y-intercept. This form takes the shape of:

y = mx + b

Here, m represents the slope, and b represents the y-intercept. By manipulating this equation, you can easily calculate the slope by solving for m. The slope-intercept form is particularly helpful when working with lines that have a non-zero y-intercept.

Understanding the intricacies of slope, y-intercept, and alternative slope calculation methods empowers you with a comprehensive toolkit for analyzing and interpreting lines. These concepts are fundamental to various fields, providing a solid foundation for decision-making and problem-solving.

Slope: A Key Concept in Geometry and Beyond

Understanding slope is essential for comprehending the behavior of lines in geometry. However, its significance extends far beyond the classroom, with practical applications in fields such as architecture, engineering, and economics.

In architecture, slope plays a crucial role in designing buildings and structures. For example, architects consider the slope of ramps and stairs to ensure that they are accessible and safe for users. Similarly, in engineering, slope is used to calculate the incline of bridges and roadways, ensuring their stability and efficiency.

Slope also finds its place in economics. The demand curve is a line that illustrates the relationship between price and quantity demanded for a good or service. The slope of the demand curve indicates how much the quantity demanded changes in response to a change in price. Understanding the slope allows economists to make predictions about consumer behavior and market dynamics.

Additionally, slope is used in statistics to analyze data and identify trends. By calculating the slope of a regression line, researchers can determine the linear relationship between two or more variables. This information is valuable for making forecasts and assessing the impact of one variable on another.

For instance, in a study that investigates the relationship between study hours and exam grades, the slope of the regression line would indicate how much the exam grade increases for each additional hour of study. This knowledge helps students optimize their study time and predict their potential performance in exams.

Overall, understanding slope is essential for a wide range of disciplines, from engineering to economics to data analysis. It provides valuable insights into the behavior of lines and enables professionals to make informed decisions and predictions based on real-world data.

**Factors that Shape the Slope of a Line**

The slope of a line, a critical concept in geometry, is influenced by several intriguing factors that we will explore in this section.

Firstly, the coordinates of the points that define the line play a pivotal role in determining its slope. The slope is calculated as the rise (vertical change) over the run (horizontal change) between any two points on the line. By altering the coordinates of these points, you can effectively alter the slope of the line.

For instance, if you increase the vertical distance (rise) between the points while keeping the horizontal distance (run) constant, the slope of the line will become steeper. Conversely, if you decrease the vertical distance while maintaining the same horizontal distance, the slope will become less steep. Similarly, changing the horizontal distance while keeping the vertical distance constant will impact the slope.

Another factor that influences slope is the orientation of the line in the coordinate plane. A positive slope indicates a line that moves upward from left to right, while a negative slope denotes a line that descends from left to right. The magnitude of the slope determines how pronounced the upward or downward movement is.

Lastly, the slope of a line can be affected by a transformation such as translation, rotation, or reflection. These transformations can alter the coordinates of the points on the line, thereby changing its slope. However, it’s important to note that transformations like translation, which move the line up, down, left, or right without altering its shape, do not affect its slope.

Understanding these factors not only enhances our comprehension of slope but also empowers us to manipulate lines and analyze their behavior effectively. Whether in architecture, engineering, or economics, the concept of slope plays a pivotal role in problem-solving and making informed decisions.