Discover Slope Field Techniques: Visualize Differential Equation Solutions

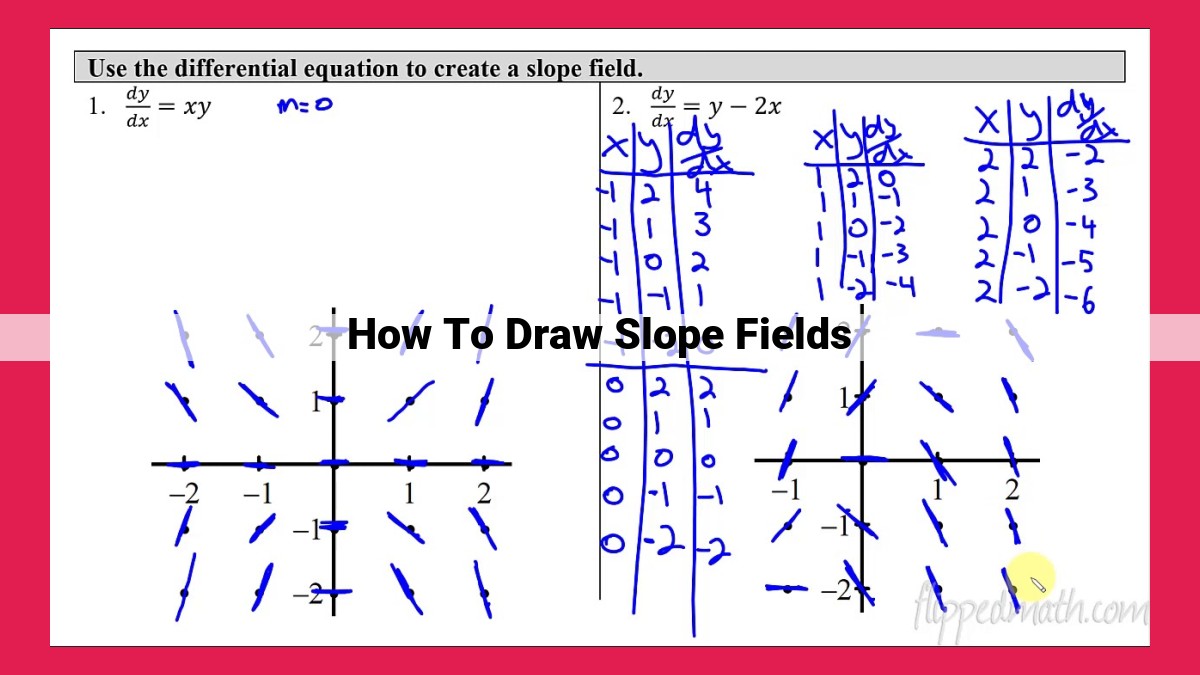
To draw slope fields for differential equations, follow these steps: 1) Plot points in the x-y plane; 2) At each point, calculate the slope using the given equation; 3) Draw a short line segment with the calculated slope at each point; 4) Connect the line segments to create a visual representation of the solution curves. This graphical tool helps analyze the behavior of differential equations, identifying critical points, nodal lines, and stable or unstable equilibrium points.

Slope Fields: Unveiling the Dynamics of Differential Equations Visually

Delve into the fascinating world of differential equations, where slope fields emerge as a powerful visual tool. They transform complex equations into vibrant landscapes, allowing us to graphically analyze their solutions and gain invaluable insights into the underlying system’s behavior.

Slope fields are like roadmaps, guiding us through the slope of a differential equation at each point. By connecting these slopes, we create a tapestry of arrows that reveal the direction of change for the dependent variable as the independent variable varies. This graphical representation is a powerful tool for understanding the dynamic behavior of the system described by the equation.

Imagine a physicist studying the trajectory of a projectile, or an engineer analyzing the flow of a fluid. Slope fields provide them with a visual representation of the system’s evolution over time. By observing the slopes, they can identify regions where the system is stable, unstable, or exhibits complex behavior. This knowledge is crucial for predicting future outcomes and making informed decisions.

Moreover, slope fields enable us to identify critical points, where the slope is zero. These points represent equilibrium states, where the system is neither changing nor moving away from its current position. Understanding the location and stability of critical points is essential for unraveling the dynamics of the system.

By combining slope fields with eigenvalues and eigenvectors, we gain an even deeper understanding of system behavior. Eigenvalues quantify the stability and rate of change at critical points, while eigenvectors indicate the direction of change. This knowledge empowers us to classify critical points as stable, unstable, or saddle points.

In ecology, slope fields are used to model the population dynamics of interacting species. They visualize the competition, cooperation, and predator-prey relationships, providing ecologists with valuable insights into the stability and resilience of ecosystems.

In conclusion, slope fields are an invaluable tool that brings differential equations to life. They transform complex equations into visual representations, making them accessible and intuitive. By harnessing the power of slope fields, scientists, engineers, and researchers gain a deeper understanding of the dynamics and behavior of the systems they study.

Drawing Slope Fields: A Visual Guide

Embark on a journey into the captivating world of differential equations, where slope fields emerge as powerful tools to unravel their intricacies. A slope field is a visual representation that unveils the behavior of differential equations, allowing us to gain insights into the dynamics of complex systems.

To embark on this artistic adventure, we must first master the art of drawing slope fields. Follow these steps like a skilled cartographer:

1. Identify the Differential Equation: The equation y’ = f(x, y) guides our path. It tells us how the slope of the solution curves changes with respect to x and y.

2. Choose a Grid: Divide the desired region into a grid of points. These points will serve as our exploration sites.

3. Calculate Slopes: At each grid point, we calculate the slope using the differential equation. This slope represents the direction of the tangent line to the solution curve at that point.

4. Draw Arrows: Armed with the slopes, we draw short arrows at each grid point. These arrows point in the direction of the slope, guiding us toward the path of the solution curves.

As we delve deeper into slope fields, we encounter two closely related concepts:

• Direction field: A synonym for slope field. It emphasizes the directional aspect of the field.

• Slope: The tangent of the angle made by the tangent line with the horizontal axis. It quantifies the rate of change of the solution curve.

Critical Points: Unlocking the Secrets of Equilibrium in Differential Equations

In the realm of differential equations, critical points emerge as pivotal elements, holding the key to understanding the behavior and stability of a system. These points, where the slope field intersects the x-axis or y-axis, serve as equilibrium points, representing states where the rate of change is zero.

To delve into the significance of critical points, let’s embark on a journey into the world of differential equations. Differential equations describe the rate of change of a variable over time. By studying the slope field of a differential equation, which graphically depicts the slope of its solutions at every point in the plane, we can gain valuable insights into the behavior of the system.

Critical points arise when the slope of the solution becomes zero. At these points, the system reaches an equilibrium state, where no further change occurs. Understanding the location and nature of critical points is crucial for analyzing the stability and dynamics of the system.

By identifying critical points, we can determine whether the system will tend towards stability or instability. Stable equilibrium points, for example, represent states where the system will return to its equilibrium after a perturbation. On the other hand, unstable equilibrium points indicate states where any perturbation will cause the system to move away from equilibrium.

To fully grasp the importance of critical points, consider a simple differential equation that models the growth of a population. The slope field for this equation depicts the rate of change of the population over time. By identifying the critical point where the slope is zero, we can determine the equilibrium population level. This knowledge allows us to predict the long-term behavior of the population under different conditions.

In conclusion, critical points are essential landmarks in the landscape of differential equations. They provide valuable insights into the equilibrium states of a system and enable us to understand its stability and dynamics. By identifying and analyzing critical points, we unlock the secrets of differential equations and gain a deeper understanding of the systems they describe.

Nodal Lines: Unraveling the Secrets of Stability in Differential Equations

In the realm of differential equations, slope fields provide a visual gateway to unraveling the intricate dynamics of a system. They are like a roadmap, guiding us through the labyrinth of solutions and illuminating the hidden patterns that govern the system’s behavior. And within this vibrant tapestry of slope fields, there exists a special type of line that holds great significance: the nodal line.

A nodal line is a curve in the slope field where the slope is zero. This means that at any point along a nodal line, the solution to the differential equation has no directional bias. The system is in a state of equilibrium, neither moving in one direction nor the other.

Nodal lines play a crucial role in determining the overall stability of a system. They divide the slope field into regions where the solutions behave differently. On one side of a nodal line, the solutions may flow towards a critical point, indicating stability. On the other side, solutions may flow away from the critical point, signaling instability.

Identifying nodal lines from a slope field is a valuable skill. They can be found by looking for curves where the slope is zero or where the slope changes sign. Nodal lines can also be identified by using a nullcline analysis, where the differential equation is set to zero.

Understanding the significance of nodal lines is essential for comprehending the dynamics of differential equations. They provide insights into the system’s equilibrium points and its overall stability, shaping the trajectory of solutions and revealing the hidden forces that govern the system’s behavior.

Saddle Points: Points of Instability

In the realm of differential equations, saddle points stand out as intriguing points where the system’s behavior takes on a dynamic and unpredictable nature. These points, aptly named for their resemblance to the shape of a saddle, are characterized by eigenvalues with opposite signs.

Imagine a slope field depicting the behavior of a differential equation. At a saddle point, the slopes of the curves intersect like the ridges of a saddle, forming a separatrix. This separatrix divides the plane into regions where solutions either converge or diverge from the saddle point.

The presence of a saddle point indicates instability. Solutions approaching the saddle point from one side will tend to spiral away, while those approaching from the other side will be drawn towards it. This behavior is due to the opposing forces acting on the system, causing it to oscillate indefinitely around the saddle point.

Saddle points play a crucial role in understanding the dynamics of systems. They can represent points of bifurcation, where small changes in the system’s initial conditions can lead to dramatically different outcomes. Identifying and analyzing saddle points is therefore essential in fields such as physics, engineering, and ecology, where predicting the behavior of complex systems is paramount.

Stable Equilibrium Points: The Pillars of Stability

In our exploration of differential equations, we delve into the realm of stability, where critical points play a pivotal role. Among these critical points, stable equilibrium points stand out as the guardians of convergence, the points towards which solutions perpetually drift.

Definition and Graphical Representation of Stable Equilibrium Points

Mathematically, a stable equilibrium point is a point where the eigenvalues of the system’s Jacobian matrix are both negative. This means that infinitesimally close solutions to the differential equation will converge towards the equilibrium point as time progresses.

Graphically, stable equilibrium points are depicted as points where the slope field flows inward towards the point. This inward flow symbolizes the tendency of solutions to approach the equilibrium point. Consider a phase portrait, a visual representation of the system’s behavior, where the slope field originates from the equilibrium point. The trajectories, or flow lines, resemble inward spirals, indicating the convergence of solutions towards the stable equilibrium point.

Identifying Stable Equilibrium Points from the Slope Field

Identifying stable equilibrium points from the slope field is crucial for understanding the system’s dynamics. Look for points where the slope field flows inward towards a particular point. This inward flow is a visual cue that the point is a stable equilibrium point. Alternatively, the slope field can be used to sketch the phase portrait, where the inward spirals will reveal the stable equilibrium points.

Role of Stable Equilibrium Points in System Stability

Stable equilibrium points play a pivotal role in the stability of a system described by differential equations. Solutions starting near a stable equilibrium point will remain close to it over time, even in the presence of small disturbances. This stability is due to the negative eigenvalues, which dictate that solutions will converge towards the equilibrium point.

Stable equilibrium points represent asymptotically stable systems, where solutions approach the equilibrium point as time approaches infinity. This stability is crucial in modeling real-world phenomena, such as the equilibrium of a spring-mass system or the stability of a population in ecology.

In summary, stable equilibrium points are critical points where solutions converge due to the negative eigenvalues of the system’s Jacobian matrix. They are graphically represented by inward-flowing slope fields and are associated with asymptotic stability. Identifying and analyzing stable equilibrium points is essential for understanding the dynamics and stability of differential equations.

Unstable Equilibrium Points: Points of Divergence

In the realm of differential equations, equilibrium points mark the moments of balance within a system. However, not all equilibrium points are created equal. Some, known as stable equilibrium points, are like tranquil lakes where solutions gently settle and remain. Others, called unstable equilibrium points, resemble precarious cliffs from which solutions are destined to tumble away.

Unstable equilibrium points arise when both eigenvalues of the system are positive. These positive eigenvalues indicate that the system has an inherent drive to escape from the equilibrium point. Imagine a ball balanced at the top of a hill. The slightest perturbation will send the ball rolling down the hill, away from the unstable equilibrium point.

Graphically, unstable equilibrium points are represented by slope fields that point away from the equilibrium point. These slope fields visually convey the system’s tendency to diverge from the equilibrium state. As solutions approach the unstable equilibrium point, their trajectories curve away, indicating the system’s relentless push to move further away.

Identifying unstable equilibrium points from a slope field is crucial for understanding the dynamics of the system. They represent points of potential instability, where solutions are perpetually poised to depart from equilibrium. These unstable points can heavily influence the system’s behavior, dictating whether solutions converge to other equilibrium points or diverge indefinitely.

Unstable equilibrium points find applications in various fields, including physics, engineering, and ecology. They can model phenomena such as radioactive decay, unstable chemical reactions, and the dynamics of predator-prey relationships. Understanding unstable equilibrium points, therefore, provides valuable insights into a wide range of systems and their behaviors.

Eigenvalues and Eigenvectors: Determining System Behavior

• Definition and significance of eigenvalues in determining the stability and behavior of the system.
• Introduction to eigenvectors and their role in determining the direction of flow.

Eigenvalues and Eigenvectors: Unraveling the Behavior of Differential Equations

In the realm of differential equations, eigenvalues and eigenvectors emerge as crucial gauges for deciphering the stability and dynamics of a system. These elusive mathematical constructs hold the key to unlocking the secrets of how solutions behave over time.

An eigenvalue is a special value that, when plugged into a system’s characteristic equation, results in a non-trivial solution. These numerical gems provide invaluable insights into the stability of a system. Positive eigenvalues signal an unstable system, indicating that solutions will diverge over time. Conversely, negative eigenvalues suggest stability, ensuring that solutions will converge towards a steady-state equilibrium.

Eigenvectors, on the other hand, are vectors that, when multiplied by the system matrix, align perfectly with the direction of the solution. They serve as signposts, guiding us towards the paths that solutions will trace as they evolve through time and space.

Understanding eigenvalues and eigenvectors is paramount in comprehending the dynamics of differential equations. By analyzing these mathematical quantities, we can determine whether a system will exhibit stability, divergence, or any other fascinating behavior. This knowledge is the foundation upon which we build our understanding of a wide range of phenomena, from the fluttering of a butterfly’s wings to the orbits of celestial bodies.

Trace: A Key Factor in System Behavior

In the realm of differential equations, understanding the behavior of a system is crucial. One key concept that plays a significant role in this comprehension is the trace of a matrix, which is the sum of its eigenvalues.

The trace provides valuable insights into the stability of a system. A positive trace indicates an unstable system, while a negative trace signifies a stable system. This is because a positive trace implies the presence of at least one positive eigenvalue, leading to exponential growth of solutions. Conversely, a negative trace ensures the absence of positive eigenvalues, resulting in a decay of solutions.

Trace and Equilibrium Points

The trace is closely tied to the equilibrium points of a system. These points represent states where the system remains constant over time. By analyzing the trace of the matrix associated with the differential equation, we can determine the type of equilibrium point.

If the trace is zero, the equilibrium point is a stable node, indicating that solutions converge to the equilibrium point over time. However, if the trace is positive, the equilibrium point becomes an unstable node, implying that solutions diverge away from it.

A Real-World Application

The concept of trace is not just limited to abstract mathematical equations; it finds practical applications in various fields. For instance, in ecology, the trace can help us analyze the dynamics of population growth. By examining the trace of a matrix representing population interactions, ecologists can determine the stability of the ecosystem.

In conclusion, the trace of a matrix is a fundamental concept in differential equations that provides crucial information about the stability of a system and the behavior of its equilibrium points. Whether you’re investigating population dynamics or analyzing the flow of a fluid, understanding the trace can unlock valuable insights into the underlying system.

Determinant: Product of Eigenvalues

• Definition of determinant as the product of eigenvalues and its relationship to system behavior.

Determinant: Unraveling System Behavior

In the realm of differential equations, the determinant emerges as a critical determinant, offering insights into the underlying dynamics of a system. Determinant is defined as the product of eigenvalues, providing a concise representation of the system’s behavior.

The determinant plays a pivotal role in determining the stability of a system. When the determinant is positive, the system is stable, indicating that solutions will converge towards equilibrium points. Conversely, a negative determinant signals an unstable system, characterized by solutions that diverge from equilibrium points.

Moreover, the determinant provides essential information about the type of equilibrium point a system possesses. A negative trace (sum of eigenvalues) coupled with a positive determinant indicates a stable node, where solutions asymptotically approach the equilibrium point. Conversely, a positive trace and a negative determinant reveal an unstable saddle point, where solutions exhibit diverging trajectories.

Understanding the determinant empowers us to predict the behavior of a system. For instance, a positive determinant and positive eigenvalues suggest that the system exhibits exponential growth or decay. In contrast, a negative determinant and negative eigenvalues indicate oscillatory behavior, where solutions fluctuate around the equilibrium point.

The determinant serves as an invaluable tool in the analysis of differential equations. It provides a compact yet powerful representation of system behavior, enabling us to make informed predictions about the stability and dynamics of a given system.

Phase Portrait: Unveiling the Dynamics of Differential Equations

In the realm of differential equations, phase portraits emerge as powerful visual tools that illuminate the intricate dance of solutions. By plotting the flow of the system in a two-dimensional space, phase portraits provide a comprehensive snapshot of the system’s behavior.

To construct a phase portrait, we map each point in the phase space (a two-dimensional space where the variables of the differential equation are plotted) to a vector representing the direction of motion at that point. These vectors, known as the slope field, create a tapestry of arrows that depicts the system’s flow.

Interpreting Phase Portraits

Phase portraits offer a wealth of insights into the system’s dynamics. Critical points, where the slope field vanishes, play a crucial role. These points are the resting points of the system, revealing where solutions tend to accumulate or diverge.

Stability of Critical Points

The behavior of solutions around critical points is dictated by the eigenvalues of the system’s Jacobian matrix. Stable equilibrium points attract nearby solutions, indicating a stable system. Conversely, unstable equilibrium points repel nearby solutions, suggesting an unstable system.

Flow Lines and Integral Curves

Phase portraits also reveal the trajectories of solutions. Flow lines represent the actual paths taken by solutions as they evolve over time. Integral curves are the curves that correspond to specific solutions of the differential equation.

Phase portraits empower us to visualize the evolution of systems in a dynamic and intuitive way. They are invaluable tools for understanding the behavior of differential equations, offering insights into the stability of solutions and the overall dynamics of the system.

Flow Lines: Mapping the Paths of Solutions

In the realm of differential equations, slope fields provide a vivid representation of the behavior of solutions. Imagine a slope field as a tapestry woven with vectors, each pointing in the direction of the solution at that particular point. These vectors guide us in tracing the flow lines, which are curves that depict the trajectories of solutions.

Drawing flow lines from the slope field is akin to navigating a river’s currents. Starting from a given point, we follow the direction indicated by the vector at that point. Step by step, we trace the path of the solution, observing how it meanders through the slope field.

By studying the flow lines, we gain insights into the behavior of the system. Do the solutions converge towards a stable equilibrium point? Do they spiral outwards, indicating instability? Or do they oscillate periodically? The flow lines provide a visual narrative of the solution’s journey.

In essence, flow lines are invaluable tools for understanding the dynamics of differential equations. They allow us to visualize the trajectories of solutions, predict their behavior, and gain a deeper appreciation for the interplay between differential equations and the real world.

Integral Curves: Solution Curves

• Definition of integral curves as solution curves to the differential equation.
• Identifying integral curves from the slope field and analyzing their relationship to flow lines.

Integral Curves: Unveiling the Paths of Solutions

In the realm of differential equations, where the movement of systems is described through mathematical expressions, the concept of integral curves plays a pivotal role. Integral curves, also known as solution curves, are the graphical representations of solutions to these equations.

Identifying Integral Curves: The Key to Understanding

The intricate network of lines in a slope field, where each line represents the direction of change at a given point, holds the secrets to identifying integral curves. By tracing these lines, we can visualize the trajectory of solutions as they evolve over time.

A Guiding Force: Flow Lines

Integral curves are intimately connected to another essential concept: flow lines. Flow lines depict the actual paths followed by solutions as they move through the slope field. By carefully following the flow lines, we can gain insights into the behavior of the system and the nature of its solutions.

Integral Curves vs. Flow Lines: A Subtle Distinction

While integral curves and flow lines share similarities, it is crucial to note their subtle distinction. Flow lines provide a qualitative representation of the system’s dynamics, while integral curves offer a more precise mathematical description. Integral curves are defined as solutions to the differential equation, passing through specific initial conditions.

Understanding integral curves is indispensable for unraveling the mysteries of differential equations. They empower us to visualize the behavior of systems, anticipate their trajectories, and make informed predictions. Their applications extend far beyond the classroom, encompassing fields such as physics, engineering, and ecology, where they aid in modeling and analyzing complex phenomena.