Simplify And Add Radicals: A Step-By-Step Guide For Beginners

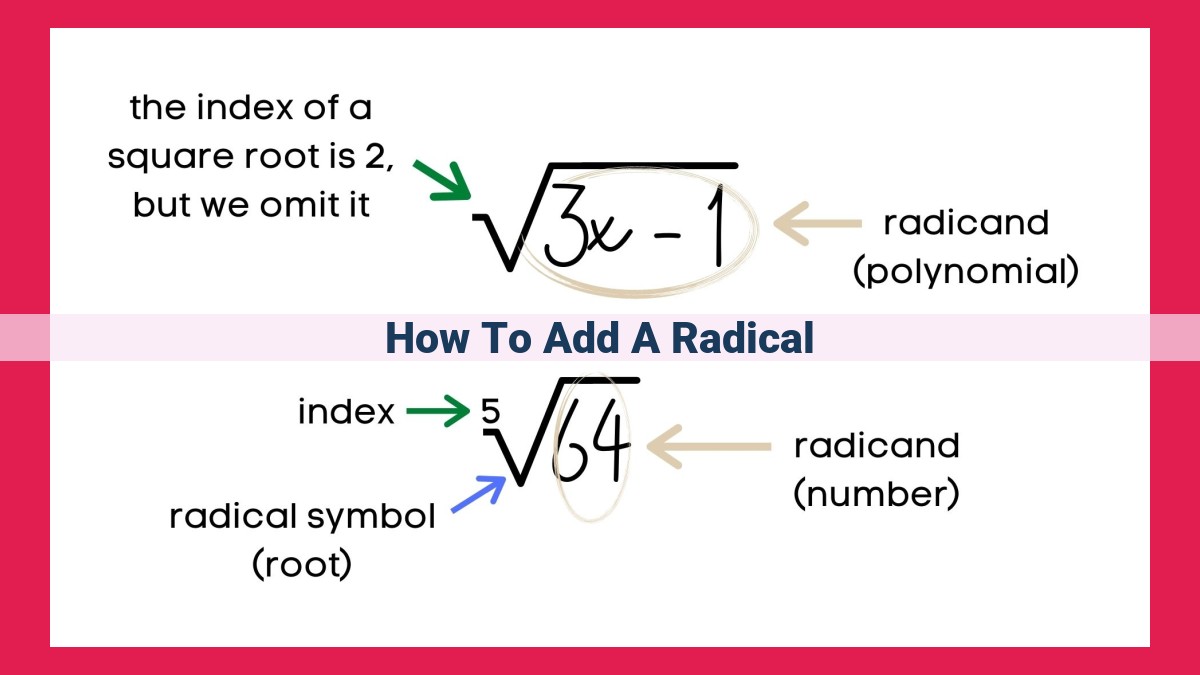
To add radicals, first simplify them to have the same index and radicand. If the radicands are different, they cannot be added directly. For like radicals (with the same index and radicand), add their coefficients and keep the radical unchanged. For unlike radicals, rationalize the denominator of one radical using its conjugate. Multiply both numerator and denominator by the conjugate to create an equivalent expression with a rational denominator. Now, you can add or subtract the radicals.

Understanding Radicals: A Basic Overview

In the realm of mathematics, radicals hold a place of prominence, unlocking the doors to a world of complex expressions. A radical is a mathematical symbol that represents the square root of a number. For instance, the square root of 9 is represented as √9, which simplifies to 3.

Radicals play a pivotal role in various mathematical operations, including addition, subtraction, multiplication, and division. Understanding how to manipulate radicals is essential for solving equations and simplifying expressions.

Adding and Subtracting Radicals

When adding or subtracting radicals, it’s crucial to determine if they are like radicals or unlike radicals. Like radicals have the same radicand, which is the number or variable within the square root symbol. For instance, √5 and √5 are like radicals, whereas √3 and √7 are unlike radicals.

To add like radicals, simply add their coefficients and keep the same radicand. For example:

√5 + √5 = 2√5

Adding unlike radicals is not possible without further simplification. We must first rationalize the denominators to make them like radicals.

Rationalization

Rationalizing the denominator involves multiplying both the numerator and denominator of a fraction by a suitable factor to eliminate irrational denominators. This is commonly used when adding or subtracting fractions involving radicals.

For instance, to rationalize the denominator of (1/√2), we multiply both the numerator and denominator by √2:

(1/√2) * (√2/√2) = √2 / 2

Multiplication and Division of Radicals

Multiplying radicals is straightforward. Simply multiply the coefficients and multiply the radicands under a single radical symbol. For example:

√3 * √7 = √(3 x 7) = √21

Dividing radicals involves rationalizing the denominator if necessary. Once both radicals have rational denominators, divide the coefficients and divide the radicands under a single radical symbol.

Radicals are indispensable tools in the mathematician’s toolkit. Understanding their properties and operations empowers us to simplify complex expressions, solve equations, and navigate the intricate world of mathematical calculations. Whether you’re a seasoned mathematician or just starting to explore the realm of numbers, mastering radicals will unlock new possibilities in your mathematical journey.

Similar Radicals: Unlocking the Secrets of Radical Operations

In the realm of mathematics, radicals play a pivotal role in solving complex equations and expressing real-world phenomena. Similar radicals, in particular, are a subset of radicals that share certain properties, making them remarkably easy to work with. Understanding these properties can supercharge your problem-solving abilities.

Definition of Similar Radicals

Similar radicals are radicals that have the same radicand, which is the expression inside the radical symbol. For example, √(x) and √(y) are similar radicals because both have the radicand x. They share the same index (in this case, 2), which is the small number outside the radical symbol.

Operations on Similar Radicals

Similar radicals can be combined, multiplied, and divided using a set of simple rules. These operations help us simplify and solve complex expressions involving radicals.

• Combining: To combine similar radicals, simply add the coefficients in front of the radical signs and leave the radicand the same. For example, 2√(x) + 3√(x) = 5√(x).

• Multiplying: To multiply similar radicals, multiply the coefficients and the radicands separately. For example, (2√(x)) * (3√(y)) = 6√(xy).

• Dividing: To divide similar radicals, divide the coefficients and the radicands separately. For example, (6√(x)) / (2√(y)) = 3√(x/y).

Examples

Let’s solidify our understanding with some examples:

• Simplify √(4x) + √(9x).

Solution: Both terms have the same radicand (x), so we can combine them to get: √(4x + 9x) = √(13x).

• Multiply (2√(5)) * (3√(10)).

Solution: Multiplying the coefficients and the radicands, we get: (2 * 3)√(5 * 10) = 6√(50) = 6√(25 * 2) = 6(5√(2)).

• Divide (12√(x)) / (4√(y)).

Solution: Dividing the coefficients and the radicands, we get: (12 / 4)√(x/y) = 3√(x/y).

Mastering the operations on similar radicals will empower you to tackle a wide range of mathematical problems with confidence. Don’t hesitate to unleash your inner radical solver!

Adding and Subtracting Radicals: A Journey Through Mathematical Roots

In the realm of mathematics, radicals play a pivotal role, unlocking the secrets of roots and irrational numbers. Adding and subtracting radicals is a fundamental operation, empowering us to explore the intricate world of these elusive quantities.

Before embarking on this mathematical voyage, let’s grasp the difference between like and unlike radicals. Like radicals share the same index (the number outside the radical symbol) and same radicand (the expression inside the radical symbol). Unlike radicals, on the other hand, have different indices or radicands.

To simplify radicals before adding or subtracting them, we aim to make like radicals. This process involves extracting perfect squares from the radicand. For instance, to simplify √12, we first find a perfect square that divides evenly into 12, which is 4. So, √12 = √(4 × 3) = 2√3.

Now, let’s dive into adding and subtracting like radicals. Similar to integers and fractions, like radicals can be combined directly by adding or subtracting their coefficients. For example, 3√5 + 2√5 = 5√5. Note that the radicand remains unchanged during this operation.

In contrast, adding and subtracting unlike radicals requires a bit more finesse. We need to first simplify the radicals to make them like radicals. This can be achieved using techniques like factoring or rationalizing the denominator. Once the radicals are simplified to like radicals, we can combine them as usual.

For instance, let’s add √6 + √10. We first rationalize the denominator of √10 by multiplying it with its conjugate, which is √10. This gives us √6 + (√10 × √10) = √6 + 10.

Combining fractions involving radicals is also fairly straightforward. The key is to find a common denominator, which is a radical expression that can divide evenly into the denominators of both fractions. Once you have the common denominator, you can add or subtract the fractions as usual.

Whether you’re dealing with like or unlike radicals, the ability to add and subtract them is essential for solving a wide range of mathematical problems. By understanding the concepts and techniques outlined in this post, you’ll be well-equipped to navigate the world of radicals with confidence.

Rationalizing the Denominator: A Mathematical Maneuver

Imagine yourself as a fearless adventurer exploring the vast realm of mathematics. On your journey, you encounter a formidable foe – an expression with an irrational denominator. Fear not, for you possess a secret weapon: rationalizing the denominator.

Unveiling the Rationalizing Mission

Rationalizing the denominator is a technique employed to transform an irrational denominator into a rational one. This mathematical sleight of hand makes it possible to perform operations on fractions involving radicals without introducing imaginary numbers.

The Power of Conjugates

Conjugates, those magical pairs of expressions, play a pivotal role in this endeavor. A conjugate is formed by changing the sign between the radical and the radicand. For instance, the conjugate of √(a+b) is √(a-b).

The Rationalization Process

To rationalize a denominator involving a radical, you need to multiply both the numerator and the denominator by the conjugate of the denominator. This seemingly simple step transforms the expression into an equivalent form with a rational denominator.

For example, consider the expression:

1 / √(3+5)

Multiplying both the numerator and the denominator by the conjugate √(3-5):

= 1 / √(3+5) * √(3-5) / √(3-5)

Simplifying the numerator:

= √(3-5) / (√(3+5) * √(3-5))

Using the property that the product of two square roots is the square root of the product:

= √(3-5) / √((3+5) * (3-5))

Finally, simplifying the denominator:

= √(3-5) / √(-8)

And there you have it! The irrational denominator has been vanquished, replaced by a rational one.

By mastering the art of rationalizing denominators, you gain the power to navigate the complex world of radical expressions with ease. So, embrace this technique and equip yourself for your next mathematical adventure.

Conjugates: A Powerful Tool in the Realm of Radicals

In the enigmatic world of mathematics, where the language of numbers and symbols unfolds, the concept of conjugates emerges as a formidable ally in navigating the treacherous terrain of radical expressions. Conjugates, like mathematical magicians, possess the power to transform complex expressions into simpler forms, revealing their hidden elegance.

What are Conjugates?

In the realm of radicals, conjugates are two expressions that are mirror images of each other, differing only in the presence (or absence) of a minus sign. For instance, the conjugate of √2 is -√2, and the conjugate of 3 + √5 is 3 – √5.

Their Role in Rationalizing Denominators

Conjugates play a pivotal role in the process of rationalizing denominators. This technique involves transforming a fraction with an irrational denominator into an equivalent fraction with a rational denominator. By multiplying the numerator and denominator of the fraction by the conjugate of the denominator, we banish the pesky irrationality from the denominator.

Consider the fraction √5/√2. Its conjugate is √2/√2. Multiplying both the numerator and denominator by √2/√2 yields:

(√5/√2) * (√2/√2) = (√5 * √2) / (√2 * √2) = 2√10 / 2 = √10

Ta-da! The denominator is now a rational number, making our fraction more palatable.

Conjugates and Expression Simplification

Conjugates also shine brightly when it comes to simplifying radical expressions. By multiplying two radicals together using their conjugates, we can often streamline the expression into a more manageable form.

For example, let’s tame the expression:

(√2 + √3) * (√2 - √3)

Using the conjugates of √2 ± √3 (which are √2 ∓ √3), we get:

(√2 + √3) * (√2 - √3) = (√2 + √3) * (√2 - √3) * (√2 + √3) / (√2 + √3) = 2 - 3 = -1

Conjugates, those unsung heroes of the mathematical world, are indispensable tools for tackling radical expressions. Their ability to rationalize denominators and simplify expressions makes them a formidable force in the realm of mathematics. Embrace their power, and conquer the challenges of radicals with newfound confidence.

Rational Exponents: A Shortcut to Simplify Radicals

Have you ever wondered if there’s a quicker way to simplify complicated radicals? Enter rational exponents—mathematical heroes that will help you turn those pesky roots into manageable fractions.

In the realm of mathematics, roots represent the inverse of exponents. Just as the square root of 9 is 3 because 3² = 9, the cube root of 27 is 3 because 3³ = 27. Now, let’s introduce rational exponents, which are fractions representing the power to which a number is raised.

For example, instead of writing √x² we can write x^(1/2), indicating that the base x is raised to the power of 1/2. This means that x^(1/2) = √x since √x is the same as raising x to the power of 1/2.

Rational exponents become even more powerful when dealing with radicals in fractions. Let’s take a look at 1/√2. Using rational exponents, we can rewrite this as 2^(-1/2). Now, we can use the rule for multiplying fractions with exponents to simplify:

1/2^(-1/2) = 1 * 2^(1/2) = 2^(1/2) = √2

This shows how rational exponents can simplify expressions by converting them into fractions that can be easily evaluated. Whether you’re a math whiz or just starting to explore the world of radicals, rational exponents are a valuable tool that will help you conquer any radical challenge.

The Radicand: The Heart of the Radical

In the world of mathematics, radicals are expressions that involve roots and can seem intimidating at first glance. However, understanding the concept of the radicand, the heart of the radical, can make working with radicals much more manageable.

The radicand is the quantity inside the radical sign. It can be a number, a variable, or even an algebraic expression. For example, in the radical expression √(x + 2), the radicand is (x + 2).

Identifying the radicand is crucial because it determines the value of the radical. For instance, √(9) equals 3, because when 3 is squared, we get 9, the radicand. In √(-4), the radicand is -4, indicating that the square root of -4 is an imaginary number.

Operations involving radicals often require simplifying the radicand first. For instance, √(12) can be simplified by factoring the radicand into √(4 * 3) = √4 * √3 = 2√3.

Understanding the radicand is vital for performing radical operations accurately. It enables you to determine the value of the radical, simplify expressions, and manipulate radicals effectively. Remember, the radicand is the core component that governs the behavior of radicals in mathematical calculations.