Shifting Parabolas Right: A Comprehensive Guide For Equation Translations

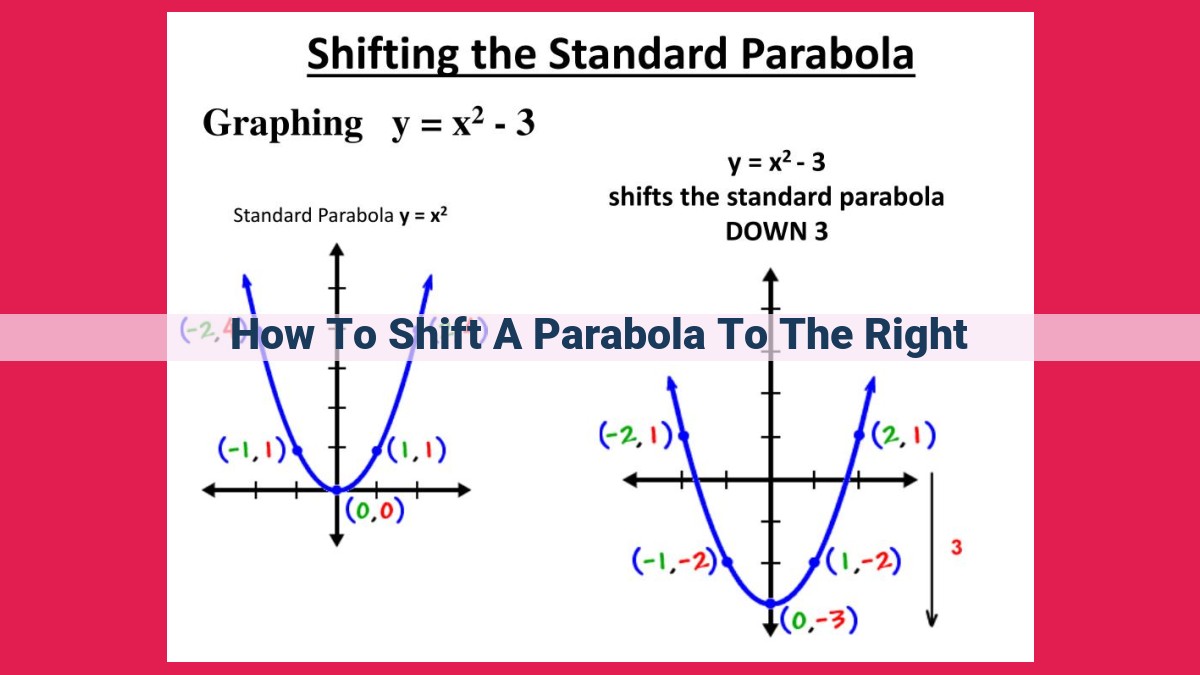
To shift a parabola to the right, apply a translation to the equation in the form y = f(x – h), where h is the number of units to shift to the right. This moves the entire parabola h units to the right on the x-axis, with the vertex and all other points following suit. Each x-coordinate in the original equation increases by h, resulting in a new parabola that is congruent to the original parabola but shifted to the right.

Translation and Shifting Parabolas to the Right: Unveiling the Patterns

In the realm of mathematics, parabolas dance across the coordinate plane, gracing equations with their graceful curves. Understanding how to shift these parabolas is crucial for unlocking their secrets. Let’s journey into the world of translating parabolas to the right and unravel the fascinating patterns that guide their movement.

What’s Translation All About?

In mathematical terms, translation refers to the movement of an object from one point to another without altering its shape or size. As it pertains to parabolas, this means moving the entire parabola horizontally without changing its fundamental shape.

Shifting Right: A Story of Equation Tweaks

Imagine a parabola with an equation of y = (x – 2)^2 + 3. Its vertex is at the point (2, 3), and it opens upward. Now, let’s shift it to the right by 4 units. This means that every point on the original parabola will move 4 units to the right.

The new equation of the shifted parabola is y = (x – 6)^2 + 3. Notice the pattern? When you shift a parabola to the right by h units, you subtract h from the x-coordinate within the parentheses of the equation.

Examples That Illuminate the Path

Let’s solidify our understanding with a few examples:

• Original Equation: y = (x + 1)**^2 – 5

• Shift Right by 3 Units: y = (x – 2)**^2 – 5

• Original Equation: y = -2(x – 4)**^2 + 1

• Shift Right by 5 Units: y = -2(x – 9)**^2 + 1

By understanding the translation principle, we can effortlessly shift parabolas to the right and unravel the mysteries they hold.

Adding Constants to Shift Parabolas Vertically

• Explain how adding a constant to a parabola’s equation affects its vertical position.
• Show how the sign of the constant determines whether the parabola shifts up or down.
• Give examples of how to shift a parabola vertically using the “addition” method.

Shifting Parabolas Vertically with Constants

When it comes to parabolas, understanding how to shift them vertically is crucial for graphing and solving equations. One way to do this is by adding constants to their equations.

Let’s delve into how this works. When you add a constant to a parabola’s equation, it shifts the parabola vertically. The magnitude of the constant determines the distance of the shift, while its sign determines the direction.

For instance, if you add a positive constant, the parabola shifts upward. This is because adding a positive value to the equation makes the output (y-coordinate) larger for any given input (x-coordinate).

Conversely, adding a negative constant shifts the parabola downward. This is because a negative value reduces the output, causing the parabola to move closer to the x-axis.

To illustrate this further, let’s take a basic parabola equation, f(x) = x^2. If we add a constant of 2 to this equation, we get f(x) = x^2 + 2. By adding 2 to the equation, we have effectively shifted the parabola 2 units upward.

Example: Graph the parabolas f(x) = x^2 and f(x) = x^2 + 2. Notice how the second parabola is shifted 2 units up from the first one.

Shifting parabolas vertically is a valuable technique for solving equations and modeling real-world scenarios. For example, it can be used in:

• Projectile motion: Modeling the path of a projectile by factoring in its initial velocity and gravitational acceleration.
• Resource allocation: Optimizing resource distribution by considering constraints and priorities.
• Financial analysis: Predicting future trends by shifting historical data points based on projected growth rates.

By understanding the concept of adding constants to shift parabolas vertically, you can enhance your problem-solving abilities and gain a deeper understanding of mathematical modeling.

Vertical Shift and Addition

• Relate vertical shift to the concept of addition.
• Explain how adding a positive constant to the y-coordinate of the vertex shifts the parabola upward.
• Demonstrate how subtracting a positive constant shifts the parabola downward.

Understanding Vertical Shift in Parabolas

In the realm of mathematics, parabolas play a captivating role in describing a wide range of real-world phenomena. Imagine a cannonball hurtling through the air or a rocket soaring into space. The trajectory of these objects can be modeled using parabolas, and understanding how to shift them is crucial for predicting outcomes.

One key concept in parabola manipulation is vertical shift. This refers to moving the entire parabola up or down the y-axis without altering its overall shape. The fascinating thing about vertical shift is that it can be directly linked to addition.

Adding Constants and Vertical Placement

When we add a positive constant to the y-coordinate of a parabola’s vertex, the parabola shifts upward. This is because the vertex is the highest or lowest point on the parabola, and adding to its y-coordinate elevates the entire curve. Conversely, subtracting a positive constant from the y-coordinate of the vertex shifts the parabola downward.

For example, let’s consider the parabola defined by the equation y = x^2. Its vertex is located at the origin (0, 0). Adding a constant of 3 to the y-coordinate of the vertex gives us the new equation y = x^2 + 3. This new parabola is shifted 3 units upward from the original parabola.

Visualizing the Shift

The image below illustrates the vertical shift of parabolas. The blue parabola represents the original function, while the red parabola represents the function shifted 3 units upward.

[Image of two parabolas, one blue and one red, shifted vertically relative to each other. The blue parabola is labeled as y = x^2, and the red parabola is labeled as y = x^2 + 3.]

As you can see, the red parabola is vertically translated by 3 units, but its shape remains the same. This shift can be applied to any parabola, regardless of its opening direction or equation.

Applications in Real-World Scenarios

Understanding vertical shift is not only a mathematical concept but also a valuable tool in various real-world applications:

• Projectile motion: By adding a constant to the y-coordinate of a parabolic trajectory, we can account for the initial height of the object being launched.
• Resource allocation: Shifting parabolas vertically can help us optimize the distribution of resources by maximizing the intersection points between different functions.
• Financial data analysis: By considering the vertical shift of financial curves, we can identify key trends and predict future outcomes.

Vertex Change and Equation Change: Delving into the Heart of Shifting Parabolas

As we delve deeper into the world of parabolas, let’s explore how changing the vertex, the heart of the parabola, affects its equation.

The Role of the Vertex

The vertex of a parabola represents its highest or lowest point. When we shift a parabola, the vertex is the reference point that determines the direction and amount of the shift.

Equation Transformation

Changing the coordinates of the vertex has a direct impact on the equation of the parabola. In general, when the vertex is moved horizontally (changing the x-coordinate), the equation is transformed by adding or subtracting a constant from the x-term.

For example, if we shift the parabola right by 3 units, we add 3 to the x-coordinate of the vertex in the equation. Similarly, shifting left by 2 units involves subtracting 2 from the x-term.

On the other hand, when the vertex is moved vertically (changing the y-coordinate), the equation is transformed by adding or subtracting a constant from the y-term.

If the parabola is shifted up by 4 units, we add 4 to the y-coordinate of the vertex in the equation. Conversely, shifting down by 5 units entails subtracting 5 from the y-term.

Finding the New Vertex and Equation

To find the new vertex and equation after a vertex change, follow these steps:

1. Determine the shift direction and amount: Identify whether the vertex is moved horizontally or vertically and by how many units.

2. Modify the coordinates of the vertex: Add or subtract the shift amount to the original x- or y-coordinate of the vertex.

3. Adjust the equation: Based on the shift direction, add or subtract the appropriate constant from the x- or y-term in the original equation.

By understanding the connection between vertex change and equation change, we gain a deeper comprehension of parabola transformations and their applications in various fields.

Equation Change and Vertex Change: Exploring the Interplay

When exploring the world of parabolas, we often encounter the need to move them around the coordinate plane. While the translation method and addition of constants allow us to shift parabolas vertically or horizontally, the equation change method offers an alternative approach to this task.

By manipulating the equation of a parabola, we can indirectly influence the position of its vertex. This method proves particularly useful when we want to shift a parabola in both the horizontal and vertical directions simultaneously.

Let’s consider the general equation of a parabola: y = a(x – h)² + k. The coordinates of its vertex are (h, k). Changing the value of k shifts the parabola vertically. A positive value of k moves the vertex and the entire parabola upward, while a negative value shifts them downward. The value of h, on the other hand, affects the parabola’s horizontal position. Increasing h shifts the vertex and the parabola to the right, whereas decreasing h moves them to the left.

To illustrate this concept, let’s consider two examples. Suppose we have the parabola y = (x – 2)² + 3. Its vertex is at (2, 3). If we add 5 to the equation, we get y = (x – 2)² + 8. This shifts the vertex upward by 5 units, resulting in the new parabola y = (x – 2)² + 8 with its vertex at (2, 8).

Now, let’s change h to 4. This gives us the equation y = (x – 4)² + 3. In this case, the vertex moves two units to the right, resulting in the new parabola y = (x – 4)² + 3 with its vertex at (4, 3).

Understanding the relationship between equation change and vertex change empowers us to manipulate parabolas efficiently. By skillfully altering the equation, we can precisely position the parabola on the coordinate plane, adapting it to various mathematical models and real-world applications.

Applications of Shifting Parabolas

In the realm of mathematics, parabolas play a pivotal role in modeling and analyzing various real-world phenomena. Shifting parabolas is a fundamental technique that allows us to manipulate these curves to fit specific scenarios. Here are a few compelling applications of shifting parabolas:

Modeling Projectile Motion:

Parabolas serve as the perfect tool to describe the trajectory of projectiles. By shifting parabolas vertically, we can adjust the initial velocity and horizontally to account for wind resistance. This enables us to track the path of a thrown object or a missile with precision.

Optimizing Resource Allocation:

In resource management, shifting parabolas enables us to find the optimal allocation plan. By shifting parabolas along the x-axis, we can identify the quantities of different resources that satisfy specific requirements while shifting parabolas along the y-axis determines the associated costs.

Analyzing Financial Data:

Parabolas are widely used in financial analysis. By shifting parabolas vertically, we can model the growth of investments or the decline of stock prices. This allows investors and analysts to make informed decisions based on predicted market trends.

Shifting parabolas is a powerful technique that extends the versatility of these curves beyond theoretical concepts. From simulating projectile motion to optimizing resource allocation and analyzing financial data, shifting parabolas empowers us to tackle real-world problems with remarkable accuracy and efficiency.