Scalene Triangles: Unique Characteristics And Applications In Design And Engineering

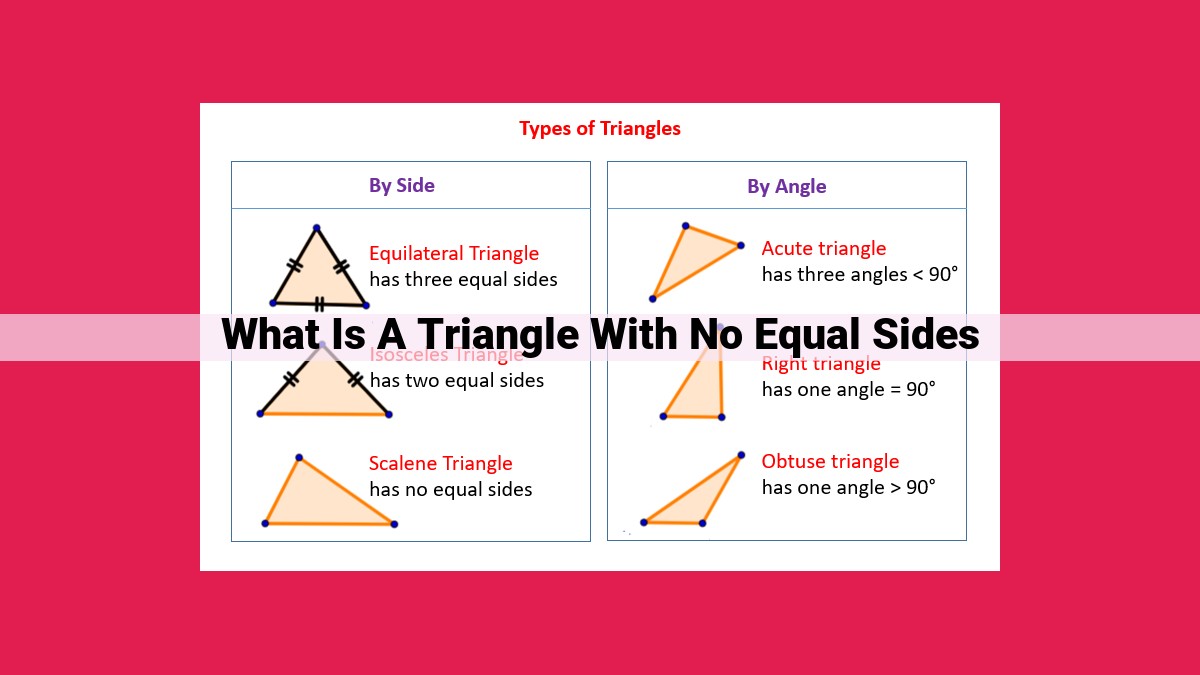
A scalene triangle is a three-sided shape where all sides are unequal. This means that there is no symmetry or balance between its sides, making it a unique type of triangle. Unlike isosceles or equilateral triangles, scalene triangles have different side lengths, resulting in varying angle measures. They are often found in real-world applications, such as roof trusses and bridges, where their unique characteristics contribute to structural stability and design.

The Not-So-Equal Triangle: Delving into the World of Scalene Triangles

In the realm of geometry, there exists a fascinating shape that stands out from the rest: the scalene triangle. It’s a triangle like no other, devoid of any equal sides, making it the epitome of asymmetry.

Imagine a triangle as a closed shape with three sides. In a regular triangle, all three sides have the same length, creating perfect symmetry. But in the case of a scalene triangle, this balance is shattered. No two sides are equal, and this absence of symmetry defines its unique essence.

This lack of equal sides in a scalene triangle has a profound impact on its other properties. Because its sides are unequal, the angles opposite those sides will also vary in size. This asymmetry sets scalene triangles apart from their more symmetrical counterparts.

Examples and Applications of Scalene Triangles

Scalene triangles are not confined to the pages of textbooks but are found in various forms in the real world. Take, for instance, the kites that soar high in the sky. Their frames are often shaped like scalene triangles, providing stability and allowing them to dance gracefully in the wind.

Bridges, too, often incorporate scalene triangles into their design. The trusses that support these structures are often composed of scalene triangles, which provide strength and stability while allowing for efficient load distribution.

Scalene triangles are a testament to the beauty of asymmetry in geometry. Their unique characteristics, defined by their lack of equal sides, make them both fascinating to study and essential for real-world applications. Understanding their properties is crucial for anyone interested in delving deeper into the world of geometry and its practical applications.

Delving into the Term “Scalene”:

• Define the meaning of “scalene” in geometry.
• Emphasize the absence of equal sides as the defining characteristic.

Delving into the Term “Scalene”: The Essence of Inequality

In the realm of geometry, triangles reign supreme as one of the most fundamental shapes. Among these triangles, there exists a unique breed known as scalene triangles, distinguished by their intrinsic inequality. Scalene, a term derived from the Greek word “skalēnos,” meaning “unequal,” perfectly captures the defining characteristic of these triangles: the absence of equal sides.

Unlike their equilateral and isosceles counterparts, scalene triangles possess three sides of unequal lengths. This absence of symmetry and balance between sides sets them apart, making them a fascinating subject of geometric study. The absence of equal sides not only affects the triangle’s proportions but also influences its angle measures, leading to a unique and ever-changing geometric dance.

Understanding the concept of a scalene triangle is crucial for unlocking the intricacies of geometry. By examining their unique properties and exploring their real-world applications, we gain a deeper appreciation for the complex and captivating world of shapes.

Discovering the Scalene Triangle: A Shape of Unequal Sides

Triangles are ubiquitous shapes in our world, from the roofs of our houses to the sails of ships. Among the diverse triangle family, the scalene triangle stands out as a unique entity. Unlike its equilateral and isosceles cousins, the scalene triangle boasts three sides of different lengths, making it a captivating study in asymmetry and variety.

In the realm of geometry, a scalene triangle is defined as a closed three-sided shape where no two sides are of equal length. This fundamental characteristic distinguishes it from other triangle types. The absence of symmetry or balance between sides gives the scalene triangle its distinctive character.

Delving into the Nature of Triangles

Triangles, by their very nature,** are closed three-sided shapes** formed by the intersection of three straight lines. Their sides connect to form three vertices, creating a triangular shape. The unique aspect of a scalene triangle lies in the variation of its side lengths. This variation results in a triangle with no two sides congruent, making it a fascinating specimen in the geometric landscape.

Side Lengths and Their Impact: The Key to Distinguishing Scalene Triangles

In the realm of triangles, where balance and symmetry are often celebrated, the scalene triangle stands as an exception, proudly displaying its unique charm. Unequal sides are its defining characteristic, setting it apart from its more structured counterparts.

The absence of equal sides in a scalene triangle has a significant impact on its angle measures. Unlike isosceles triangles with two equal sides and equal angles, or equilateral triangles with all sides and angles equal, scalene triangles possess distinct angles. Each side length contributes to a different angle, creating a triangle that is truly one of a kind.

This variation in angle measures is directly related to the side length ratios. In a scalene triangle, each pair of sides has a different ratio, leading to different angle measures. For example, a scalene triangle with side lengths 3, 4, and 5 will have three different angles, and none of them will measure 60 degrees, as is the case in equilateral triangles.

It is this absence of symmetry that makes scalene triangles so intriguing. Their unequal sides and varying angles create a dynamic and asymmetrical shape, challenging our preconceptions of geometrical order. Yet, within their asymmetry lies a unique beauty, a testament to the diversity found within the mathematical realm.

Examples and Applications of Scalene Triangles in the Real World

Geometric Examples

• Kites: The iconic shape of a kite, with its two unequal sides and two diagonals, forms a scalene triangle.
• Hexagons: In a regular hexagon, even though all six sides are equal, the triangles connecting adjacent vertices are scalene, with sides of alternating lengths.

Real-World Applications

• Roof Trusses: Structural frameworks used in roof construction often incorporate scalene triangles to provide stability and support.
• Bridges: Suspension bridges, particularly those with asymmetric spans, utilize scalene triangles in their cable arrangements to distribute weight and tension evenly.
• Art and Architecture: Scalene triangles create visual interest and asymmetry in architectural designs and artwork. For instance, the modernist Guggenheim Museum in Bilbao features a roof composed of interconnected scalene triangles.
• Navigation: Sailors use sextants to measure angles between celestial bodies. The triangles formed by the sextant, a ship’s horizon, and various celestial reference points are often scalene, helping determine the vessel’s latitude and longitude.
• Engineering: Scalene triangles are found in various mechanical components, such as gears and brackets, where their unique shape allows for optimal load distribution and strength.