Resonant Frequency: Key Concepts, Equation, And Applications

Resonant frequency, where a system vibrates most, is crucial in fields like engineering and music. It’s related to natural frequency, the inherent vibration rate of a system, and stiffness and mass. The equation for resonant frequency is f = √(k/m), where k is stiffness and m is mass. Understanding resonant frequency helps prevent resonance, excessive vibration that can damage structures, and harness it in applications like tuning instruments or designing shock absorbers.

• Define resonant frequency and its significance in various fields.
• State the purpose of the article: to provide a comprehensive guide on understanding and calculating resonant frequency.

Understanding Resonant Frequency: A Comprehensive Guide

Resonant frequency, a fascinating phenomenon that occurs when a system vibrates at a particular frequency, has profound significance across diverse fields. Imagine a pendulum swinging at its natural pace. That pace is its resonant frequency. Understanding this concept is crucial for engineers, physicists, and musicians alike. In this guide, we delve into the world of resonant frequency, exploring its intricacies and unveiling how to calculate it.

Resonant Frequency: The Sweet Spot of Vibration

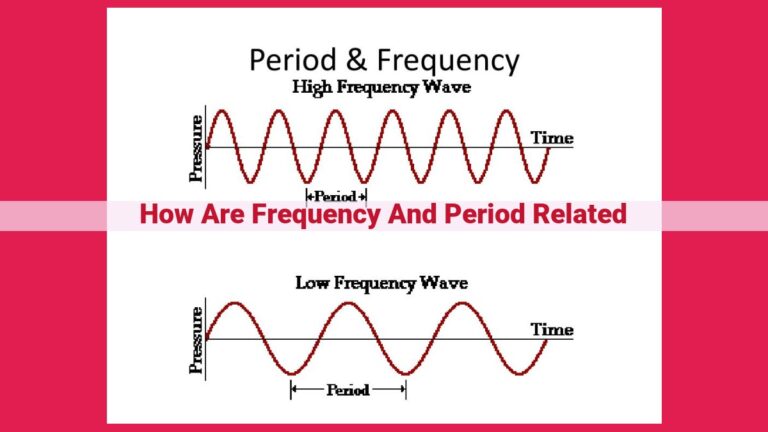
Resonant frequency, the frequency at which a system vibrates most efficiently, is a vital concept in engineering. In a nutshell, it’s the frequency that makes a system resonate, like a guitar string vibrating after you strum it. This phenomenon occurs when the external force applied to the system matches its natural frequency.

Meet Natural Frequency: The System’s Own Rhythm

Every system has a natural frequency, a frequency at which it vibrates without any external force. This intrinsic property depends on two key factors: stiffness and mass. Stiffness refers to how much a system resists deformation, while mass represents the amount of matter it contains. A stiffer system with less mass will have a higher natural frequency, akin to a taut guitar string. Conversely, a less stiff system with more mass will have a lower natural frequency, resembling a slack string on a bass guitar.

Resonant Frequency: The Magic of Alignment

Resonant frequency, the frequency at which a system vibrates with maximum amplitude, happens when external force and natural frequency align. At this point, the system’s response to external force is amplified, resulting in intense vibrations. This is why a gentle push can send a swing soaring high if applied at its resonant frequency.

Natural Frequency

• Define natural frequency as the frequency at which a system vibrates naturally without external force.
• Explain the relationship between natural frequency, stiffness, and mass.
• Provide the equation for calculating natural frequency (f = √(k/m)).

Natural Frequency: The Intrinsic Rhythm of Vibratory Systems

Imagine a child’s swing hanging from a tree branch. When you gently push it, it swings back and forth with an inherent rhythm that seems to beckon you to keep pushing. This rhythm is known as natural frequency, the frequency at which an object vibrates freely without any external force.

Natural frequency is a fundamental property of any vibrating system, be it a swing, a guitar string, or a machine component. It is determined by two key characteristics: stiffness and mass. Stiffness measures how resistant an object is to bending or deformation, while mass measures its resistance to acceleration.

The relationship between natural frequency, stiffness, and mass can be expressed mathematically with the equation:

f = √(k/m)

where:

• f is the natural frequency
• k is the stiffness
• m is the mass

This equation reveals that a stiffer object will have a higher natural frequency, while a heavier object will have a lower natural frequency. In other words, the stiffer and lighter an object is, the faster it will vibrate naturally.

Understanding natural frequency is crucial in various fields, from engineering to music. Engineers use it to design structures that can withstand vibrations, while musicians use it to tune their instruments and create harmonious sounds. By manipulating stiffness and mass, we can harness the power of natural frequency to achieve desired results in a wide range of applications.

Resonant Frequency

• Define resonant frequency as the frequency at which a system exhibits maximum vibration due to external force.
• Explain the relationship between resonant frequency, natural frequency, stiffness, and mass.
• Provide the equation for calculating resonant frequency (f = √(k/m)).

Resonant Frequency: The Symphony of Vibration

In the realm of physics and engineering, the concept of resonant frequency holds immense significance. It’s the frequency at which a system vibrates with maximum amplitude when subjected to an external force. This phenomenon is akin to a perfectly tuned guitar string resonating with the strumming of a pick, or a delicate crystal glass shattering when subjected to a high-pitched sound.

Resonant frequency is intricately connected to a system’s natural frequency, the frequency at which it oscillates freely without any external influence. The relationship between these two frequencies, along with stiffness and mass, is described by the equation f = √(k/m). Here, stiffness (k) represents the resistance of a system to deformation, while mass (m) denotes the amount of matter within the system.

Imagine a simple spring-mass system. When you pull the mass and release it, the system oscillates at its natural frequency, determined solely by the stiffness of the spring and the mass attached to it. However, if you apply an external force at a frequency matching the system’s natural frequency, the amplitude of the oscillations amplifies significantly. This is the point of resonance.

Understanding resonant frequency is crucial in numerous applications. In structural engineering, engineers must ensure that buildings don’t resonate with external vibrations, such as those caused by earthquakes or strong winds. In electrical engineering, resonant frequency determines the optimal operating frequencies for circuits and antennas.

Resonant frequency also plays a vital role in music and sound engineering. Musical instruments, such as violins and drums, are designed to produce specific resonant frequencies that create their unique sounds. By adjusting the tension of strings or the size and shape of instruments, musicians can _fine-tune these resonant frequencies to achieve the desired musical tones.

In conclusion, resonant frequency is a fundamental concept in physics and engineering. It governs the behavior of vibrating systems, from the delicate oscillations of a guitar string to the robust vibrations of bridges. Understanding this phenomenon is essential for designing and optimizing systems in a wide range of applications. Whether it’s preventing structural failures or creating harmonious musical instruments, resonant frequency continues to shape our world in countless ways.

Stiffness: The Gatekeeper of Resonant Frequency

In the realm of resonant frequency, stiffness plays a crucial role as the gatekeeper, regulating the system’s resistance to deformation. Like a stalwart guardian, stiffness determines how much a system will bend or yield when an external force is applied.

The relationship between stiffness, natural frequency, and resonant frequency is an intricate dance. Natural frequency, the system’s inherent tendency to vibrate at a specific frequency, is inversely proportional to stiffness. The stiffer the system, the higher its natural frequency. On the other hand, resonant frequency, the frequency at which the system reaches its peak vibration, is directly proportional to stiffness. The stiffer the system, the higher its resonant frequency.

Understanding this delicate balance is crucial in various fields. For instance, in engineering, designers must carefully balance stiffness to prevent excessive vibrations that could lead to structural failure. In music, instrument makers adjust stiffness to fine-tune the pitch and tone of their creations.

Calculating stiffness is relatively straightforward using the equation k = F/x, where k is stiffness, F is the applied force, and x is the resulting deformation. By understanding the principles of stiffness, you can harness its power to control the resonant behavior of systems, ensuring optimal performance and avoiding potential risks.

Mass: The Heavyweight Influencer

In the realm of vibrating systems, mass plays a pivotal role, acting as a counterweight to the energetic forces of stiffness and frequency. Mass is the physical embodiment of matter within a system, the substance that resists acceleration and dampens vibrations.

Its impact on resonance is inversely proportional: the greater the mass, the lower the system’s tendency to vibrate. This is because a heavier system requires more force to set it in motion, effectively reducing its susceptibility to external vibrations. Conversely, lighter systems, with less mass, respond more readily to external stimuli, making them more prone to resonance at lower frequencies.

The relationship between mass, natural frequency, and resonant frequency can be mathematically expressed as:

f = √(k/m)

where:

• f is the natural frequency or resonant frequency
• k is the stiffness
• m is the mass

As you can see, the mass term (m) appears in the denominator of the equation. This indicates that as mass increases, the natural frequency and resonant frequency decrease. This inverse relationship is crucial for understanding how mass influences the behavior of vibrating systems.

In practical applications, understanding the role of mass is essential. For example, in the design of bridges or buildings, engineers carefully consider the mass of the structure to ensure that it does not resonate with the vibrational frequencies of wind or earthquakes. Conversely, in musical instruments, the mass of the strings or membranes determines the pitch and timbre of the sound produced.

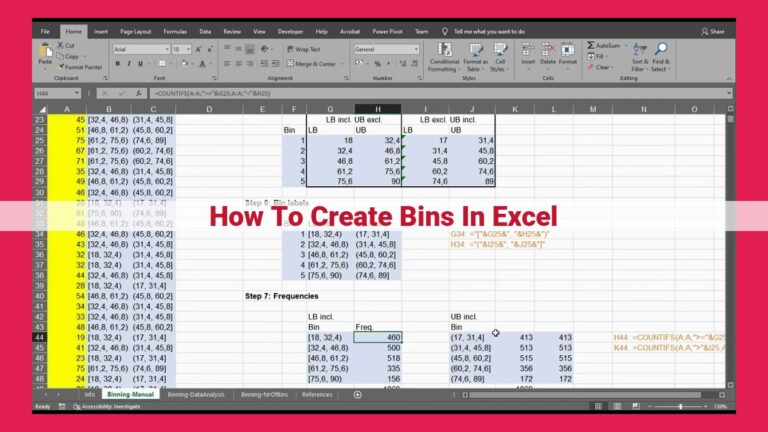
Calculating Resonant Frequency: A Comprehensive Guide

In the world of physics and engineering, understanding resonant frequencies is crucial for designing and optimizing various systems. From musical instruments to mechanical structures, resonant frequencies play a pivotal role. This blog post will provide a comprehensive guide to understanding and calculating resonant frequencies, empowering you to master this fundamental concept.

What is Resonant Frequency?

Every object has a natural frequency at which it vibrates naturally when disturbed. When an external force is applied at this specific frequency, the object exhibits resonance, a state of maximum vibration. This frequency is known as the resonant frequency of the object. Understanding resonant frequencies is essential to avoid potentially damaging vibrations and optimize system performance.

Equation for Resonant Frequency

The resonant frequency (f) of a system is directly related to two key physical properties: stiffness (k) and mass (m). The relationship is expressed by the equation:

f = √(k/m)

Stiffness represents the resistance of an object to deformation, while mass is the measure of its matter content. The equation reveals that a system with a higher stiffness and lower mass will have a higher resonant frequency.

Applying the Equation

To calculate the resonant frequency of a system, you need to determine its stiffness and mass. Here are a few examples to illustrate the application of the equation in different scenarios:

• Pendulum: A pendulum’s stiffness is determined by its length and the acceleration due to gravity (g). The mass is the weight of the pendulum bob. By measuring these parameters and applying the equation, you can calculate the resonant frequency of the pendulum.
• Spring-Mass System: In a spring-mass system, the stiffness is determined by the spring constant, while the mass is the mass of the object attached to the spring. By knowing these values, you can calculate the system’s resonant frequency using the equation.
• Musical Instruments: The resonant frequencies of musical instruments are crucial for their sound quality. Different instruments have different resonant frequencies, which can be adjusted by altering the stiffness or mass of the instrument’s components.

By understanding and applying the equation for resonant frequency, you gain a powerful tool for optimizing and analyzing systems in various fields, from acoustics to engineering.