Discover The Symmetry Of Rectangles: Its Importance And Applications

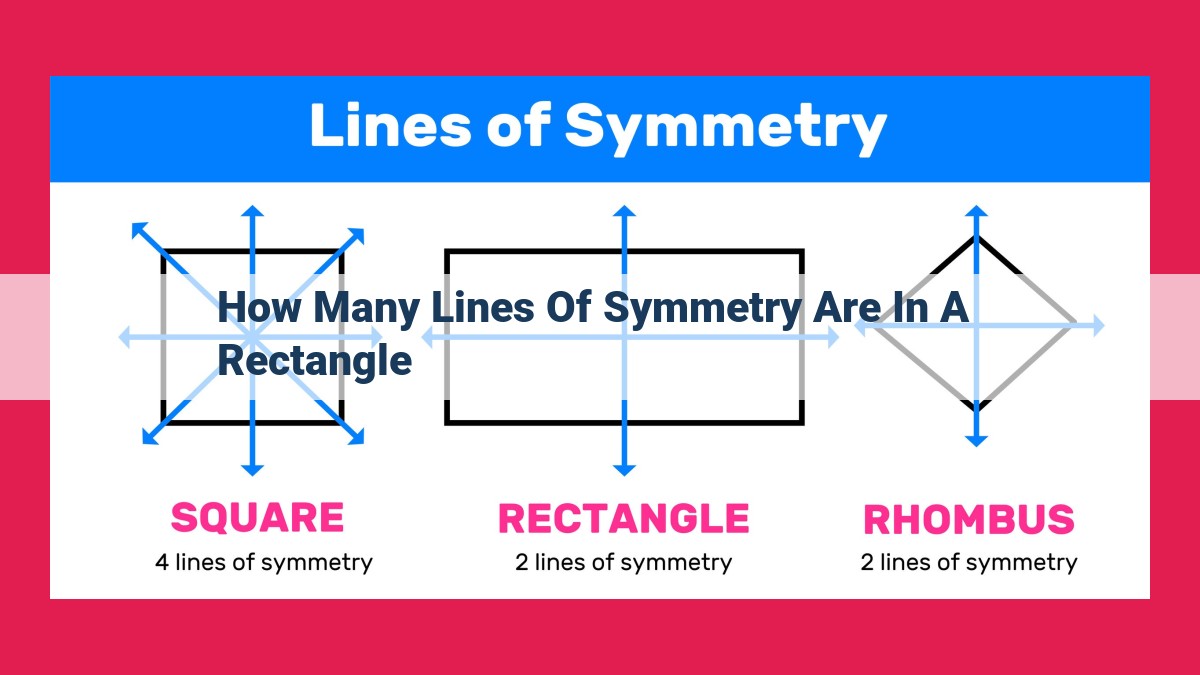
In geometry, a rectangle possesses two distinct lines of symmetry. These lines, perpendicular to each other, bisect opposite sides and intersect at the rectangle’s center. The lines divide the rectangle into four congruent right triangles, exhibiting its symmetrical properties. Understanding these lines of symmetry is crucial in geometric analysis and has practical applications in diverse fields, including architecture, design, and engineering.

The Significance of Rectangles and Lines of Symmetry

Welcome to the fascinating world of geometry, where we explore the remarkable properties of shapes. Today, we zoom in on rectangles, a cornerstone of architecture, engineering, and everyday life. These ubiquitous shapes hold a treasure trove of secrets, and one of their most intriguing features lies in their lines of symmetry.

Defining Rectangles and Lines of Symmetry

A rectangle is a parallelogram with four right angles. It’s like a flattened square, with equal opposite sides and parallel sides. Lines of symmetry are imaginary lines that divide a figure into two congruent (identical) halves. These lines are crucial in geometry, helping us understand the properties of shapes and solve geometric puzzles.

The Importance of Lines of Symmetry

Lines of symmetry aren’t just abstract concepts; they have profound implications in the real world. Architects use them to create balanced and aesthetically pleasing buildings, while engineers leverage them to design strong and stable structures. Even in nature, lines of symmetry can be found in the intricate patterns of snowflakes and the delicate veins of leaves.

Concept: Unveiling the Two Lines of Symmetry in Rectangles

In the realm of geometry, rectangles stand out as captivating figures characterized by their precise angles and well-defined sides. Amidst these defining features lies a hidden elegance: the presence of exactly two lines of symmetry.

Defining Lines of Symmetry: A Gateway to Understanding

Imagine a line that divides a figure into mirror images, where one side perfectly reflects the other. This is the essence of a line of symmetry. Its significance extends beyond mere aesthetics, serving as a fundamental tool for analyzing geometric shapes and uncovering their hidden relationships.

Rectangles and Symmetry: A Perfect Pair

Delving deeper into rectangles, we discover that they possess a unique property: they are adorned with precisely two lines of symmetry. These lines intersect at the rectangle’s heart, dividing it into four congruent quadrants. Their existence stems from the rectangle’s inherent symmetry, where opposite sides and angles mirror each other with flawless precision.

Feature: Bisection of Opposite Sides and Intersection at the Center

In the realm of geometry, lines of symmetry play a pivotal role, and rectangles stand out as prime examples of figures that possess two distinct lines of symmetry. These lines not only divide the rectangle into congruent parts, but they also exhibit unique properties that are essential for understanding the geometric intricacies of rectangles.

A line that bisects a segment is a line that passes through the segment’s midpoint, effectively dividing it into two equal parts. In the case of a rectangle, both lines of symmetry bisect opposite sides. This means that each line divides one side of the rectangle into two segments of equal length, and it divides the opposite side into two segments of equal length.

For instance, consider a rectangle with a length of 10 units and a width of 6 units. If we draw a line of symmetry along the length, it will divide the length into two segments of 5 units each. Similarly, if we draw a line of symmetry along the width, it will divide the width into two segments of 3 units each.

Furthermore, the lines of symmetry in a rectangle possess another notable property: they intersect at the center of the rectangle. This point, often referred to as the centroid, is where all three pairs of parallel sides intersect. In our previous example, the center would be the point where the two lines of symmetry intersect, dividing the rectangle into four equal right triangles.

These properties of the lines of symmetry are not only intriguing from a geometric perspective but also have practical applications. For instance, the ability to bisect opposite sides is crucial for determining the midpoint of a rectangle, which is important for various architectural and design tasks. Additionally, understanding the intersection of the lines of symmetry at the center is essential for calculating the center of mass of a rectangle, which is a key consideration in engineering and physics.

In conclusion, the lines of symmetry in a rectangle are not just arbitrary lines; they possess specific properties, such as the bisection of opposite sides and the intersection at the center, that make them significant for geometric analysis and real-world applications. Understanding these properties not only expands our knowledge of geometry but also enhances our ability to solve problems and design solutions in various fields.

Perpendicularity of the Lines of Symmetry in a Rectangle

When we talk about perpendicularity, we’re referring to lines [that meet at a 90-degree angle] forming a right angle. In the world of geometry, lines of symmetry play a crucial role in the fascinating world of rectangles. These lines embody a [special relationship] with each other, a relationship defined by perpendicularity.

In a rectangle, its lines of symmetry don’t just happen to intersect; they do so [purposefully], forming right angles. Imagine a rectangle as a perfect canvas. Now, picture two intersecting lines that divide it into four equal parts. These lines are the lines of symmetry. And just like a compass pointing north, these lines maintain their [precise 90-degree angle] where they cross, creating a meeting point that’s the very [heart of the rectangle].

This perpendicularity is not a coincidence. It’s an intrinsic property that stems from the very [definition of a rectangle]. In fact, perpendicularity is one of the key characteristics that distinguishes a rectangle from other quadrilaterals. So, when you encounter a rectangle, remember this secret: its [lines of symmetry are perpendicular by design], adding to the beauty and order of this geometric marvel.

Division into Congruent Right Triangles

Imagine dividing a rectangle into four smaller shapes using its two perpendicular lines of symmetry. These shapes are not just any shapes; they are four congruent right triangles.

Congruence in geometry means that two figures have the same shape and size. In other words, they are identical in every way. So, how do the lines of symmetry create these congruent right triangles?

Each line of symmetry cuts the rectangle into two identical halves. These halves are now two congruent rectangles. Now, recall that a diagonal line drawn from one corner to the opposite corner of a rectangle divides it into two right triangles. So, by drawing the diagonal lines on both halves of the rectangle, we end up with four congruent right triangles.

Here’s the proof:
– The sides adjacent to the right angles, also known as the legs, are equal because they are parts of the same diagonal line.
– The third side, known as the hypotenuse, is also equal because it is a diagonal line connecting opposite corners of the rectangle.
– Since the corresponding legs and hypotenuse are equal in all four triangles, they are considered congruent.