Unveiling The End Behavior Of Rational Functions: A Comprehensive Guide

To find the end behavior of a rational function, determine the degrees of the numerator and denominator to calculate the relative degree. This provides insights into the overall behavior. Consider the leading coefficients to identify upward or downward trends as the variable approaches infinity. Vertical asymptotes are found by setting the denominator to zero, indicating undefined points. Horizontal asymptotes may exist if the numerator and denominator degrees differ. Combine these clues to describe the function’s behavior as the variable approaches positive or negative infinity.

What is end behavior and its significance in analyzing rational functions.

Understanding End Behavior: A Guide to Analyzing Rational Functions

In the realm of mathematics, rational functions play a crucial role in describing the behavior of functions. Their ability to model real-world phenomena makes them indispensable tools for scientists, engineers, and analysts alike. However, to fully grasp their intricacies, we must first delve into the concept of end behavior.

End behavior refers to the characteristics of a function as its input, or independent variable, approaches infinity (either positive or negative). In the case of rational functions, their end behavior is particularly significant because it provides valuable insights into their overall behavior. By understanding how a function behaves at the extremes, we can gain a better understanding of its behavior throughout its entire domain.

The Significance of End Behavior

End behavior is essential for understanding the long-term trends of a rational function. It reveals whether the function has any vertical or horizontal asymptotes, which can divide the coordinate plane into intervals of behavior. Additionally, it helps us predict the function’s values as the input gets larger or smaller, allowing us to make informed decisions based on mathematical models.

Determining End Behavior

The key elements in determining the end behavior of a rational function are the relative degree and the leading coefficients of its numerator and denominator. The relative degree is calculated by subtracting the degree of the denominator from the degree of the numerator. It provides clues about the overall behavior of the function.

The leading coefficients of the numerator and denominator determine whether the function tends towards positive or negative infinity. If both coefficients are positive, the function tends towards positive infinity. If both are negative, the function tends towards negative infinity. If the coefficients have opposite signs, the function tends towards the coefficient with a greater magnitude.

Vertical Asymptotes: Limits of Definition

Vertical asymptotes are lines in the coordinate plane at which a function becomes undefined. They occur when the denominator of a rational function equals zero. At these points, the function approaches infinity or negative infinity, creating vertical gaps in its graph.

Horizontal Asymptotes: Approaching Stability

Horizontal asymptotes are lines in the coordinate plane that the function approaches as the input approaches infinity or negative infinity. They occur when the relative degree of the numerator is less than the relative degree of the denominator. At these points, the function’s values stabilize and approach a constant value.

End Behavior: Combining Insights

By combining the information gathered from the relative degree, leading coefficients, vertical asymptotes, and horizontal asymptotes, we can fully describe the end behavior of a rational function. This knowledge empowers us to analyze the function’s overall behavior and make informed predictions about its values for large or small inputs.

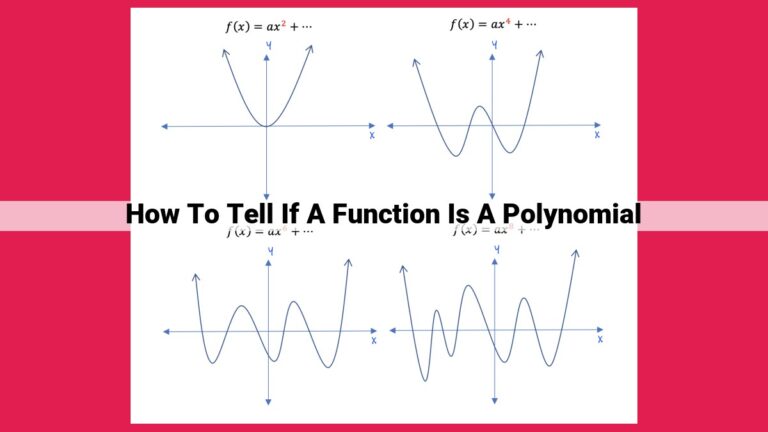
Definition of degree and how to determine it for both numerator and denominator.

Understanding the Degree of Rational Functions: A Journey into Mathematical Patterns

In the realm of rational functions, the degree holds a significant place. It’s like a compass that guides us in unraveling the mysteries of these functions, uncovering hidden patterns in their behavior as they reach towards infinity.

The Tale of Numerator and Denominator Degrees

Just as a house has both a roof and a foundation, a rational function has a numerator and denominator. The degree of each is the highest exponent of the variable they contain. Think of the degree as a measure of the “strength” of these components.

To determine the degree, embark on a simple mathematical expedition. For the numerator, count the highest power of the variable. For example, in the function 2x³ + 5x², the numerator’s degree is 3. Now, repeat the adventure for the denominator. In the function x² – 3x + 2, the denominator’s degree is 2.

The Relative Degree: A Guiding Light

The relative degree of a rational function is like a magic wand that reveals the function’s overall behavior at infinity. It’s calculated by subtracting the denominator’s degree from the numerator’s degree. A positive relative degree indicates that the numerator “outpowers” the denominator, while a negative relative degree suggests the opposite.

The Significance of Leading Coefficients: A Hint of Behavior

Imagine a rational function as a car speeding down an infinite road. The leading coefficients are like the gas pedal and brake, determining the direction and speed of the function as it approaches infinity. A positive leading coefficient indicates an upward trend, while a negative leading coefficient signals a downward trajectory.

Equipped with the knowledge of degree and leading coefficients, we can embark on a captivating journey to uncover the end behavior of rational functions, unraveling the secrets of their mathematical dance towards infinity.

Understanding the End Behavior of Rational Functions

When analyzing rational functions, it’s crucial to grasp their end behavior, which describes how the function behaves as the input variable approaches infinity or negative infinity. This knowledge empowers us to make informed predictions about the function’s overall shape and behavior.

Determining Relative Degree

Relative degree is a key concept in understanding end behavior. It’s calculated by subtracting the degree of the denominator from the degree of the numerator. The degree of a polynomial (numerator or denominator) refers to the highest power of the variable present in that polynomial.

Example

Consider the rational function f(x) = (x^2 – 4) / (x + 2). The degree of the numerator is 2, and the degree of the denominator is 1. Thus, the relative degree of f(x) is 2 – 1 = 1.

Insights from Relative Degree

The relative degree provides valuable clues about the overall behavior of the rational function:

• Positive relative degree (numerator degree greater than denominator degree): The function rises indefinitely as x approaches infinity and negative infinity.
• Negative relative degree (denominator degree greater than numerator degree): The function falls indefinitely as x approaches infinity and negative infinity.
• Zero relative degree (numerator and denominator degrees equal): The function approaches a finite limit as x approaches infinity and negative infinity.

Understanding relative degree is a powerful tool for quickly predicting the end behavior of rational functions.

Dive into the Secrets of Relative Degree: Unlocking the End Behavior of Rational Functions

As you embark on your mathematical adventure, you’ll encounter a fascinating concept called rational functions. They may seem intimidating at first, but with a bit of storytelling magic, we’ll unveil their intriguing secrets.

Let’s imagine a rational function as a see-saw, with the numerator and denominator sitting at opposite ends. The relative degree of a rational function is like the weight difference between these two sides. It’s calculated by subtracting the degree of the denominator from the degree of the numerator.

This relative degree holds a treasure trove of clues about the overall behavior of our function. If the relative degree is positive, it means the numerator has a greater influence than the denominator. As the variable shoots towards infinity or negative infinity, the function will behave like the numerator.

Conversely, if the relative degree is negative, the denominator reigns supreme. As the variable approaches the ends of the number line, the function will mimic the behavior of the denominator.

In simpler terms, a positive relative degree suggests that the function will either rise or fall without bound as the variable approaches infinity. A negative relative degree, on the other hand, implies that the function will approach a horizontal line (called a horizontal asymptote) as the variable gets infinitely large or small.

So, the next time you come across a rational function, don’t just scratch your head. Calculate its relative degree, embrace the storytelling approach, and let it guide you in unraveling the function’s end behavior. It’s like having a secret superpower that unlocks the mysteries of the mathematical world!

Identifying positive or negative leading coefficients and their impact on end behavior.

Significance of Leading Coefficients: Unlocking the Secrets of End Behavior

As we venture deeper into the realm of rational functions, we encounter a pivotal element that profoundly influences their end behavior: leading coefficients. These coefficients, found in the highest-degree terms of the numerator and denominator, hold the key to understanding how the function behaves as the variable approaches infinity.

Positive Leading Coefficients: Upward Trends

When the leading coefficient of the numerator is positive, the function rises as the variable approaches infinity in both the positive and negative directions. This positive trend signifies an upward trajectory, just like a rocket soaring into the sky.

Conversely, a positive leading coefficient in the denominator indicates a downward trend. As the variable approaches infinity, the function dips towards the negative values, similar to a rollercoaster plummeting towards the earth.

Negative Leading Coefficients: Reverse Trends

The story reverses when the leading coefficient of the numerator is negative. In this case, the function decreases as the variable approaches infinity. It’s as if the function is taking a nosedive, rapidly spiraling downwards.

On the other hand, a negative leading coefficient in the denominator represents an upward trend. The function ascends towards positive infinity, mirroring the graceful flight of a bird taking off.

Impact on End Behavior

These leading coefficients, like maestros of the rational function orchestra, orchestrate the function’s end behavior. By analyzing their signs and magnitudes, we can predict the function’s overall trajectory as it stretches towards infinity. This understanding is crucial for sketching graphs and interpreting the function’s behavior in real-world applications.

Understanding the Significance of Leading Coefficients in End Behavior

In the realm of rational functions, the leading coefficients of the numerator and denominator play a pivotal role in determining the function’s end behavior. These coefficients reveal crucial information about the overall trend of the function as the variable approaches infinity.

Imagine a rational function as a roller coaster of values, where the variable is the rider. As the variable moves towards positive infinity (∞), the roller coaster might soar to dizzying heights or plunge into the depths of negative values. Similarly, as the variable approaches negative infinity (-∞), the roller coaster’s trajectory could take a different turn.

The sign of the leading coefficient of the numerator tells us whether the roller coaster is trending upward (positive coefficient) or downward (negative coefficient) as the variable approaches infinity. For example, consider the function f(x) = (x^2 – 4)/(x + 1). The numerator has a positive leading coefficient (1), indicating that the function will rise towards infinity.

Meanwhile, the sign of the leading coefficient of the denominator determines the direction of the roller coaster’s descent towards infinity. A positive coefficient suggests that the function will approach negative infinity, while a negative coefficient implies that it will diverge away from negative infinity. In our example, the denominator has a positive leading coefficient (1), so the function will approach negative infinity.

Remember, the leading coefficients provide valuable clues about the function’s end behavior. By understanding their significance, we can gain insights into how the function behaves at the ends of its domain, allowing us to unravel the mysteries of its roller coaster ride.

Vertical Asymptotes: Gateways to Infinity

In the realm of rational functions, vertical asymptotes emerge as barriers that the function cannot cross. These boundaries arise from the abyss of zero—when the denominator of our rational function plunges into this forbidden zone.

Just like Alice tumbling down the rabbit hole, our function experiences a sudden drop at these vertical chasms. As the variable approaches the asymptote from the left or right, the function zooms towards positive or negative infinity. It’s as if the function is trying to reach a destination beyond our comprehension, but the asymptote acts as an unpassable barrier.

To find these vertical gatekeepers, we must unveil the secrets within the denominator. By equating it to zero, we uncover the hidden values that make our function undefined. These values mark the points on the x-axis where the function experiences a dramatic leap.

These vertical asymptotes partition the number line into distinct regions. On one side of the asymptote, the function ascends towards infinity like an ambitious climber scaling a mountain. On the other side, it descends into the depths of negative infinity, as if it were plummeting into an unfathomable abyss.

Understanding vertical asymptotes is crucial for navigating the intricate landscape of rational functions. They reveal the boundaries beyond which the function cannot tread, providing valuable insights into its overall behavior.

Vertical Asymptotes: The Gatekeepers of Infinity

In the realm of rational functions, vertical asymptotes stand as formidable barricades, guarding the pathways to infinity. These lines emerge whenever the denominator of a rational function vanishes, indicating a point where the function is undefined.

Like mythical sirens luring sailors to their doom, vertical asymptotes attract the function, drawing it ever closer as the variable approaches their treacherous presence. As the function approaches an asymptote, its magnitude spirals toward infinity, becoming either impossibly large or small.

These asymptotes reveal a function’s hidden potential. By studying their locations, we can deduce the function’s behavior as it navigates the treacherous waters of infinity. For if a function approaches infinity along a vertical asymptote, it does so with boundless determination, never crossing the line that bars its path.

Horizontal Asymptotes: Guiding the Function’s Limit

As we explore the end behavior of a rational function, we encounter horizontal asymptotes, the invisible lines that the function approaches as the input variable tends to infinity. These asymptotes provide crucial insights into the function’s behavior and overall shape.

Determining the existence of a horizontal asymptote hinges on comparing the degrees of the numerator and denominator.

• If the numerator’s degree is lower than the denominator’s degree, the rational function has a horizontal asymptote at y = 0. This is because the denominator’s influence becomes dominant as the variable grows, causing the function to trend towards the horizontal axis (y-axis).

• Conversely, if the numerator’s degree is equal to the denominator’s degree, the horizontal asymptote exists at a non-zero value. We determine this value by dividing the leading coefficients of the numerator and denominator. For instance, if the rational function is (2x + 3)/(x + 1), the leading coefficients are 2 and 1, respectively, so the horizontal asymptote is at y = 2.

Understanding horizontal asymptotes is essential for graphing rational functions. They help us identify the function’s limiting behavior as the variable approaches infinity. These asymptotes provide a visual cue that helps us sketch the function’s shape accurately, allowing us to better visualize its behavior.

Horizontal Asymptotes: Unraveling the Path to Stability

When it comes to rational functions, the dance of degrees between the numerator and denominator holds the key to unraveling their end behavior. One crucial element in this dance is the concept of horizontal asymptotes – magical lines that guide the function’s journey as it ventures out to infinity.

Imagine a roller coaster, careening along its tracks. As it approaches the end of its thrilling ride, it gradually flattens out, settling into a steady glide. Just as the roller coaster finds its rhythm, a rational function also finds its path to stability as it approaches infinity, hovering around a horizontal line.

The existence of a horizontal asymptote depends on a simple battle of degrees. If the degree of the numerator is less than the degree of the denominator, the rational function humbles itself, becoming asymptotically horizontal. As the variable rockets towards positive or negative infinity, the function smoothly approaches this horizontal line, like an asymptote that dances just out of reach, guiding its path.

In other words, the horizontal asymptote represents the value that the function yearns to approach as it journeys to infinity. It mirrors the ratio of the leading coefficients of the numerator and denominator, indicating the function’s ultimate trajectory.

Unveiling the End Behavior of Rational Functions: A Journey of Insights

As we embark on our quest to unravel the mysteries of rational functions, let’s delve into the realm of end behavior – a crucial element in comprehending the overall trajectory of these functions. End behavior offers invaluable clues about how a rational function behaves at both positive and negative infinity.

Combining Relative Degrees and Leading Coefficients: Illuminating the Way

To determine the end behavior of a rational function effectively, we must weave together two essential pieces of information: relative degree and leading coefficients.

Relative Degree: This concept stems from the difference between the degrees of the numerator and denominator. If the numerator’s degree is greater, the rational function will behave as a polynomial with the same degree as the numerator. Conversely, if the denominator’s degree is greater, the function will behave as a horizontal line whose y-intercept is determined by the ratio of the leading coefficients.

Leading Coefficients: These coefficients preside over the terms with the highest powers in the numerator and denominator. They dictate the direction of the function’s end behavior. Positive coefficients indicate that the function will rise as x approaches infinity, while negative coefficients signal a descent.

Unveiling the Function’s Final Act: End Behavior

By harmoniously blending relative degrees and leading coefficients, we can discern the function’s end behavior. Here’s how:

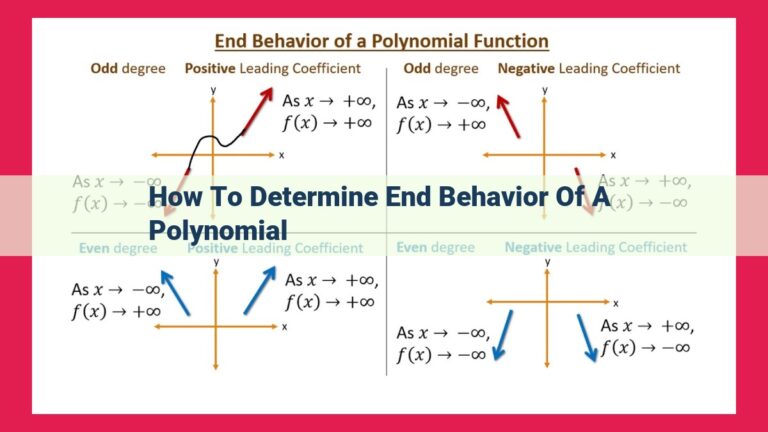
• Positive Relative Degree and Positive Leading Coefficient: The function behaves like a polynomial, rising indefinitely as x approaches both positive and negative infinity.
• Positive Relative Degree and Negative Leading Coefficient: The function behaves like a polynomial, dropping without bound as x approaches both positive and negative infinity.
• Negative Relative Degree and Positive Leading Coefficient: The function approaches a horizontal asymptote as x approaches both positive and negative infinity. The asymptote’s y-coordinate is determined by the ratio of the leading coefficients.
• Negative Relative Degree and Negative Leading Coefficient: The function approaches a horizontal asymptote as x approaches both positive and negative infinity. The asymptote’s y-coordinate is determined by the ratio of the leading coefficients.

Remember: End behavior only describes the function’s behavior at extreme values of x. It does not provide a complete picture of the function’s entire graph.

End Behavior of Rational Functions: Decoding the Asymptotic Symphony

When studying rational functions, delving into their end behavior is crucial. Imagine a function as a musical note resonating in the vast expanse of infinity. As the variable gallops towards infinity, the function’s behavior unveils essential characteristics.

Unraveling the end behavior of a rational function is like deciphering the symphony of its Asymptotic dance. Join us as we embark on this harmonic journey, unraveling the secrets of rational functions and their asymptotic partners.

The first step in this harmonic excursion is to determine the relative degree of the function. Think of the relative degree as the difference between the degrees of the numerator and denominator. This tiny but mighty number holds the key to the function’s overall disposition as the variable waltzes towards infinity.

Next, let’s shed light on the leading coefficients, the conductors of the asymptotic ensemble. These coefficients determine the function’s directional sway as the variable approaches infinity. Picture the function as a graceful ballerina, executing an upward pirouette if the leading coefficients are positive and a downward spiral if they’re negative.

Armed with the knowledge of relative degree and leading coefficients, we can now predict the vertical asymptotes, the vertical boundaries where the function reaches for the celestial heights of infinity. These asymptotes emerge when the denominator serenades the zero mark, creating a divide by zero waltz that sends the function soaring.

But hold on, there’s another Asymptotic dance move to master—the horizontal asymptote. This enchanting line represents the function’s unwavering approach as the variable gallops towards infinity. It appears when the relative degree is zero, indicating that the function dances along a horizontal plane.

Finally, we culminate our Asymptotic symphony by combining all the elements we’ve uncovered. This orchestrated ensemble of relative degree, leading coefficients, vertical asymptotes, and horizontal asymptotes unveils the function’s end behavior. As the variable embarks on its infinite journey, we can now confidently predict its graceful ascent or descent.

So embark on this harmonic adventure, decoding the end behavior of rational functions. Uncover their Asymptotic secrets and revel in the beauty of their mathematical symphony.

Finding the End Behavior of Rational Functions: A Step-by-Step Guide

Rational functions, those that involve polynomials in both the numerator and denominator, can exhibit unique behaviors as the independent variable approaches infinity. End behavior refers to how the function approaches these infinite values and provides valuable insights into its overall shape and characteristics.

Step 1: Determine Degrees of Numerator and Denominator

The degree of a polynomial represents the highest exponent of the independent variable. For rational functions, we calculate the relative degree by subtracting the degree of the denominator from the degree of the numerator.

Step 2: Calculate Relative Degree

The relative degree provides clues about the function’s behavior:

• Positive relative degree: The function approaches infinity or negative infinity at a faster rate than a linear function (y = x).
• Negative relative degree: The function approaches a finite value (horizontal asymptote) at a slower rate than a linear function.
• Zero relative degree: The function has a linear end behavior.

Step 3: Identify Leading Coefficients

The leading coefficient is the coefficient of the highest degree term. Positive leading coefficients indicate upward end behavior, while negative leading coefficients indicate downward end behavior.

Step 4: Find Vertical Asymptotes

Vertical asymptotes are vertical lines where the function is undefined because the denominator is zero. Find these by setting the denominator equal to zero and solving for the variable.

Step 5: Check for Horizontal Asymptotes

Horizontal asymptotes are horizontal lines that the function approaches as the variable goes to infinity. To check for these, compare the degrees of the numerator and denominator:

• Numerator degree < denominator degree: There is a horizontal asymptote at y = 0.
• Numerator degree = denominator degree: There may or may not be a horizontal asymptote. Calculate the ratio of the leading coefficients to determine it.
• Numerator degree > denominator degree: There is no horizontal asymptote.

Step 6: Combine Information for End Behavior

Combine the information from the previous steps to describe the function’s end behavior as the variable approaches positive or negative infinity. For example:

• Positive relative degree, positive leading coefficient: The function increases without bound at both positive and negative infinity.
• Negative relative degree, negative leading coefficient: The function decreases without bound at both positive and negative infinity.
• Zero relative degree, positive leading coefficient: The function approaches a horizontal asymptote at y = 0 and increases without bound at positive infinity.

Determine degrees of numerator and denominator.

Unlocking the Secrets of Rational Functions: A Comprehensive Guide to End Behavior

Imagine embarking on a journey to decipher the enigmatic end behavior of rational functions. Like a detective unraveling a mystery, we’ll delve into the clues that guide us towards understanding their ultimate destiny as the variable approaches infinity.

Determining the Guiding Light: Degree of Numerator and Denominator

The first step in our quest is to determine the degree of both the numerator and denominator. The degree represents the highest power of the variable in each polynomial expression. Just like a ladder has rungs, a polynomial has terms with different degrees. The highest rung, or degree, is the one with the greatest exponent.

Calculating Relative Degree: A Tale of Subtraction

Now, it’s time for a bit of subtraction. We calculate the relative degree by subtracting the degree of the denominator from the degree of the numerator. This simple arithmetic operation will give us valuable insights into the function’s overall behavior.

Positive or Negative: The Significance of Leading Coefficients

Just as a compass points north or south, the leading coefficient, the coefficient of the highest degree term, holds a special significance. A positive leading coefficient indicates that the function will trend upwards as the variable approaches infinity, while a negative leading coefficient signals a downward trajectory.

Vertical Asymptotes: Defining Boundaries

Vertical asymptotes are like invisible walls that the function cannot cross. They occur at points where the denominator equals zero, causing the function to become undefined and shoot off to infinity like a rocket. Understanding these asymptotes is crucial for grasping how the function behaves.

Horizontal Asymptotes: Approaching Stability

In contrast to vertical asymptotes, horizontal asymptotes represent a stable equilibrium. They indicate the horizontal line that the function tends to approach as the variable approaches infinity. We can identify them by comparing the degrees of the numerator and denominator.

Combining Clues for End Behavior: A Symphony of Insights

Now, it’s time to combine all the clues we’ve gathered. Relative degrees, leading coefficients, vertical asymptotes, and horizontal asymptotes work together like a symphony, revealing the end behavior of the rational function. We can describe how the function behaves as the variable approaches positive or negative infinity, unlocking a deeper understanding of its nature.

Exploring the End Behavior of Rational Functions

In the realm of algebra, rational functions hold a special place. They are fractions of two polynomials, and their behavior can be quite complex. However, by understanding their end behavior, we can gain valuable insights into their overall nature.

One crucial aspect in determining end behavior is the degree of the numerator and denominator. The degree of a polynomial is the highest exponent of the variable it contains. In a rational function, the relative degree becomes paramount.

Relative Degree: A Guiding Clue

Relative degree is the difference between the degree of the numerator and denominator. It provides us with a sneak peek into the function’s behavior as the variable becomes infinitely large.

• If the relative degree is positive, the numerator’s growth outpaces the denominator’s, leading to an infinite value for the function.
• If the relative degree is negative, the denominator’s growth dominates, causing the function to approach zero as the variable approaches infinity.

Leading Coefficients: The Pillars of End Behavior

The leading coefficients of the numerator and denominator play a vital role in determining the end behavior. These coefficients are the coefficients of the terms with the highest degrees.

• A positive leading coefficient indicates that the function will trend upward as the variable approaches infinity, while a negative leading coefficient suggests a downward trend.
• The larger the magnitude of the leading coefficient, the steeper the function’s slope as it approaches infinity.

Understanding End Behavior of Rational Functions: A Journey into Mathematical Insight

In the realm of mathematics, rational functions hold a special place, offering a glimpse into the behavior of complex expressions as they approach infinity. Understanding their end behavior is crucial for unraveling their characteristics and unraveling their secrets.

Embarking on this journey, we will uncover the significance of leading coefficients, the guiding force behind a rational function’s trajectory as it ventures toward infinity.

Positive Leading Coefficients: An Upward Soar

When the leading coefficient of the numerator and denominator carry a positive sign, the function takes on an optimistic disposition. As the variable approaches positive infinity, the function soars upward, stretching to reach ever-higher values. This is akin to tracing an invisible staircase that ascends without bounds.

Conversely, if the leading coefficient of the denominator eclipses that of the numerator, the function faces negative infinity. The function takes on a downward plunge, descending deeper and deeper into the abyss as the variable increases without limit.

Negative Leading Coefficients: A Downward Dive

Now, let’s consider the scenario where the leading coefficient of the numerator is negative. This reversal of fortune sets the function on a downward spiral as the variable approaches positive infinity. The function descends into negative territory, reaching ever-lower depths.

However, if the leading coefficient of the denominator outweighs that of the numerator, the function defies the downward trend. Instead, it ascends toward positive infinity, albeit with a more measured pace than its positive counterpart.

The Symphony of Coefficients: A Dance of Trends

These leading coefficients act as silent conductors, orchestrating the function’s end behavior. Their interplay creates a dynamic choreography that determines whether the function soars or sinks as the variable reaches for infinity.

By grasping the significance of leading coefficients, we gain a profound understanding of the asymptotic behavior of rational functions, enabling us to predict their trajectories and unravel their mathematical tapestry.

Demystifying the Anatomy of Rational Functions: A Journey to Uncover End Behavior

In the realm of mathematics, rational functions are fascinating curves that dance across the coordinate plane, revealing valuable insights into the behavior of numbers. These functions are constructed using fractions of polynomials, lending them unique characteristics that we’re about to explore. Join us as we embark on a voyage to unveil the secrets behind the end behavior of rational functions, a crucial aspect that governs their asymptotic destinations as they venture toward infinity.

Understanding End Behavior: A Compass for Navigating Rational Functions

Before delving into the specifics, let’s lay the foundation by defining end behavior. It refers to the pattern exhibited by a function as the input variable approaches positive or negative infinity. By studying end behavior, we gain a comprehensive understanding of the overall shape and tendencies of rational functions.

A Tale of Degrees: Numerator and Denominator

Every rational function is composed of two polynomials: the numerator and the denominator. The degree of a polynomial represents its highest exponent, indicating its complexity. For clarity, let’s break down the degrees of the numerator and denominator into separate concepts.

Numerator Degree: This value discloses the number of times the variable is multiplied by itself in the numerator.

Denominator Degree: Similarly, it conveys the number of times the variable is multiplied by itself in the denominator.

Relative Degree: A Guide to Asymptotic Insights

To unravel the mysteries of end behavior, we introduce the concept of relative degree, which is calculated by subtracting the denominator degree from the numerator degree. This pivotal value provides valuable clues about the function’s overall behavior.

Positive Relative Degree: When the numerator degree exceeds the denominator degree, the function tends to infinity as the variable approaches both positive and negative infinity. Imagine a roller coaster that never quite reaches the ground, perpetually soaring to greater heights.

Negative Relative Degree: Conversely, if the denominator degree dominates, the function tends to zero as the variable approaches both ends of the spectrum. Picture a gentle slope that slowly fades into oblivion, reaching the origin as its ultimate destination.

Zero Relative Degree: In this case, the numerator and denominator degrees are in harmony, indicating that the function approaches a specific non-zero value as the variable travels toward infinity. It’s like a determined traveler who eventually settles into a steady rhythm, maintaining a constant pace toward a known destination.

The Significance of Leading Coefficients: A Vote for Upward or Downward Trends

Leading coefficients play a crucial role in shaping the end behavior of rational functions. These coefficients are the non-zero coefficients multiplying the highest powers of the variable in the numerator and denominator.

Positive Leading Coefficient: When the numerator’s leading coefficient is positive, the function rises as the variable approaches infinity. Picture a sailboat gracefully gliding upward, its sails catching the wind and propelling it toward the heavens.

Negative Leading Coefficient: On the other hand, a negative numerator coefficient causes the function to descend as the variable ventures toward infinity. Imagine a rollercoaster plunging downward, its momentum carrying it toward the earth’s embrace.

Understanding the End Behavior of Rational Functions

In the realm of rational functions, understanding their end behavior is crucial. It provides us with insights into how the function behaves as the input approaches infinity or negative infinity. To decipher this behavior, we’ll embark on a journey through the key concepts that shape its end behavior.

Degree of Numerator and Denominator: The Foundation

The degree of a rational function is determined by the highest power of the variable in the numerator and the denominator. The numerator degree represents the polynomial’s overall strength, while the denominator degree indicates its complexity.

Relative Degree: A Glimpse into Behavior

By subtracting the denominator degree from the numerator degree, we obtain the relative degree. This value tells us the overall direction of the function as the input approaches infinity. A positive relative degree implies upward movement, while a negative relative degree indicates a downward trend.

Significance of Leading Coefficients: Guiding the Asymptotes

The leading coefficients of the numerator and denominator play a pivotal role in shaping the end behavior. They determine whether the function tends towards positive or negative infinity as the input approaches infinity. Positive leading coefficients indicate upward movement, while negative leading coefficients signal a downward trajectory.

Vertical Asymptotes: Infinite Divides

Vertical asymptotes are vertical lines at which the function is undefined due to division by zero. They occur when the denominator of the rational function equals zero. At these lines, the function approaches infinity either positively or negatively, creating a vertical divide in the graph.

Horizontal Asymptotes: A Destination to Infinity

In some cases, a rational function may approach a stable horizontal line as the input approaches infinity. This is known as a horizontal asymptote. It is determined by comparing the degrees of the numerator and denominator. When the numerator degree is less than the denominator degree, a horizontal asymptote exists, representing the function’s ultimate destination as it stretches towards infinity.

Understanding End Behavior: Unlocking the Mysteries of Rational Functions

In the realm of functions, rational functions stand apart, characterized by their ability to express a fraction of two polynomials. To fully comprehend their behavior, unraveling their end behavior is crucial. It provides insights into how they behave at the extremes of their domain—as the input variable approaches infinity or negative infinity.

At the heart of end behavior lies the relative degree, determined by subtracting the denominator’s degree from the numerator’s degree. This enigmatic number holds the key to understanding the function’s overall sway. A positive relative degree foretells an upward trajectory, while a negative relative degree heralds a downward path.

Like the yin and yang of mathematics, leading coefficients play a pivotal role in end behavior. A positive leading coefficient in the numerator signals a harmonious upward ascent, while a negative one warns of a downward descent.

Vertical asymptotes emerge as the boundary lines where the function’s denominator vanishes. These celestial lines mark the territories where the function approaches infinity, yielding undefined points.

In contrast, horizontal asymptotes serve as a steady horizon, indicating the function’s approach to a stable value as the variable approaches infinity. They arise when the numerator’s degree is equal to or less than the denominator’s.

By deftly combining these clues, we can unmask the end behavior of any rational function. A positive relative degree and a positive leading coefficient paint a picture of an upward surge, while a negative relative degree and a negative leading coefficient depict a downward plunge.

End Behavior: A Practical Guide

To decode the end behavior of a rational function, embark on this step-by-step adventure:

1. Unveil the degrees of numerator and denominator: These celestial bodies reveal the function’s underlying structure.
2. Calculate the relative degree: Subtract the denominator’s degree from the numerator’s—an enchanting number that holds the key to overall behavior.
3. Identify leading coefficients: Positive or negative, these coefficients dictate the function’s ultimate destiny.
4. Find vertical asymptotes: Set the denominator to zero and witness the emergence of these forbidden territories.
5. Check for horizontal asymptotes: Determine if the numerator’s degree is equal to or less than the denominator’s to uncover potential stabilizing forces.
6. Combine information for end behavior: Synthesize all the gathered insights to unravel the function’s behavior at the ends of its domain.