Understanding Holes In Rational Functions: A Concise Guide For Optimization

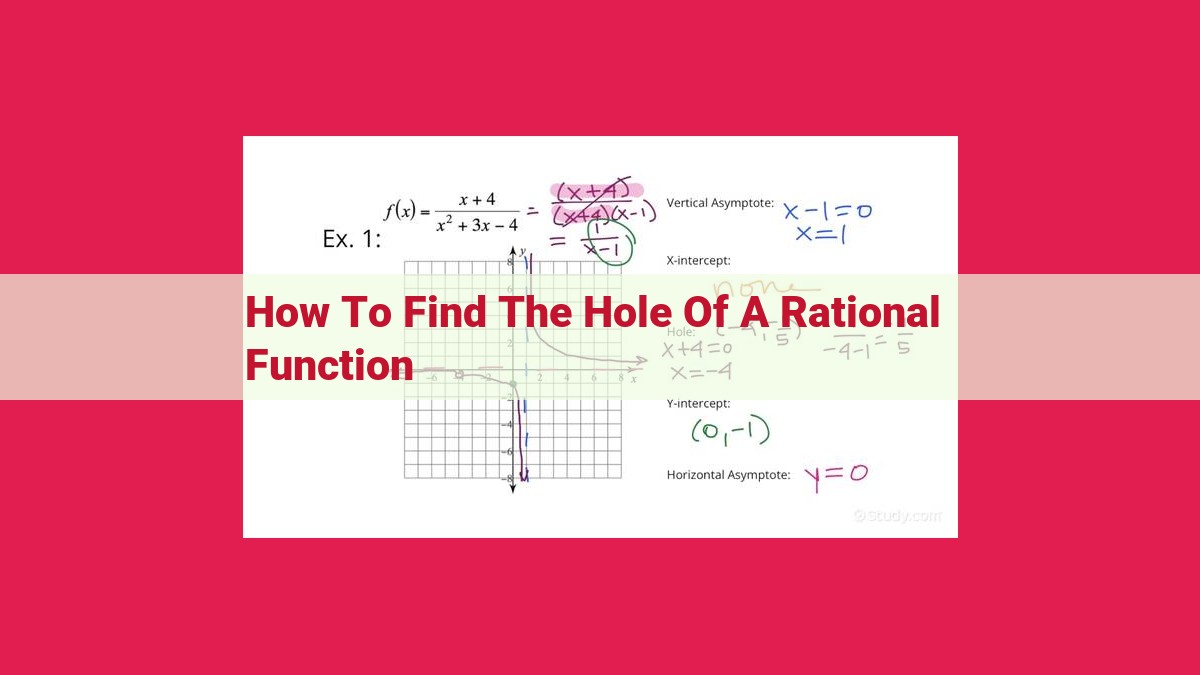
To find the hole of a rational function, factor the function and identify any undefined points (points where the denominator is 0). Then, check if any factors cancel out without creating asymptotes. If they do, the point is a hole. Holes are distinct from non-holes because they occur when factors cancel out, resulting in a removable discontinuity. Unlike vertical asymptotes, which indicate an undefined point, holes are filled by extending the function to the undefined point.

Unveiling the Secrets of Rational Functions: Asymptotes, Holes, and Beyond

In the captivating world of mathematics, rational functions stand out as functions that can be expressed as the quotient of two polynomials. Understanding the intricacies of these functions is crucial for unraveling their behavior and unlocking their mathematical secrets. Let’s embark on a journey to explore the key concepts that govern rational functions: asymptotes, holes, factors, zeros, and more.

Understanding Key Concepts

1. Asymptotes: Asymptotes are lines that the graph of a function approaches as the input or output values increase or decrease without bound.

2. Holes: Holes are points on the graph of a function where the function is undefined. They occur due to the cancellation of factors in the numerator and denominator of the function.

3. Factors: Factors are the individual polynomials that, when multiplied together, form the numerator or denominator of a rational function.

4. Rational Functions: Rational functions are functions that can be expressed as the quotient of two polynomials, where the denominator is not zero.

5. Zeros: Zeros are the values of the input variable for which the function equals zero. They correspond to the points where the graph of the function crosses the x-axis.

Identifying Holes in Rational Functions: A Step-by-Step Guide

In the realm of mathematics, rational functions are functions that can be expressed as a ratio of two polynomials. While they may seem complex at first, understanding the concept of holes in rational functions is crucial for mastering this topic.

The Step-by-Step Process

Identifying holes in rational functions involves a systematic process that can be broken down into several key steps:

1. Factoring the Function: Begin by factoring the numerator and denominator of the rational function into their prime factors. This will help you identify potential holes.

2. Identifying Undefined Points: Look for any factors in the denominator that make it equal to zero. These values are called undefined points because they make the function undefined.

3. Avoiding Undefined Points: To avoid these undefined points, cancel out any common factors between the numerator and denominator that share the same undefined point.

4. Checking for Cancellation: After canceling common factors, check whether the resulting function is still undefined at any points. If it is, the function has a hole at that point.

Relationship between Holes and Asymptotes

It’s important to note that holes in rational functions can occur in the presence of vertical asymptotes. Vertical asymptotes represent points of discontinuity where the function becomes infinite.

On the other hand, horizontal asymptotes represent limits that the function approaches as [x] approaches infinity or negative infinity. Holes can occur at the same points as vertical asymptotes but are distinct from them.

Distinguishing Holes from Non-Holes

It’s essential to distinguish between holes and non-holes in rational functions. Holes occur when factors in the numerator and denominator cancel out without creating an asymptote.

Non-holes, on the other hand, occur when there are no undefined points or when common factors cannot be canceled without creating an asymptote.

Asymptotes and Holes: A Deeper Dive

Understanding the Asymptotic Landscape

As we delve into the world of rational functions, we encounter two distinct types of asymptotes: vertical and horizontal. Vertical asymptotes emerge at points where the function becomes undefined, while horizontal asymptotes serve as horizontal boundaries the function approaches as it extends towards infinity.

The Interplay of Asymptotes and Holes

One crucial distinction to make is the difference between asymptotes and holes. While both occur at points where the function is undefined, holes arise when a common factor cancels out between the numerator and denominator. This cancellation, unlike the creation of an asymptote, results in a removable discontinuity, where the function can be redefined to remove the hole.

Distinguishing Holes from Asymptotes

To differentiate between holes and asymptotes, we must examine the behavior of the function at the undefined point. If the cancellation of factors creates a hole, the function approaches a finite value as it gets arbitrarily close to the undefined point. This finite value represents the location of the hole.

On the other hand, if the cancellation of factors leaves behind an undefined expression, it indicates the presence of a vertical asymptote. In this case, the function either increases or decreases without bound as it approaches the undefined point, creating a vertical line that the function cannot cross.

Identifying Holes in Rational Functions

In the realm of mathematics, rational functions hold a special place. They are constructed from quotients of polynomials, giving rise to unique behaviors that can be understood through the concepts of holes and asymptotes.

Holes: Absence of Undefined Points

Holes represent points where a rational function is undefined, but they differ from asymptotes in a crucial way. When you factor a rational function and identify undefined points, the function can be rewritten to avoid these points. This process of cancellation results in holes.

Non-Holes: Asymptotic Boundaries

In contrast to holes, asymptotes indicate points where the function approaches infinity. They cannot be removed by cancellation and serve as boundary lines that the function cannot cross. Vertical asymptotes occur at undefined points, while horizontal asymptotes indicate the function’s behavior as it approaches infinity.

Distinguishing Holes from Non-Holes: A Closer Look

To differentiate between holes and non-holes, consider the following example:

f(x) = (x-2)/(x-1)

Factoring the denominator reveals an undefined point at x = 1. However, cancellation can be performed to obtain:

f(x) = (x-2)/(x-1) = 1 / (1-x)

The resulting function has no undefined point at x = 1, indicating the presence of a hole at that point.

Holes and asymptotes provide valuable insights into the behavior of rational functions. Holes represent points where the function is undefined, but can be removed through cancellation. Asymptotes, on the other hand, are boundary lines that the function cannot cross. Understanding these concepts is essential for analyzing and interpreting rational functions effectively.