Quantify Uncertainty: Confidence Intervals In Statistics

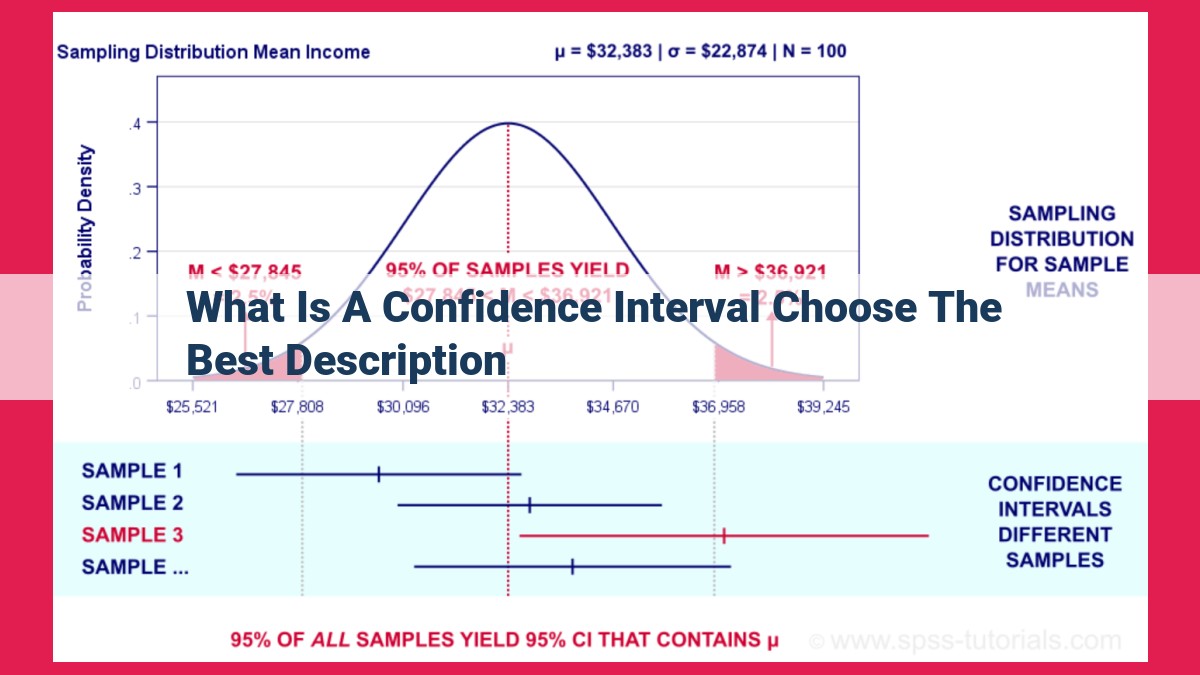
A confidence interval is a range of values that is likely to include the true value of a population parameter based on sample data. It is constructed using a sample statistic, a margin of error, and a confidence level, which represents the probability that the interval will capture the true parameter. The margin of error is half the width of the interval and is affected by the confidence level and sample size, with a wider interval or smaller sample producing a larger margin of error. By understanding these concepts, researchers can construct accurate confidence intervals to quantify the uncertainty associated with population parameters.

What is a Confidence Interval?

In the realm of statistics, confidence intervals are essential to quantify the uncertainty associated with population parameters based on sample estimates. We encounter the term “population” a lot in statistics, but what does it mean? Think of it as the vast collection of data representing an entire group you wish to study. However, it’s often impractical to gather information from every single individual in that population. That’s where samples come in. They’re a bite-sized representation of the population that we can feasibly collect data from.

Now, back to confidence intervals. They’re like virtual boundaries constructed around a sample statistic, providing a range of plausible values within which we can expect to find the true population parameter. It’s not a guarantee that the true value lies within this interval, but it’s highly probable, as determined by our chosen confidence level.

Sampling Error and Population Parameters

In the realm of statistics, we often deal with the challenge of making inferences about a larger population based on a smaller sample. This is where the concept of sampling error comes into play. It refers to the difference between an observed value calculated from a sample and the true value within the population from which the sample was drawn.

Understanding population parameters is crucial for comprehending sampling error. A population parameter is a numerical characteristic that describes a property of the entire population. For instance, the average height of a population is a population parameter. When we calculate a sample statistic, such as the average height of a group of individuals, it may deviate from the true population parameter due to random fluctuations in the sample selection.

The statistical significance threshold is a concept that helps us determine if a discrepancy between a sample statistic and a population parameter is statistically meaningful. It represents the probability of observing a difference as extreme or more extreme than the one we obtained, assuming the null hypothesis (that there is no difference) is true. If the probability falls below a predetermined threshold (usually 0.05), we conclude that the difference is statistically significant and reject the null hypothesis.

Confidence Level and Probability: Understanding the Certainty in Your Findings

In the realm of statistics, confidence intervals play a crucial role in quantifying the uncertainty associated with population parameters. These intervals provide a range of plausible values within which the true population parameter is likely to lie. Understanding the concepts of confidence level and probability is essential for interpreting and constructing accurate confidence intervals.

A confidence level is a percentage that represents the probability that a confidence interval will capture the true population parameter. This means that if you were to repeatedly sample from the same population and construct confidence intervals for each, approximately the specified percentage of those intervals would contain the true population parameter.

The choice of confidence level depends on the desired accuracy and significance of your findings. A higher confidence level means a narrower margin of error (the half-width of the confidence interval) and a greater likelihood of capturing the true population parameter. However, this comes at the cost of reduced statistical significance.

Conversely, a lower confidence level results in a wider margin of error and a reduced probability of including the true population parameter. This increased margin of error allows for greater statistical significance, as it encompasses a wider range of potential values.

Selecting an appropriate confidence level requires balancing the trade-off between accuracy and significance. For instance, in medical research, a higher confidence level may be preferred to ensure greater certainty in treatment recommendations, while in social science research, a lower confidence level may be acceptable to allow for greater statistical power and sensitivity to detect differences.

Margin of Error and Confidence Intervals

In the realm of statistics, confidence intervals provide a range of values that have a specified probability of encompassing the true population parameter. The margin of error plays a crucial role in determining the width of this range.

The margin of error is simply half the width of the confidence interval. It represents the maximum distance the interval’s endpoints can be from the true population parameter. This margin is directly influenced by two key factors:

• Confidence Level: A higher confidence level results in a wider margin of error. This is because a higher confidence level requires a larger probability that the interval contains the true parameter. As the probability increases, the interval must expand to capture more potential values.

• Sample Size: A smaller sample size also leads to a wider margin of error. This is because a smaller sample provides less information about the population. Consequently, the confidence interval must be widened to account for the increased uncertainty.

The relationship between confidence level, sample size, and margin of error can be summarized as follows:

Wider Confidence Level or Smaller Sample Size → Wider Margin of Error

In other words, if you want to have a higher level of confidence in your interval or if you only have a limited sample size, expect a wider margin of error. Conversely, if you are willing to accept a lower confidence level or have a larger sample size, the margin of error will be narrower.

Understanding the margin of error is crucial for interpreting confidence intervals correctly. It provides a measure of the precision of the interval and helps you determine the potential range of the true population parameter.

Constructing a Confidence Interval: A Step-by-Step Guide

Imagine you’re a curious researcher wanting to know the average height of a particular population. You can’t measure everyone, so you collect data from a representative sample. But how sure can you be that your sample accurately represents the entire population? That’s where confidence intervals come in.

Formula: Confidence Interval = Sample Statistic ± Margin of Error

To construct a confidence interval, you need the sample statistic (e.g., sample mean), confidence level (e.g., 95%), and the margin of error.

Step 1: Determine the Margin of Error

The margin of error is determined by the confidence level and the sample size. A higher confidence level or a smaller sample size results in a wider margin of error. The formula for the margin of error varies depending on the distribution of the data.

Step 2: Calculate the Confidence Interval

Once you have the margin of error, you can calculate the confidence interval using the formula:

Confidence Interval = Sample Statistic ± Margin of Error

For example, if you have a sample mean of 1.5 with a margin of error of 0.2, the 95% confidence interval would be:

1.5 ± 0.2 = (1.3, 1.7)

Example: Estimating Population Height

Let’s say you measure the heights of 100 individuals and find an average height of 5 feet 10 inches. You want to construct a 95% confidence interval for the population mean height.

• Sample Statistic: 5 feet 10 inches (5.8 feet)
• Confidence Level: 95%
• Margin of Error: 0.2 feet (determined using statistical tables)

Using the formula, we get:

Confidence Interval = 5.8 ± 0.2 = (5.6, 6.0)

Therefore, we can be 95% confident that the true mean height of the population lies between 5 feet 6 inches and 6 feet.