Understanding Quadrilaterals: Classification And Geometric Properties

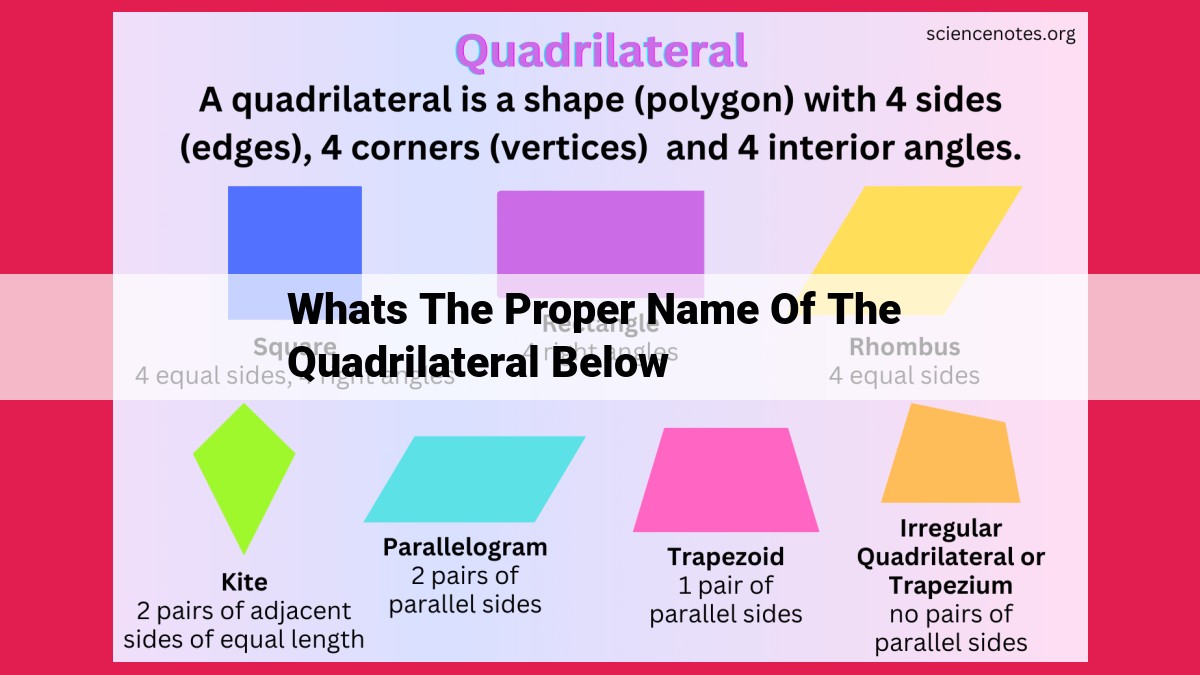
Quadrilaterals are closed shapes with four sides and four angles. Different types of quadrilaterals exist based on their specific properties. Rectangles, parallelograms, rhombuses, and squares have parallel sides and opposite angles equal. Trapezoids have one pair of parallel sides. Kites have two distinct pairs of adjacent sides of equal length. Deltoids have all sides of equal length. Proper identification of the quadrilateral type is crucial for accurate geometrical problem-solving and understanding its specific characteristics.

Quadrilaterals: A Comprehensive Guide to Understanding and Identifying These Basic Shapes

In the realm of geometry, quadrilaterals hold a special place as the fundamental building blocks of many complex shapes and structures. These four-sided polygons, with their varied forms and properties, play a crucial role in shaping our visual world. Delving into their complexities can enhance our understanding of geometry and equip us for various mathematical endeavors.

Defining Quadrilaterals: A Foundation of Knowledge

Quadrilaterals, as their name suggests, are polygons with four sides and four vertices. These versatile shapes can assume diverse forms, each with its distinct characteristics and properties. Their common feature is the presence of four sides that join at the vertices, forming a closed figure. This basic definition serves as the foundation for exploring the diverse landscape of quadrilaterals.

Exploring the Quadrilateral Spectrum: A Journey into Variety

The world of quadrilaterals is a diverse tapestry of shapes with varying attributes. Among the most prominent are rectangles, known for their four right angles and opposite sides of equal length. Their orthogonal nature makes them ideal for creating orderly and structured designs. Closely related to rectangles are parallelograms, which share the property of opposite sides being parallel. However, parallelograms do not necessarily have right angles, giving them a more versatile appearance.

Delving into Quadrilateral Subtypes: Unveiling Unique Properties

The quadrilateral family extends beyond rectangles and parallelograms, encompassing a rich diversity of shapes. Rhombuses, for instance, are parallelograms with all sides equal, giving them a distinctive diamond-like appearance. Squares, a special case of rhombuses, possess equal sides and four right angles, making them the epitome of symmetry and order.

Moving beyond these familiar forms, we encounter trapezoids, characterized by one pair of parallel sides. Their distinctive shape makes them useful for creating sloped surfaces and irregular designs. Kites are another intriguing subtype, boasting two pairs of adjacent sides of equal length, resulting in a shape resembling a diamond with a tail. Lastly, deltoids, also known as kites with no right angles, exhibit a distinctive triangle-like shape with three sides of equal length.

Classifying Quadrilaterals: A Step-by-Step Approach

Navigating the diverse realm of quadrilaterals requires a systematic approach to classification. By carefully observing a quadrilateral’s properties, such as the length of its sides, the presence of right angles, and the parallelism of its sides, we can accurately identify its type. This process, when honed through practice and problem-solving, empowers us to confidently categorize quadrilaterals and unlock their geometric secrets.

Understanding quadrilaterals extends beyond mere geometric knowledge; it forms the foundation for solving complex geometrical problems and tackling real-world applications. From architecture to engineering, quadrilaterals play a pivotal role in shaping our built environment and facilitating technological advancements. A thorough grasp of their properties and classification enables us to harness their potential and unlock their boundless possibilities.

Types of Quadrilaterals

• Rectangle: Definition, characteristics, and properties
• Parallelogram: Definition, characteristics, and properties
• Rhombus: Definition, characteristics, and properties
• Square: Definition, characteristics, and properties as a special quadrilateral
• Trapezoid: Definition and characteristics
• Kite: Definition and characteristics
• Deltoid: Definition and characteristics

Types of Quadrilaterals

Embark on a geometric expedition as we delve into the captivating world of quadrilaterals, polygons with four tantalizing sides! Characterized by their mesmerizing shapes and intricate properties, quadrilaterals hold a significant place in the realm of geometry, shaping our understanding of the world around us.

Among the captivating family of quadrilaterals lies an enchanting quartet of shapes: rectangles, parallelograms, rhombuses, and squares. Each possesses a unique persona, unlocking a treasure trove of properties that set them apart.

Rectangles: Graceful and symmetrical, rectangles boast four right angles, opposite sides that are congruent, and _parallel sides that create a harmonious dance of lines. Their elegance extends to their area formula: length x width, a simple yet powerful equation that unveils their hidden secrets.

Parallelograms: Slightly less rigid but equally charming, parallelograms enchant with their two pairs of parallel sides that create a sense of balance. They share the alluring property of opposite sides being congruent, but their angles are not restricted to right angles. Like a chameleon, parallelograms can adapt their forms, transitioning into rectangles when their angles align perfectly.

Rhombuses: A tantalizing enigma, rhombuses boast four congruent sides that radiate symmetry. They possess the captivating traits of parallelograms, but with an added dash of allure: all four angles are equal. Rhombuses are the epitome of geometric harmony, where sides and angles harmonize in a mesmerizing dance.

Squares: The golden child of the quadrilateral family, squares excel with four congruent sides and four right angles, making them the ultimate symbol of geometric perfection. They embody the essence of rectangles and rhombuses, merging their captivating qualities to create a shape of unparalleled elegance. Like a jewel in a geometric crown, squares reign supreme in the quadrilateral realm.

**Identifying and Classifying Quadrilaterals: Unraveling the Secrets of Geometric Shapes**

In the realm of geometry, quadrilaterals reign supreme as four-sided polygons that captivate mathematicans and students alike. Navigating the diverse landscape of quadrilaterals requires a keen eye and an understanding of their unique properties.

Steps for Accurate Classification

To embark on the journey of quadrilateral classification, the following steps serve as a reliable guide:

• Examine Opposite Sides: Begin by scrutinizing the opposite sides of the quadrilateral. Are they parallel, perpendicular, or a curious mix of both? This initial observation sets the stage for further classification.

• Inspect Diagonals: Shift your attention to the diagonals, those lines that connect opposite vertices. Their length, intersection point, and angles formed within the quadrilateral provide valuable clues about its type.

• Identify Special Properties: Delve into the unique characteristics that distinguish each quadrilateral. Does it possess equal sides, right angles, or perhaps a combination thereof? These special properties narrow down the classification options.

Practice Problems for Mastery

To solidify your understanding, engage in a series of practice problems:

1. Classify a quadrilateral with opposite sides parallel and equal in length.
2. Determine the type of quadrilateral formed when diagonals intersect at right angles.
3. Identify the quadrilateral that has four equal sides and four right angles.

By grappling with these problems, you strengthen your ability to recognize and categorize quadrilaterals with precision.

In conclusion, the proper identification and classification of quadrilaterals are essential for unlocking a world of geometric exploration. Whether you’re a budding mathematician or a geometry enthusiast, understanding the intricacies of these fascinating shapes empowers you to solve problems, unravel puzzles, and appreciate the beauty of mathematics that surrounds us.