Probability In Biology: Understanding Events And Outcomes

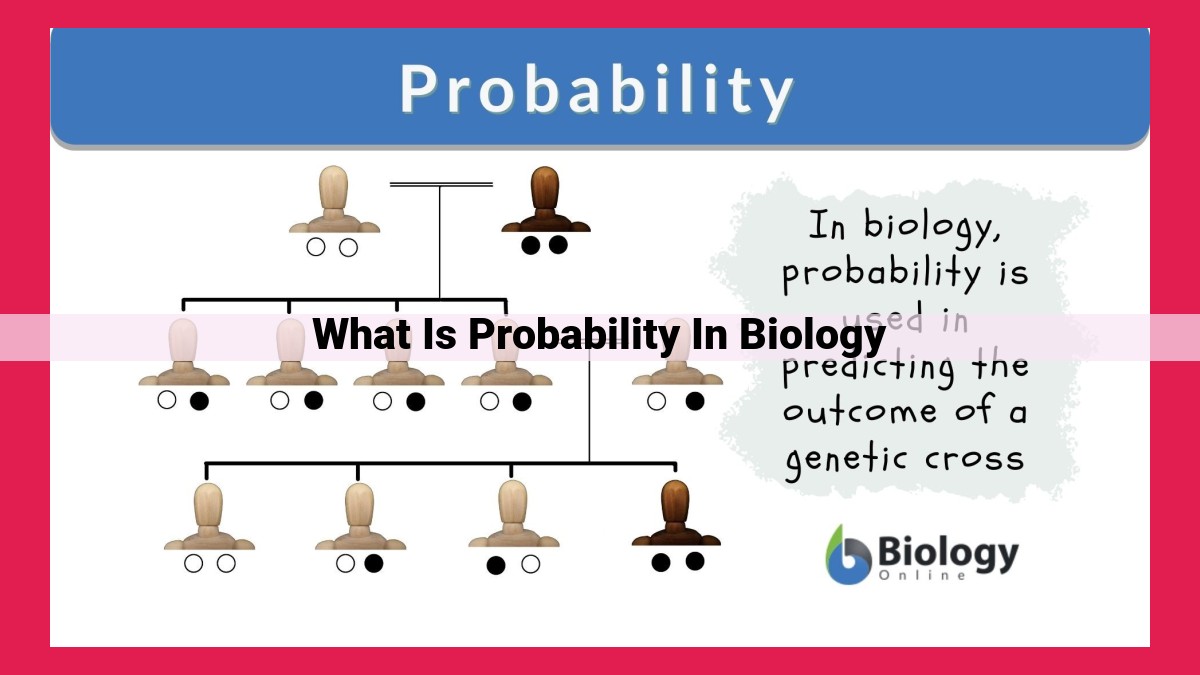
Probability in biology plays a crucial role in understanding the likelihood of events and outcomes in biological systems. It involves concepts like independent and dependent events, where events may influence each other’s probabilities. Tree diagrams and Venn diagrams provide visual representations of probability distributions and overlapping events. Expected value quantifies the average outcome of a probability distribution. These probability principles find applications in various biological fields, including population genetics, ecology, medicine, and bioinformatics.

• What is probability, and why is it important in biology?
• Concepts related to probability, such as independent and dependent events

Probability, the cornerstone of statistics, is the language of uncertainty. It quantifies the likelihood of events occurring and guides our understanding of the biological world’s unpredictable nature.

In biology, probability plays a crucial role in deciphering the patterns of inheritance, predicting disease risks, and modeling complex ecosystems. It allows us to make informed decisions amid uncertainty and infer biological mechanisms from observed outcomes.

Understanding the basic concepts of probability is essential for exploring its applications in biology. Independent events occur without influencing each other, like rolling a dice, while dependent events influence each other’s probability, like drawing a second card from a deck after drawing the first. These concepts pave the way for exploring probability’s versatile tools, such as tree diagrams and Venn diagrams, which visualize the dance of chance.

Visualizing Probability: Tree Diagrams

• What is a tree diagram?
• How to use tree diagrams to represent probabilities and outcomes

Visualizing Probability: Unraveling Outcomes with Tree Diagrams

Imagine tossing a coin. Tails or heads? The outcome is uncertain, but we can visualize the possibilities using a tree diagram.

What is a Tree Diagram?

A tree diagram is a visual representation of probability. It resembles a tree with branches extending from a starting point (root node). Each branch represents a possible outcome, and its length or thickness corresponds to the likelihood of that outcome.

Using Tree Diagrams to Uncover Outcomes

Let’s use a tree diagram to explore the coin toss example. The root node represents the initial toss. From here, two branches extend: one for heads and one for tails. Each branch represents a 50% chance of occurrence.

If we add another toss, the tree branches further. From the heads node, another two branches extend, representing the second toss’s outcome. Similarly, from the tails node, two branches fork out. The end of each branch represents a specific sequence of outcomes.

For instance, one branch may lead to (T, T), indicating two consecutive tails. The probability of this outcome is the combined probability of each individual outcome along the path, in this case, 25% (50% x 50%).

Tree diagrams provide a powerful tool to visualize the probability of multiple events. By tracing the branches, we can deduce all possible outcomes and their corresponding probabilities. This technique is particularly valuable in complex scenarios with numerous outcomes.

In biology, tree diagrams find applications in various areas, including:

• Population genetics: Predicting trait inheritance patterns
• Ecology: Estimating species distribution and abundance
• Medicine: Assessing disease risks and treatment effectiveness

By harnessing the power of tree diagrams, we gain insights into the uncertainty and variability inherent in biological systems. It empowers us to visualize probabilities and make informed decisions amidst the myriad possibilities that nature presents.

Representing Relationships Using Venn Diagrams

In the realm of probability, visualizing relationships and events can be crucial for understanding complex outcomes. One powerful tool for this is the Venn diagram, named after the mathematician John Venn.

What is a Venn Diagram?

A Venn diagram is a graphical representation that uses intersecting circles to illustrate the relationships between different sets. Each circle represents a different set of elements or outcomes, and the area where the circles overlap indicates the intersection or overlap of these sets.

How to Use Venn Diagrams in Probability

Venn diagrams can be particularly useful in biology to illustrate the probability of overlapping events. For example, imagine a study that examines the relationship between plant species found in two different habitats, Habitat A and Habitat B.

The circles in the Venn diagram would represent the set of plant species found in Habitat A (circle A) and the set of plant species found in Habitat B (circle B). The overlapping area would represent the set of plant species that are found in both habitats.

By shading or coloring the different sections of the Venn diagram, we can visualize the probabilities of various outcomes. For instance, the probability of finding a plant species that is present in Habitat A but not in Habitat B can be represented by the area in circle A that is not shaded by circle B.

Venn diagrams provide a simple and intuitive way to understand the probabilities of overlapping events. They are particularly useful in biological contexts where it is necessary to analyze the relationships between different groups, populations, or treatments.

Expected Value: The Average Outcome

Probability theory provides us with a way to predict the likely outcomes of events based on the probability of those outcomes. But what if we’re not just interested in individual outcomes? What if we want to know the average outcome of a random event or experiment? That’s where expected value comes in.

What is Expected Value?

Expected value, also known as mean, is a weighted average of all possible outcomes of an event or experiment, where the weights are the probabilities of each outcome. In other words, it’s the average value of the random variable we’re considering.

How to Calculate Expected Value

To calculate expected value, we multiply each possible outcome by its probability and then add up the results. If we have a random variable X with possible outcomes x₁, x₂, … xₙ and probabilities p₁, p₂, … pₙ, the expected value E(X) is given by:

E(X) = x₁p₁ + x₂p₂ + ... + xₙpₙ

Significance of Expected Value

Expected value is a crucial concept in probability distributions. It tells us the average outcome we can expect from a given experiment or event. It’s particularly important when dealing with random variables that can take on both positive and negative values. For example, in a game of chance, the expected value tells us the average amount of money we can expect to win or lose.

Applications of Expected Value in Biology

• Population Genetics: Expected value is used to predict the probability of inheriting certain traits in offspring.

• Ecology: It helps estimate species abundance and distribution patterns by predicting the average number of individuals in a given habitat.

• Medicine: Expected value aids in assessing disease risk and treatment effectiveness by calculating the average likelihood of developing or responding to a treatment.

Applications of Probability in Biology: Unlocking the Uncertainties

Probability, a fundamental concept in mathematics, plays a pivotal role in various biological disciplines, allowing scientists to grapple with uncertainties and predict outcomes. Here are some key applications of probability in biology:

Population Genetics: The Dance of Inheritance

Population genetics utilizes probability to decipher the patterns of genetic inheritance and predict evolutionary trajectories. By studying the probabilities of allele combinations and gene frequencies, researchers can unravel the forces shaping genetic diversity within populations. This knowledge informs our understanding of evolutionary processes, such as natural selection and genetic drift.

Ecology: Unveiling the Secrets of Abundance and Distribution

In ecology, probability aids in estimating species abundance and distribution patterns. By employing sampling techniques and statistical models, ecologists can determine the likelihood of encountering a species in a particular habitat or region. This information helps in conservation efforts, species management, and predicting the impact of environmental changes on biodiversity.

Medicine: Navigating the Labyrinth of Risk and Treatment

Probability is an indispensable tool in the medical field. It enables physicians to assess the risk of developing diseases based on factors such as genetics, lifestyle, and medical history. Moreover, probability assists in evaluating the effectiveness of medical treatments by determining the likelihood of positive outcomes and adverse effects.

Bioinformatics: Unraveling the Tapestry of Genetic Data

Bioinformatics leverages probability to analyze vast genetic datasets. By employing probabilistic models, researchers can identify patterns and relationships within DNA sequences, predict gene functions, and study the genetic basis of complex diseases. This knowledge contributes to the development of personalized medicine and the understanding of genetic disorders.

Probability provides a powerful lens through which biologists can illuminate the uncertainties inherent in living systems. By unraveling the complexities of genetic inheritance, predicting ecological patterns, assessing medical risks, and deciphering genetic data, probability empowers biologists to make informed decisions and advance our understanding of the biological world.