Master Polynomial Roots: Constructing Polynomials From Zeros

Understanding polynomial roots, using the Factor Theorem, Synthetic Division, and Remainder Theorem enables finding a polynomial with given zeros. By expressing factors as zeroes, synthetically dividing to remove factors, and evaluating at zeroes, one can construct the polynomial. Advanced techniques involving Polynomial Division, Complex Conjugates, and the Quadratic Formula address complex roots. Polynomial roots find applications in solving equations, modeling phenomena, and graph theory, showcasing their importance in various fields.

Understanding the Roots of Polynomials: A Journey into the World of Equations

In the realm of mathematics, there lies an enigmatic world where equations hold the key to unlocking secrets. Among these equations, polynomials reign supreme, their enigmatic roots holding profound implications in various fields. Let’s embark on a storytelling adventure to explore the fascinating world of polynomial roots, unravelling their significance and uncovering the techniques to conquer them.

The Fundamental Pillars of Polynomial Roots

At the heart of polynomial roots lies the Fundamental Theorem of Algebra, which proclaims that every non-constant polynomial with real or complex coefficients can be expressed as the product of linear factors of the form (x - c), where c represents the roots of the polynomial. This theorem serves as the bedrock upon which our understanding of polynomial roots rests.

Complementing this theorem, we define the zeroes of a polynomial as the values of x that make the polynomial equal to zero. These zeroes, akin to hidden treasures, hold crucial information about the polynomial’s behavior and its interactions with the Cartesian plane.

Unveiling Polynomials from Zeros

Armed with our understanding of zeroes, we can now embark on a quest to uncover the secrets of polynomials. The Factor Theorem emerges as our trusty companion, revealing that if a is a zero of the polynomial f(x), then (x - a) is a factor of f(x). This theorem grants us the power to express polynomials in terms of their zeroes.

To simplify the factorization process, we employ the art of Synthetic Division. This technique, likened to a mathematical shortcut, swiftly divides a polynomial by (x - a), providing the quotient and remainder with utmost ease.

Moreover, the Remainder Theorem graces us with the ability to evaluate polynomials at specific values of x. By plugging in a given value into the polynomial and performing division, we can ascertain the remainder without delving into complex calculations.

Finding Polynomials from Scratch: A Step-by-Step Blueprint

In the intriguing world of mathematics, polynomials play a pivotal role, much like the building blocks of our algebraic structures. They wield the power to represent real-world phenomena, pave the way for solving complex equations, and even reveal insights in the intricate field of graph theory. But what if we crave the ability to create these polynomials ourselves, armed with nothing more than their elusive roots?

Enter the Factor Theorem—a fundamental tool that unravels the secret behind constructing polynomials based on their zeros. Simply put, this theorem states that if c is a zero of a polynomial p(x), then x – c is a factor of p(x). This observation becomes our gateway to unlocking the polynomial’s identity.

To put the Factor Theorem into action, we employ a clever technique known as Synthetic Division. It’s an efficient shortcut that streamlines the process of polynomial factorization, often saving us from the laborious long division method. Synthetic Division allows us to swiftly determine whether a given polynomial has a particular root, and if so, it reveals the quotient polynomial—a simplified form that captures the essence of the original polynomial without the zero factor.

But our exploration doesn’t end there. The Remainder Theorem steps into the spotlight, providing a different kind of utility. It asserts that when a polynomial p(x) is divided by x – a, the remainder is precisely p(a). This property empowers us to swiftly evaluate polynomials at specific values of x without delving into the entire division process.

With these three theorems as our guiding stars, we can embark on the thrilling quest of constructing polynomials from scratch. Let’s embark on a step-by-step journey to unveil the magic:

1. Gather Your Zeros: Begin by collecting the zeros of the polynomial you wish to create. These zeros represent the values of x that make the polynomial equal to zero.

2. Factor Your Zeros: Apply the Factor Theorem to each zero, creating a corresponding factor x – c for every zero c.

3. Multiply the Factors: Combine the factors obtained in Step 2 by multiplying them together. This yields the polynomial p(x) that possesses the given zeros.

4. Verify Your Creation: Once you have your polynomial, substitute the zeros back into it to ensure they all produce a value of zero. This serves as a final check to confirm the accuracy of your construction.

Remember, the Factor Theorem, Synthetic Division, and Remainder Theorem form our trusty toolkit in this polynomial-building adventure. Together, they empower us to craft polynomials with precision, unlocking the secrets hidden within their zeros.

Finding a Polynomial with Given Zeros: A Step-by-Step Guide

In the world of polynomials, finding roots or zeros is a crucial skill. And when you’re given a set of zeros, you can use them to construct the polynomial itself. Let’s delve into a step-by-step process that will help you master this art.

Step 1: Understanding the Factor Theorem

The Factor Theorem states that every zero of a polynomial is a factor of that polynomial. In other words, if a polynomial has a zero at x = a, then x – a will be a factor of the polynomial.

Step 2: Using Synthetic Division

Now comes the fun part where you can use synthetic division to factor the polynomial. Using the given zeros, create factors like (x – a), (x – b), and so on. Divide the polynomial by these factors to obtain a quotient polynomial.

Step 3: Applying the Remainder Theorem

The Remainder Theorem tells us that when a polynomial is divided by (x – a), the remainder is equal to f(a), the value of the polynomial at x = a. Use this theorem to determine the constant term of the quotient polynomial, which will be the product of the given zeros with a negative sign.

Step 4: Constructing the Polynomial

Finally, multiply the quotient polynomial by (x – a), (x – b), and so on, for all the given zeros. The product of these factors will be the polynomial with the given zeros.

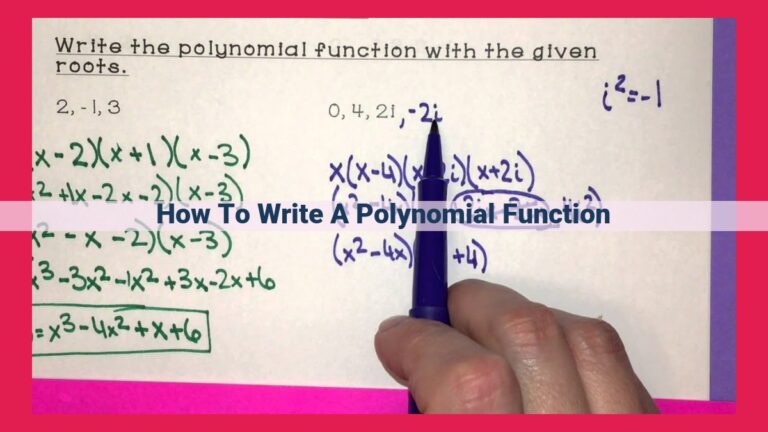
Example

Let’s say you have the zeros x = 2, x = -1, and x = 3.

• Using the Factor Theorem, we have the factors (x – 2), (x + 1), and (x – 3).
• Synthetic division gives us a quotient polynomial of x^2 – 2x + 5.
• The Remainder Theorem confirms that the constant term, -10, is the product of the zeros with a negative sign.
• Multiplying the factors, we get the polynomial f(x) = (x – 2)(x + 1)(x – 3) = x^3 – 4x^2 – 5x + 6.

And there you have it! You’ve successfully constructed a polynomial with the given zeros using the Factor Theorem, Synthetic Division, and Remainder Theorem. Now, go forth and conquer the polynomial world with confidence!

Advanced Techniques for Complex Roots:

• Discuss Polynomial Division for finding roots that are not real numbers.
• Explain the use of Complex Conjugates and the Quadratic Formula for handling complex roots.

Advanced Techniques for Complex Roots

When dealing with polynomials, we often encounter roots that reside beyond the realm of real numbers. These complex roots, expressed as a + bi where a and b are real numbers and _i represents the imaginary unit, require advanced techniques for their discovery.

Polynomial Division

Polynomial division, like a skilled detective, uncovers hidden roots that evade simple methods. It involves dividing one polynomial by another, revealing the roots of the divisor within the quotient. By carefully analyzing the coefficients and constants in this process, we can identify complex roots that may have otherwise remained elusive.

Complex Conjugates and the Quadratic Formula

Complex roots often come in harmonious pairs called complex conjugates. Their symmetry makes them amenable to the Quadratic Formula, a venerable tool for solving quadratic equations. By substituting a complex root and its conjugate into the formula, we can discern the coefficients of the quadratic factor, $(ax^2 + bx + c)$, that corresponds to these complex roots.

Example: Unveiling Complex Roots

Consider the polynomial f(x) = x^3 – 2x^2 + 3x – 4. Using the Factor Theorem, we find that (x-1) is a factor, suggesting that x=1 is a root. Polynomial division reveals the quotient x^2-1, indicating the presence of two additional roots.

Applying the Quadratic Formula to these imaginary roots, we obtain:

x = 1 ± √(-1)
x = 1 ± i

The polynomial f(x) thus has three distinct roots:

x=1, x=1+i, x=1-i

Exploring complex roots unlocks a deeper understanding of polynomial behavior. Polynomial division and the Quadratic Formula serve as powerful weapons in this endeavor, aiding us in unraveling the intricate tapestry of polynomials with roots that dance beyond the boundaries of reality.

Applications of Polynomial Roots:

• Highlight the significance of polynomial roots in various fields, such as solving equations, modeling real-world phenomena, and graph theory.

Applications of Polynomial Roots: Unlocking the Power of Algebra

Beyond their theoretical significance, polynomial roots play a crucial role in diverse fields, from solving equations to modeling real-world phenomena.

Solving Equations: Finding Exact Solutions

Polynomial roots are essential for solving equations. Given an equation of the form p(x) = 0, where p(x) is a polynomial, its roots provide the values of x that satisfy the equation. These roots are the exact solutions to the equation, eliminating the need for approximations.

Modeling Real-World Phenomena: Capturing Complexity

Polynomial roots find application in modeling complex systems in science, engineering, and finance. By approximating real-world data with polynomials, scientists can use their roots to identify patterns and derive insights. For example, polynomial roots can be used to model population growth, predict weather patterns, or analyze financial trends.

Graph Theory: Understanding Network Structures

In graph theory, polynomial roots are used to study the connectivity and properties of networks. The eigenvalues of the adjacency matrix of a graph, which are the roots of its characteristic polynomial, provide information about the graph’s structure and behavior. This knowledge is crucial for optimizing network efficiency, identifying potential bottlenecks, and understanding the flow of information within complex systems.

Polynomial roots are not merely abstract mathematical concepts. They are powerful tools that enable us to solve equations, model real-world phenomena, and analyze complex systems. Their applications span a wide range of fields, empowering us to understand the world in a more precise and comprehensive way.