Master Piecewise Functions: A Comprehensive Guide For Graphing And Understanding

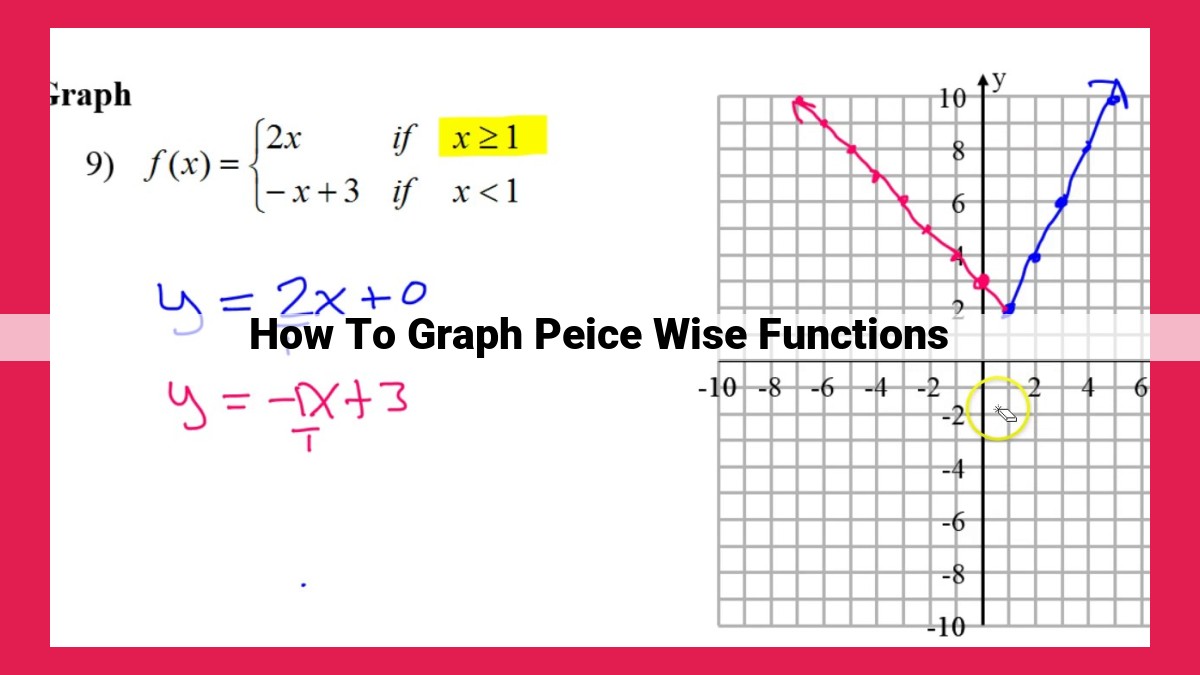
To graph piecewise functions, identify breakpoints and use them to determine intervals where the function is defined differently. For each interval, find the equation that defines the function and plot points to create individual graphs. Connect these graphs at the endpoints of the intervals to form the graph of the piecewise function. Consider whether intervals are open or closed and include any vertical asymptotes where the denominator is zero. By following these steps, you can effectively visualize the behavior of piecewise functions.

• Define piecewise functions and explain why their graphs consist of different pieces.

Unveiling the Secrets of Piecewise Functions: A Journey Through the Puzzle of Segmented Graphs

In the realm of mathematics, there exists a intriguing class of functions known as piecewise functions. These enigmatic entities possess a unique characteristic: their graphs are an intriguing mosaic of distinct pieces, each governed by its own set of rules. Let us embark on a journey to unravel the mysteries of piecewise functions, mastering the art of deciphering their segmented graphs.

Piecewise functions stem from the idea of defining a function differently for distinct intervals on the input domain. Their graphs resemble a patchwork quilt, where each piece represents a different aspect of the function’s behavior. The boundaries between these pieces, known as breakpoints, mark the points where the function’s definition changes.

Understanding piecewise functions requires a keen eye for detail. We must carefully identify the breakpoints and determine the intervals on which the function behaves differently. Each interval is then assigned its own defining equation, which governs the shape and behavior of the graph within that interval.

Next, we embark on the fascinating task of graphing each individual piece of the function. Using our analytical skills and a keen understanding of the equations, we plot points and sketch the graphs on the coordinate plane. It is essential to ensure accuracy in this step, as the individual pieces serve as the building blocks of the overall graph.

Once the individual pieces are in place, the final step is to connect them seamlessly. At the endpoints of each interval, which may be either open or closed, we join the corresponding graphs to form a cohesive whole. This meticulous process results in the complete graph of the piecewise function, a representation of its complex behavior across the entire input domain.

While navigating the world of piecewise functions, we must be mindful of open and closed intervals. Open intervals exclude their endpoints, while closed intervals include them. This distinction profoundly affects the shape of the graph, particularly at the breakpoints.

Finally, we encounter vertical asymptotes, enigmatic entities that arise when the denominator of the function becomes zero. These vertical lines mark points where the function is undefined and its graph approaches infinity or negative infinity. Identifying and graphing vertical asymptotes is crucial for ensuring accuracy and completeness in our piecewise function exploration.

In conclusion, conquering piecewise functions requires a methodical approach that encompasses identifying breakpoints, determining intervals, finding equations, graphing individual pieces, connecting them, and considering open and closed intervals. Mastering these steps empowers us to unravel the intricacies of these segmented graphs, unlocking a deeper understanding of their unique behavior.

Determining Intervals for Each Piece: Navigating the Functional Landscape

In the realm of piecewise functions, the first step towards understanding their intricate graphs is to identify the breakpoints—the points where the function’s definition changes. These breakpoints are like gateways that divide the real number line into intervals, each defined by a distinct equation.

To uncover these crucial breakpoints, we need to scrutinize the given piecewise function carefully. Breakpoints typically occur at points where variables are undefined, such as denominators equal to zero or square roots of negative numbers. They can also emerge at points where the function itself is undefined, like at discontinuities or points of infinite discontinuity.

Once these breakpoints are revealed, we can establish the intervals, which are the stretches of the real number line where the function’s definition remains constant. Each interval is bounded by two breakpoints, and the function’s behavior within that interval is governed by a specific equation.

Identifying Equations for Each Piece: The Key to Piecewise Function Mastery

When it comes to piecewise functions, identifying the equations that define each piece is paramount. These equations are the building blocks upon which the function is constructed, and understanding how they work is essential for mastering the art of graphing them.

Let’s say we have a piecewise function defined as follows:

f(x) = { x + 2, for x ≤ 0
{ 2 - x, for x > 0

Step 1: Identify the Breakpoints

The breakpoints are the points where the function changes its definition. In our case, the breakpoint is x = 0.

Step 2: Determine the Intervals

The intervals are the ranges of x-values for which a particular equation applies. For our function, we have two intervals: (-∞, 0] and (0, ∞).

Step 3: Find the Equations

Now, we need to find the equations that define the function on each interval. For the first interval, x ≤ 0, the equation is:

f(x) = x + 2

For the second interval, x > 0, the equation is:

f(x) = 2 - x

These equations represent the individual pieces of the piecewise function.

Understanding these equations is crucial because they determine the shape and behavior of the graph in each interval. For instance, the first equation f(x) = x + 2 represents a straight line with a slope of 1 and a y-intercept of 2. The second equation f(x) = 2 – x represents a straight line with a slope of -1 and a y-intercept of 2.

Graphing Individual Pieces of Piecewise Functions

When graphing a piecewise function, it’s essential to break it down into its individual pieces. These pieces represent different parts of the function that are defined over specific intervals.

To graph each piece, follow these steps:

1. Plot Points Within the Interval: Choose several x-values within the interval of the piece.

2. Evaluate the Function for Each x-value: Substitute each x-value into the equation defining the piece to find the corresponding y-value.

3. Plot the Points on the Coordinate Plane: Plot the (x, y) pairs generated in step 2 on the coordinate plane.

4. Connect the Points: Use a straight line or curve, depending on the nature of the function, to connect the plotted points. This creates the graph of the piece over the specified interval.

By repeating this process for each piece of the piecewise function, you will obtain multiple graphs that represent the different parts of the function.

Connecting the Pieces: Completing the Graph of a Piecewise Function

We’re almost there! Now that we’ve plotted the individual pieces of our piecewise function, it’s time to connect them to create a complete and cohesive graph.

Think of it like connecting the dots in a drawing. Each dot represents a point on one of the pieces, and our goal is to join them seamlessly to reveal the overall shape of the function.

At the endpoints of each interval, where the pieces meet, we need to decide how to “glue” them together. This is where open and closed intervals come into play.

Open Interval: A gap exists at the endpoint. We represent this with a small circle, indicating that the function does not include the endpoint in its graph.

Closed Interval: No gap exists at the endpoint. We use a solid dot to show that the function includes the endpoint in its graph.

To connect the pieces, we follow these simple rules:

• For open intervals, leave a small space between the endpoint of the first piece and the starting point of the next.
• For closed intervals, connect the endpoint of the first piece directly to the starting point of the next.

By carefully following these rules, we can join the individual pieces of our piecewise function into a complete and accurate graph. This graph will visually represent the function’s behavior over the entire domain, providing a valuable tool for understanding and analyzing its properties.

Consideration of Open and Closed Intervals in Piecewise Functions

When graphing piecewise functions, understanding the difference between open and closed intervals is crucial. Open intervals do not include their endpoints, while closed intervals do. This distinction affects how we graph the function at these endpoints.

Open Intervals:

If a function is defined on an open interval (a, b), we represent the endpoint as an open circle on the graph. This indicates that the function does not take that value at the endpoint. For example, the function f(x) = x² on the interval (0, 1) would be graphed with an empty circle at x = 0 and x = 1.

Closed Intervals:

In contrast, when a function is defined on a closed interval [a, b], we plot the endpoint as a solid circle. This means that the function takes that value at the endpoint. For instance, the function g(x) = |x| on the interval [0, 1] would have a solid circle at both x = 0 and x = 1.

Implications for Graphing:

When joining the individual graphs of a piecewise function at the endpoints of the intervals, the type of interval (open or closed) determines whether the line connects or not.

• Open Intervals: The line does not connect to the endpoint. This creates a small gap at the endpoint, as seen in the case of the function f(x) = x² on (0, 1).
• Closed Intervals: The line does connect to the endpoint. This results in a continuous line passing through the endpoint, as shown for the function g(x) = |x| on [0, 1].

Understanding these interval types is vital for accurately graphing piecewise functions and avoiding errors in representation.

Handling Vertical Asymptotes in Piecewise Functions

Piecewise functions, like complex puzzles, often have hidden challenges that can stump even the most experienced graphers. One such challenge is the presence of vertical asymptotes, which can arise when the function’s denominator drops to zero.

Identifying Vertical Asymptotes

To identify vertical asymptotes, mathematicians employ a simple yet powerful trick: they set the denominator of the function equal to zero and solve for x. The values of x obtained represent the points where the denominator vanishes, creating an infinite jump in the graph.

Graphing Vertical Asymptotes

Once the vertical asymptotes are identified, it’s time to draw them on the coordinate plane. Vertical asymptotes are represented as dotted vertical lines that stretch indefinitely upward and downward. They do not actually touch the graph, but they act as boundaries beyond which the function’s value becomes undefined.

Example: A Function with a Vertical Asymptote

Consider the piecewise function:

f(x) = { 2x + 1, x < 3
       { 1 / (x - 3), x >= 3

For the second piece, setting the denominator equal to zero gives:

x - 3 = 0
x = 3

Thus, x = 3 is the vertical asymptote. When graphing the function, a vertical dotted line is drawn at x = 3, indicating that the graph becomes undefined at this point.

Mastering the art of handling vertical asymptotes is crucial for accurately graphing piecewise functions. By understanding how to identify and draw these boundaries, graphers can unlock the secrets of these intricate mathematical puzzles and create graphs that accurately represent the underlying function.