Unlocking The Mysteries Of ‘P’ In Parabolas: A Comprehensive Guide

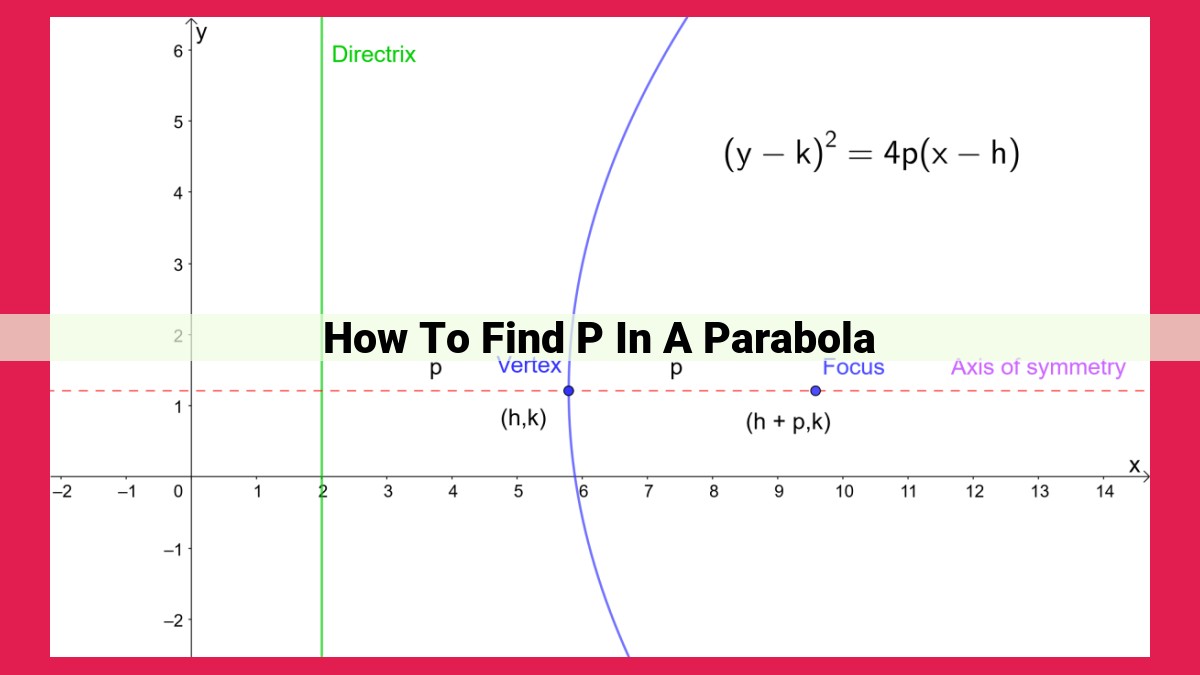
To find the value of p in a parabola, identify the axis of symmetry (vertical line dividing the parabola equally). The distance from the vertex to this axis is p. Alternatively, locate the directrix (horizontal line parallel to the line of symmetry). The distance from the vertex to the directrix is also equal to p. Understanding p provides insights into the shape of the parabola, including the placement of the focus and the opening direction of the parabola.

Unveiling the Secrets of Parabolas: A Journey to Understanding Shape and Form

Parabolas, with their graceful curves and symmetrical forms, are fundamental in mathematics and the world around us. From the trajectory of a thrown ball to the reflectors in headlights, parabolas play a crucial role in understanding motion, light, and countless other phenomena. At the heart of every parabola lies a mysterious parameter known as p, revealing the key to unlocking the secrets of these fascinating curves.

Vertex Form: The Foundation of Parabolas

The vertex form of a parabola is a representation that captures its essential features. It takes the form y = a(x – h)² + k, where (h, k) is the vertex, the point of symmetry. The axis of symmetry, a vertical line passing through the vertex, is given by x = h. The line of symmetry, a horizontal line halfway between the maximum and minimum points of the parabola, is represented by y = k + a/4.

Finding p: A Key to Understanding Parabolas

The value of p provides vital information about the parabola. It represents the distance between the vertex and the focus, a point on the axis of symmetry from which rays parallel to the axis of symmetry reflect toward the parabola. It also represents the distance between the vertex and the directrix, a horizontal line perpendicular to the axis of symmetry that lies p units away from the focus.

Understanding parabolas and the significance of p is essential for deciphering their shape and behavior. Through formulas and geometric relationships, we can precisely determine p, granting us insights into the parabolic world. Whether you’re studying projectile motion, designing reflectors, or simply appreciating the beauty of these curves, unlocking the secrets of parabolas empowers you with a deeper understanding of the mathematical and physical world.

Vertex Form: The Cornerstone of Parabolas

In the realm of mathematics, parabolas hold a captivating allure, their graceful curves reflecting a delicate balance between shape and function. At the heart of every parabola lies the vertex form, the foundation that unlocks the secrets of these enigmatic curves.

The vertex form of a parabola takes the following elegant shape:

y = a(x - h)² + k

Here, the vertex, a crucial point that divides the parabola into two symmetrical halves, takes center stage. The coordinates of this key point are represented by (h, k). Imagine the vertex as the apex of a tent, where the canvas gracefully slopes downward on either side.

Through the vertex, an invisible axis of symmetry bisects the parabola, dividing it into mirror images. This vertical line acts as a central backbone, ensuring that points on one side of the parabola are reflected on the other.

Complementing the axis of symmetry, a line of symmetry emerges, marking the halfway point between the highest and lowest points of the parabola. This horizontal line provides a stable base for the curve, ensuring its equilibrium.

Axis of Symmetry: A Line of Balance

In the realm of parabolas, there exists a crucial line of symmetry like a divider that cleaves the curve into two perfectly mirrored halves. This magical line stands as a vertical sentinel, bisecting the parabola into two congruent regions.

Think of it as a guiding path that splits the parabola down the middle, granting each side an equal share of its distinctive shape. Points that lie at equal distances from this axis of symmetry on opposite sides of the parabola are destined to be twins—identical in both height and curvature.

Visualize this axis as a conductor’s baton, orchestrating the parabola’s graceful dance. It ensures that each point on one side finds its perfect reflection on the other, creating a mesmerizing balance and harmony. The axis of symmetry not only divides the parabola but also unifies it, forging a single, cohesive entity from two seemingly separate halves.

It serves as a defining characteristic of parabolas, a fundamental landmark that shapes their identity. By understanding the axis of symmetry, you gain a deeper appreciation for the intrinsic beauty and intriguing nature of these fascinating curves.

Line of Symmetry: A Horizontal Guide to Unveiling Parabolic Secrets

In the realm of parabolas, the line of symmetry holds a crucial role as a celestial equator, dividing this enigmatic curve into two symmetrical halves, each mirroring the other like celestial twins.

Imagine a parabola, its graceful arc stretching across the expanse of a coordinate plane. Amidst this curved tapestry lies an invisible line that bisects it vertically, acting as a celestial equator for this parabolic domain. This line, known as the line of symmetry, serves as a pivotal guide, revealing hidden patterns and characteristics that shape the parabola’s identity.

Not only does the line of symmetry delineate the parabola’s center, but it also pinpoints the halfway point between its celestial extremes – the maximum and minimum points. It’s like a cosmic yardstick, measuring the equal distances from these peaks and valleys to the line’s unwavering center.

Unveiling the secrets of parabolas hinges upon understanding the significance of their lines of symmetry. By grasping the concept of this horizontal guide, we gain a deeper appreciation for these enigmatic curves and their diverse applications in the world around us.

Focus: The Heart of the Parabola

Imagine a parabola, a graceful curve that arches up like a rainbow or down like an inverted smile. At the heart of this parabola lies a special point, the focus. It’s like the center of the parabola’s world, the point that defines its shape and behavior.

The focus is a point that resides on the axis of symmetry, a vertical line that divides the parabola into two symmetrical halves. It is equally distant from both the vertex, the highest or lowest point of the parabola, and the directrix, a horizontal line that guides the curve’s shape.

Think of the parabola as a mirror. The vertex is the point where incoming rays of light are reflected, and the focus is where those reflected rays converge. The directrix acts like a barrier, preventing the rays from bouncing too far in the opposite direction.

The distance between the vertex and the focus, or between the vertex and the directrix, determines the value of p, a crucial parameter in the equation of a parabola. This value defines the magnitude of the curve, influencing how wide or narrow it is, and how steeply it slopes.

Understanding the focus and its relationship with the other key elements of a parabola is essential for comprehending its behavior and predicting its shape. It’s the focal point that brings the parabola to life, giving it its characteristic curves and guiding its movement.

The Directrix: A Guiding Light in the Realm of Parabolas

As we delve deeper into the enchanting world of parabolas, we encounter another pivotal element – the directrix. Imagine a horizontal line that gracefully glides alongside the line of symmetry, like two celestial dancers in perfect harmony. But what truly sets the directrix apart is its profound connection to the parabola’s enigmatic essence.

The directrix, my fellow explorers, lies at a precise distance of p units from the focus of the parabola. This distance serves as the guiding star, shaping the parabola’s unique curvature and defining its ethereal beauty. In the grand scheme of things, the focus plays the role of a beacon, casting its influence upon every point that adorns the parabola’s mesmerizing curves.

Just as the axis of symmetry bisects the parabola into two mirrored halves, the directrix orchestrates a different kind of symmetry. It divides the parabola into two distinct regions, each harboring points that reflect each other across this enigmatic boundary. This delicate balance adds to the parabola’s allure, making it an object of both mathematical intrigue and aesthetic delight.

So, as we seek to unravel the mysteries of parabolas, let us not forget the profound significance of the directrix. It is a guiding light that leads us to a deeper understanding of these captivating curves, revealing their enchanting secrets and unlocking their hidden treasures of knowledge.

Unveiling the Value of p: A Quest for Parabolic Precision

In the realm of mathematics, parabolas hold a captivating allure, their graceful curves gracing the pages of textbooks and the minds of scholars alike. Understanding the significance of parabolas lies in their ability to model real-world phenomena, such as projectiles, satellites, and even the path of light reflecting from a mirror. At the heart of every parabola lies the enigmatic value of p, a parameter that governs the parabola’s shape and behavior.

Discovering the value of p is an essential step in unlocking the secrets of parabolas. It allows us to pinpoint the parabola’s axis of symmetry, the line that divides it into two mirror-image halves. We can also locate the focus, a pivotal point that determines the parabola’s concentration, and the directrix, a guiding line that ensures the parabola’s graceful curvature.

To embark on this quest for precision, we employ two fundamental formulas:

• Distance between the vertex and the focus: p = (1/4) * (distance between vertex and focus)^2

• Distance between the vertex and the directrix: p = 1/4 * (distance between vertex and directrix)^2

With these formulas in hand, we can navigate the parabolic landscape with confidence, determining the value of p that defines each parabola’s unique characteristics. By understanding the significance of p, we gain a deeper appreciation for the intricate beauty and practical applications of these mathematical marvels.