Determining One-To-One Functions: Essential Techniques And Tests

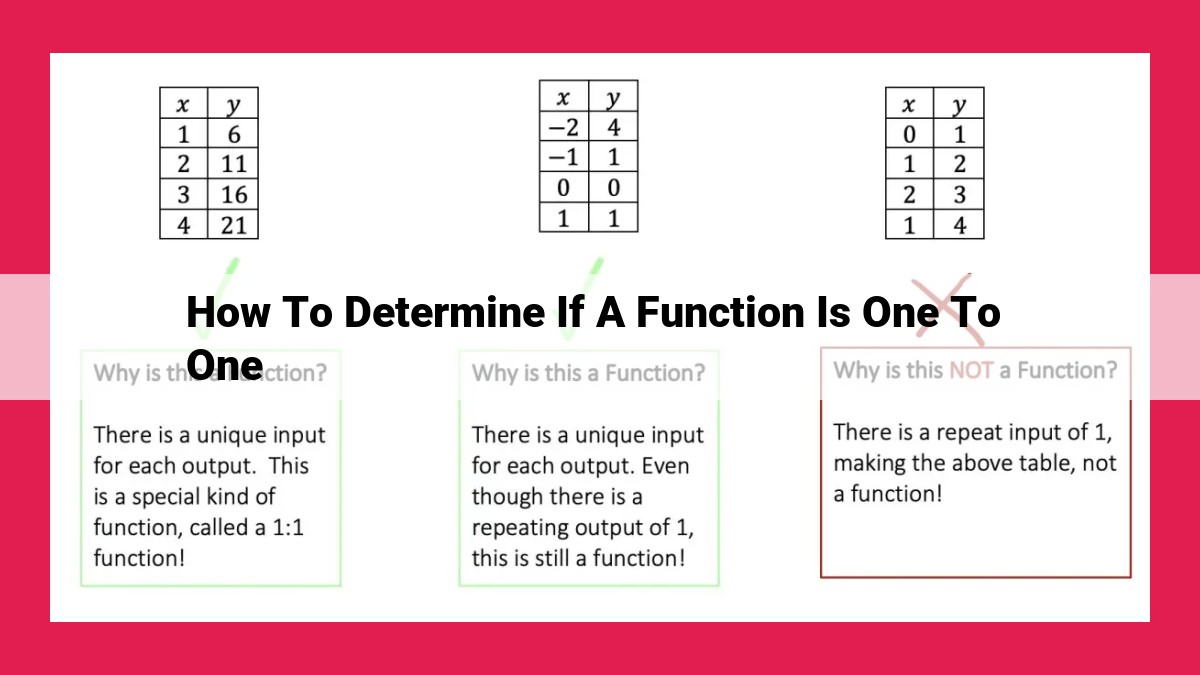
Determining the one-to-one property of a function involves several methods commonly used in mathematics. One approach is the horizontal line test, which checks if any horizontal line intersects the graph of the function more than once. If such an intersection occurs, the function is not one-to-one. Other techniques include the vertical line test, which identifies functions that fail to be one-to-one by detecting vertical asymptotes, and the inverse function test, which establishes a one-to-one relationship if an inverse function exists. Furthermore, the bijection test examines both surjectivity and injectivity to determine one-to-one properties, while the monotonicity test utilizes the concept of increasing or decreasing functions to infer one-to-one relationships. These methods provide a comprehensive toolkit for analyzing the one-to-one property of functions, ensuring accurate and reliable determinations.

Understanding One-to-One Functions: A Journey into Precision and Uniqueness

In the realm of mathematics, one-to-one functions stand as a testament to precision and uniqueness. These exceptional functions possess the remarkable property that for each distinct input, they produce a unique output. Their significance extends far beyond theoretical elegance, playing a vital role in diverse applications, from cryptography to data analysis.

Imagine a function as a magical machine that transforms an input into a corresponding output. One-to-one functions are like meticulous artisans, ensuring that each input emerges as an exclusive masterpiece, never to be replicated by another input. This property guarantees that for any given input, you can trace back to the exact input that produced it, creating a perfect one-to-one correspondence.

In the world of functions, one-to-one relationships are akin to perfectly matched pairs, where each element in the input domain finds its soulmate in the output range, and vice versa. This exclusive bond empowers us to navigate between input and output seamlessly, confident in the knowledge that every step forward or backward leads us to a unique companion.

The Horizontal Line Test: A Simple Way to Detect One-to-One Functions

In the realm of mathematics, one-to-one functions play a crucial role. They establish a unique relationship between inputs and outputs, ensuring that each input corresponds to exactly one output. Identifying these functions is often essential, and here’s where the horizontal line test comes in handy—a simple yet powerful tool that can help you determine if a function is one-to-one or not.

How the Horizontal Line Test Works

Imagine you have a graph of a function. Draw a horizontal line anywhere on the graph. If this line intersects the graph at more than one point, then the function fails the horizontal line test and is not one-to-one. This is because there are different inputs (x-values) that correspond to the same output (y-value), violating the unique input-output relationship.

Conversely, if the horizontal line intersects the graph at only one point, the function passes the horizontal line test and is one-to-one. Each input value has a unique output value, and no two inputs map to the same output.

Examples

• Passing the Test: The function f(x) = x² passes the horizontal line test because any horizontal line will intersect the graph at only one point. For example, the line y = 4 intersects the graph at the point (2, 4) and no other point.

• Failing the Test: The function f(x) = |x| fails the horizontal line test because a horizontal line like y = 2 intersects the graph at two points: (-2, 2) and (2, 2). This indicates that there are two different inputs (-2 and 2) that correspond to the same output (2).

The horizontal line test is a quick and easy way to determine if a function is one-to-one. Simply draw a horizontal line and observe the number of intersection points. If there’s only one intersection for all horizontal lines, the function is one-to-one. By incorporating this test into your mathematical toolkit, you can efficiently identify one-to-one functions and delve deeper into their properties and applications.

The Vertical Line Test: Uncovering Non-One-to-One Relationships in Functions

In mathematics, understanding one-to-one functions is crucial. These functions possess a special property where each input value corresponds to exactly one output value. To determine if a function is one-to-one, we have several tests at our disposal, including the vertical line test.

The vertical line test is a graphical method that helps us identify functions that are not one-to-one. It’s a simple test that relies on drawing vertical lines parallel to the y-axis. If any vertical line intersects the graph of a function at more than one point, the function is not one-to-one.

This is because a one-to-one function must have a unique output value for each input value. If a vertical line intersects the graph at multiple points, it means that the same input value is associated with multiple different output values, violating the one-to-one property.

Vertical Asymptotes

Another important concept related to the vertical line test is vertical asymptotes. These are vertical lines that the graph of a function approaches but never actually touches. The presence of vertical asymptotes in a function’s graph can also indicate a lack of one-to-one relationship.

When a graph has a vertical asymptote, it means that there is a value of x for which the function is undefined. This discontinuity in the function’s graph creates a “hole” where the vertical line cannot intersect the graph. As a result, the function fails the vertical line test and is not one-to-one.

Example

Consider the function f(x) = 1/(x-2). The graph of this function has a vertical asymptote at x=2. If we draw a vertical line parallel to the y-axis anywhere except at x=2, the line will intersect the graph at only one point. However, if we draw a vertical line at x=2, the line will not intersect the graph at all. This indicates that the function is not one-to-one, as a single input value (x=2) is associated with no output value.

The Inverse Function Test: Unlocking One-to-One Relationships

Imagine a world where every lock has only one key that can open it. Similarly, in mathematics, we have functions that exhibit such a unique relationship between inputs and outputs, known as one-to-one functions. The Inverse Function Test provides a powerful tool to unveil these exceptional functions.

The Inverse Function Test proclaims: if a function has an inverse function, then it’s one-to-one. This is akin to saying that for every lock, there exists only one key that can unlock it. An inverse function, denoted as f^-1(x), reverses the input-output relationship, effectively “undoing” the original function.

Consider a function f(x) = 2x + 1. For every input x, f(x) produces a unique output 2x + 1. To check for one-to-oneness using the Inverse Function Test, we attempt to find an inverse function. Solving f(x) for x, we get x = (f(x) – 1) / 2, which defines the inverse function f^-1(x) = (x – 1) / 2.

The existence of the inverse function f^-1(x) proves that f(x) is one-to-one because for every output, there is a unique input that produces it. In other words, every lock has a key, and only one key can unlock it. The inverse function provides the key, ensuring a one-to-one relationship.

The Inverse Function Test is a valuable tool for recognizing functions that exhibit this unique property. By establishing the existence of an inverse function, we can confidently assert that the function under scrutiny is indeed one-to-one.

The Bijection Test: A Gateway to One-to-One Functions

In the realm of functions, many tests can determine a function’s nature and behavior. One such test is the bijection test, a powerful tool in identifying one-to-one functions.

A bijection is a special type of function that is both injective and surjective. Injectivity means that the function assigns different outputs to different inputs. In other words, each input has a unique output. Surjectivity, on the other hand, means that every output of the function is produced by at least one input.

Breaking Down the Bijection Test

To understand how the bijection test works, we must delve into its two components:

1. Injectivity (One-to-One):

A function is injective if, for any two distinct inputs, it produces distinct outputs. A simple way to visualize this is to imagine drawing a horizontal line across the graph of the function. If the line intersects the graph at multiple points, the function is not injective. However, if the line intersects the graph at only one point for each input, the function is indeed injective.

2. Surjectivity (Onto):

A function is surjective if, for every output within its range, there is at least one input that produces that output. In other words, the function’s range covers all possible outputs. A simple trick is to check if the range of the function is equal to its codomain (the set of all possible outputs). If they are equal, the function is surjective.

The Power of Bijection

If a function is both injective and surjective, it meets the criteria for being a bijection. This means that the function is one-to-one, mapping each input to a unique output. The inverse of a bijection is also a bijection, ensuring that the input and output values can be uniquely mapped in both directions.

By utilizing the bijection test, mathematicians can establish a function’s one-to-one nature and gain valuable insights into its properties. This knowledge is essential in various areas of mathematics, including algebra, calculus, and set theory.

So, there you have it: the bijection test, a fundamental tool that unveils the secrets of one-to-one functions. Embrace its power and conquer the world of mathematics with confidence!

**Monotonicity Test: A Foolproof Method to Identify One-to-One Functions**

In mathematics, a one-to-one function, also known as a bijection, possesses a fundamental property that guarantees uniqueness: for every input, it produces a unique output. This concept is crucial for understanding functions and their applications.

One of the most straightforward ways to determine if a function is one-to-one is the monotonicity test. This test capitalizes on the inherent characteristic of strictly increasing or strictly decreasing functions: they are inherently one-to-one.

A strictly increasing function exhibits a pattern where as the input increases, the output also steadily increases without any plateaus or decreases. Conversely, a strictly decreasing function demonstrates a pattern where as the input increases, the output consistently decreases.

The rationale behind the monotonicity test lies in the fact that a strictly increasing or decreasing function cannot generate two identical outputs for different inputs. If that were to happen, it would contradict their strictly increasing or decreasing nature, creating a non-unique input-output relationship.

Therefore, if a function exhibits a strictly increasing or strictly decreasing pattern, it is intrinsically one-to-one. This test provides a simple yet effective approach to identifying one-to-one functions, ensuring that each input is uniquely paired with its corresponding output.