Obtuse Triangle Area Calculation: Heron’s Formula Vs. Law Of Cosines

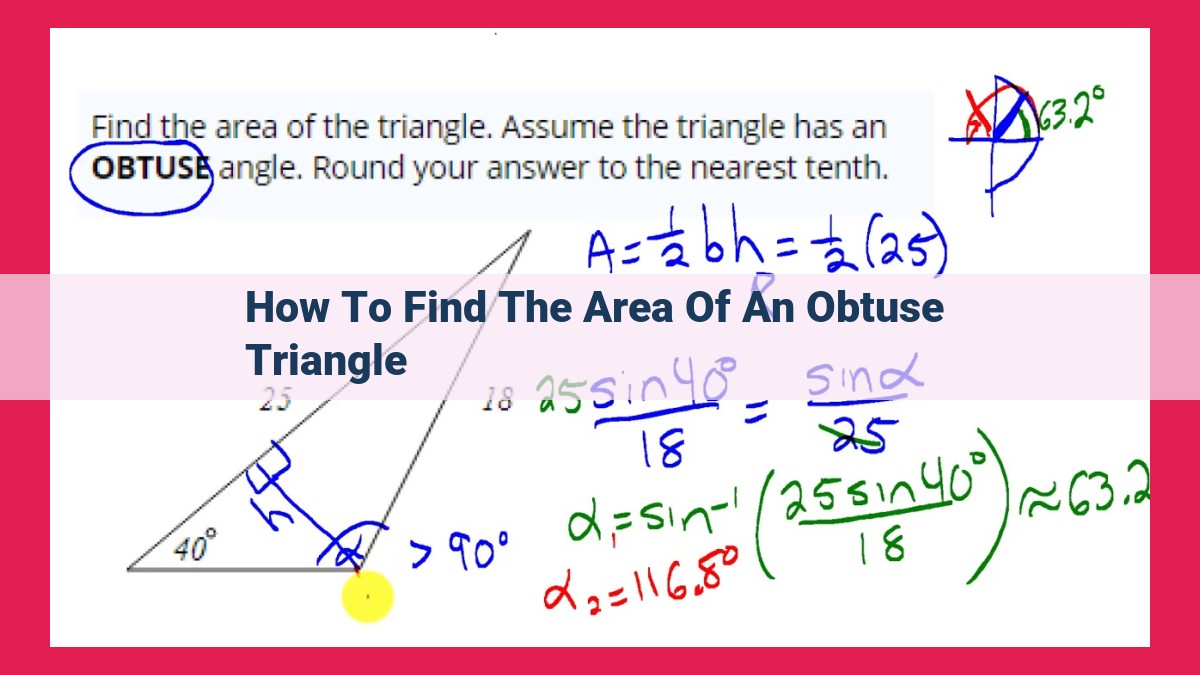
To find the area of an obtuse triangle, you can use Heron’s Formula if all three sides are known, or the Law of Cosines if two sides and the included angle are known. Heron’s Formula involves finding the semiperimeter (half the perimeter) and using it to calculate the area. The Law of Cosines relates the cosine of the included angle to the side lengths, allowing you to determine the area. Understanding the concepts of perimeter and semiperimeter is crucial for accurate calculations.

Navigating the Realm of Triangles: Unlocking the Area of Obtuse Triangles

In the vast world of geometry, triangles reign supreme as the building blocks of countless shapes and structures. Among this diverse family, obtuse triangles stand out with their unique characteristic: one interior angle that measures greater than 90 degrees. While this distinguishing feature sets them apart from their acute and right triangle brethren, it also poses a unique challenge when it comes to calculating their area.

In this comprehensive guide, we’ll embark on a journey into the world of obtuse triangles, unraveling the secrets behind their area calculation. Along the way, we’ll introduce you to the Heron’s Formula and the Law of Cosines, two mathematical tools that hold the key to unlocking the mysteries of these intriguing shapes.

Defining the Enigma: Obtuse Triangles vs. Acute and Right Triangles

Triangles, as you may recall, are defined by their three sides and three interior angles. An obtuse triangle is characterized by one obtuse angle, which is greater than 90 degrees. To put it simply, if you imagine a triangle laid flat on a table, an obtuse angle would be the one that “bulges” out the most.

In contrast, acute triangles have all three angles measuring less than 90 degrees, while right triangles possess one right angle (exactly 90 degrees). This distinction in angles plays a crucial role in determining the area of a triangle, as we shall soon discover.

Finding the Area of Obtuse Triangles: A Journey through Heron’s Formula and the Law of Cosines

In the realm of geometry, triangles reign supreme, each with its unique characteristics. Among them, obtuse triangles stand out with their unique angles, greater than 90 degrees. Understanding the area of these intriguing shapes is crucial, and this guide will take you on an enlightening journey to master the methods of finding the area of obtuse triangles.

Method 1: Heron’s Formula

For triangles with all three sides known, Heron’s Formula provides an elegant solution:

Area = √(s(s - a)(s - b)(s - c))

where:

• s = semiperimeter (half of the perimeter) = (a + b + c) / 2
• a, b, c = lengths of the three sides

Let’s embark on an example. Imagine a triangular garden with sides measuring 8 meters, 10 meters, and 12 meters. Using Heron’s Formula:

s = (8 + 10 + 12) / 2 = 15

Area = √(15(15 - 8)(15 - 10)(15 - 12)) = **48 square meters**

This reveals that the garden covers 48 square meters of lush greenery.

Method 2: Law of Cosines

If you’re given two sides and the included angle, the Law of Cosines comes to the rescue:

Area = 1/2 * a * b * sin(C)

where:

• a, b = lengths of the two known sides
• C = measure of the included angle between sides a and b

Consider a triangle with sides measuring 5 inches and 7 inches, and an included angle of 120 degrees:

Area = 1/2 * 5 * 7 * sin(120°) = **17.5 square inches**

This method proves invaluable when working with triangles that have obtuse angles.

Unraveling the Enigma of Obtuse Triangle Areas

In the realm of geometry, triangles hold a captivating allure, with their intriguing shapes and enigmatic properties. Among these, the obtuse triangle stands apart, boasting an allure that stems from its distinct interior angle. Defined by an angle greater than 90 degrees, the obtuse triangle presents a challenge to mathematicians seeking to determine its area.

To unravel this enigma, we embark on a captivating journey, uncovering the methods that unveil the hidden secrets of obtuse triangle areas. Join us as we delve into Heron’s Formula, a legendary tool that empowers us to calculate the area when all three sides are known. We’ll unravel the mysteries of perimeter and semiperimeter, revealing their crucial roles in this enigmatic equation. Through practical applications, we’ll witness the magic of Heron’s Formula in action.

But our quest doesn’t end there. We’ll venture into the fascinating world of the Law of Cosines, a powerful ally when two sides and the included angle are known. Together, we’ll unravel the intricate relationship between cosine and side lengths, using step-by-step solutions to conquer even the most perplexing of challenges.

Beyond the Equation: Exploring Additional Concepts

Our exploration extends beyond mere formulas, delving into the profound angle and side relationships that shape the geometry of triangles. We’ll uncover the intrinsic connection between acute and obtuse angles, revealing how they influence the triangle’s overall makeup.

Furthermore, we’ll shed light on the crucial concept of perimeter, the sum of all three sides. Its profound significance in Heron’s Formula calculations cannot be overstated. And we’ll delve into the enigmatic world of semiperimeter, a concept that holds the key to unlocking hidden symmetries within the triangle’s geometry.

Embracing the Power of Understanding

As we conclude our journey, we’ll reflect on the significance of understanding these additional concepts. Armed with a holistic perspective, we’ll appreciate the interplay between angles, sides, perimeter, and semiperimeter. This newfound understanding empowers us to approach obtuse triangle area calculations with confidence and precision.

Remember, the true beauty of mathematics lies in its ability to unveil the hidden secrets of our world. Embrace the challenge of conquering obtuse triangle areas, and discover the boundless possibilities that await you within the realm of geometry.